- 2021-06-11 发布 |
- 37.5 KB |
- 5页


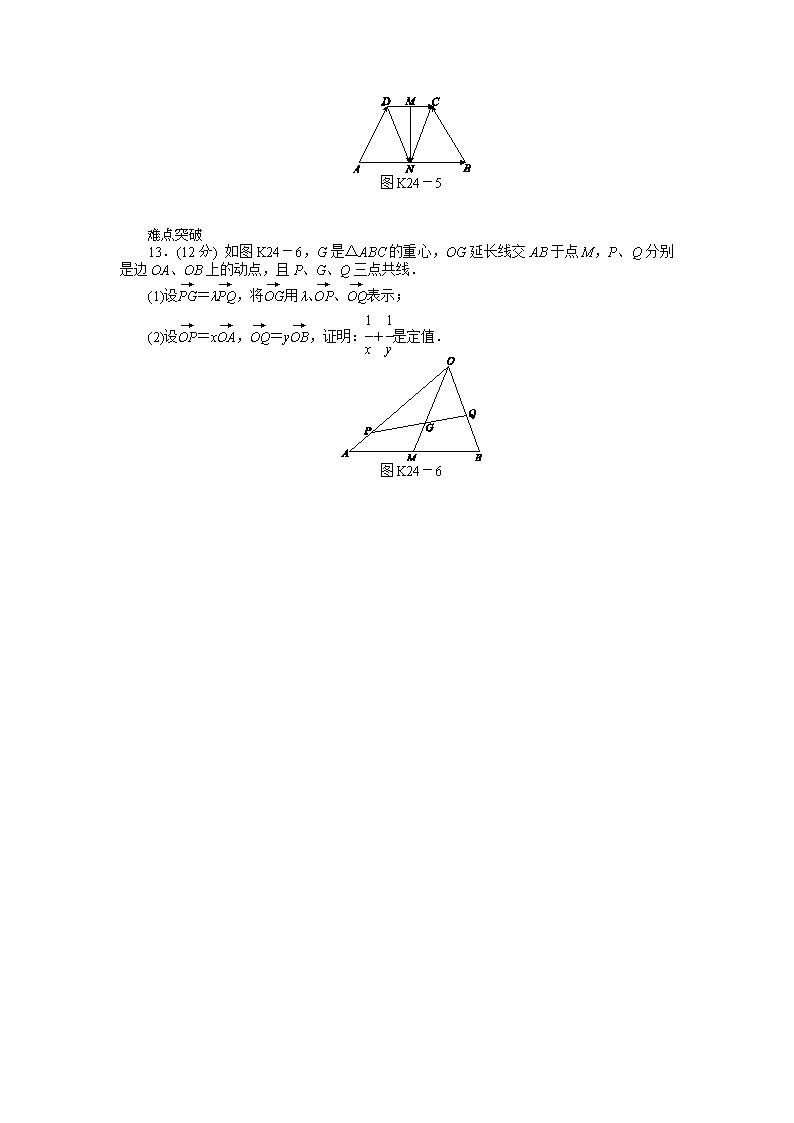
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013届人教A版理科数学课时试题及解析(24)平面向量的概念及其线性运算
课时作业(二十四) [第 24 讲 平面向量的概念及其线性运算] [时间:35 分钟 分值:80 分] 基础热身 1. 如图 K24-1,正六边形 ABCDEF 中,BA→+CD→ +EF→=( ) 图 K24-1 A.0 B.BE→ C.AD→ D.CF→ 2. 设非零向量 a,b,c,若 p= a |a| + b |b| + c |c| ,那么|p|的取值范围为( ) A.[0,1] B.[0,2] C.[0,3] D.[1,2] 3. 已知向量 a=(x,2),b=(3,-1),若(a+b)∥(a-2b),则实数 x 的值为( ) A.-3 B.2 C.4 D.-6 4. 如图 K24-2 所示的方格纸中有定点 O,P,Q,E,F,G,H,则OP→ +OQ→ =( ) 图 K24-2 A.OH→ B.OG→ C.FO→ D.EO→ 能力提升 5.已知λ∈R,则下列命题正确的是( ) A.|λa|=λ|a| B.|λa|=|λ|a C.|λa|=|λ||a| D.|λa|>0 6. △ABC 的三个内角 A、B、C 的对边分别为 a、b、c,已知 sinB=1,向量 p=(a, b),q=(1,2).若 p∥q,则 C 的大小为( ) A.π 6 B.π 3 C.π 2 D.2π 3 7.已知△ABC 和点 M 满足MA→ +MB→ +MC→ =0,若存在实数 m 使得AB→+AC→=m AM→ 成立, 则 m=( ) A.2 B.3 C.4 D.5 8. 如图 K24-3,△ABC 中,AD=DB,AE=EC,CD 与 BE 交于 F.设AB→=a,AC→= b,AF→=xa+yb,则(x,y)为( ) 图 K24-3 A. 1 2 ,1 2 B. 2 3 ,2 3 C. 1 3 ,1 3 D. 2 3 ,1 2 图 K24-4 9. 如图 K24-4,在△ABC 中,AN→=1 3NC→ ,P 是 BN 上的一点,若AP→=mAB→+ 2 11AC→, 则实数 m 的值为________. 10. 若 M 为△ABC 内一点,且满足AM→ =3 4AB→+1 4AC→,则△ABM 与△ABC 的面积之比 为________. 11.设 a、b 为平面向量,若存在不全为零的实数λ,μ使得λa+μb=0,则称 a、b 线性 相关,下面的命题中,a、b、c 均为已知平面 M 上的向量. ①若 a=2b,则 a、b 线性相关; ②若 a、b 为非零向量,且 a⊥b,则 a、b 线性相关; ③若 a、b 线性相关,b、c 线性相关,则 a、c 线性相关; ④向量 a、b 线性相关的充要条件是 a、b 共线. 上述命题中正确的是________(写出所有正确命题的序号) 12.(13 分) 如图 K24-5 所示,若四边形 ABCD 是一个等腰梯形,AB∥DC,M、N 分别是 DC、AB 的中点,已知AB→=a,AD→ =b,DC→ =c,试用 a,b,c 表示BC→,MN→ . 图 K24-5 难点突破 13.(12 分) 如图 K24-6,G 是△ABC 的重心,OG 延长线交 AB 于点 M,P、Q 分别 是边 OA、OB 上的动点,且 P、G、Q 三点共线. (1)设PG→ =λPQ→ ,将OG→ 用λ、OP→ 、OQ→ 表示; (2)设OP→ =xOA→ ,OQ→ =yOB→ ,证明:1 x +1 y 是定值. 图 K24-6 课时作业(二十四) 【基础热身】 1.D [解析] BA→+CD→ +EF→=BA→+AF→-BC→=BF→-BC→=CF→,所以选 D. 2.C [解析] 因为 a |a| ,b |b| , c |c| 是三个单位向量,因此三个向量同向时,|p|的最大值为 3. 3.D [解析] 因为(a+b)∥(a-2b),a+b=(x+3,1),a-2b=(x-6,4), ∴4(x+3)-(x-6)=0,x=-6. 4.C [解析] 设 a=OP→ +OQ→ ,利用平行四边形法则作出向量OP→ +OQ→ ,再平移即发现 a=FO→ . 【能力提升】 5.C [解析] 当λ<0 时,|λa|=λ|a|不成立,A 错误;|λa|应该是一个非负实数,而非向 量,所以 B 不正确;当λ=0 或 a=0 时,|λa|=0,D 错误. 6.B [解析] 由 sinB=1⇒B=π 2 ,在△ABC 中 cosC=a b , 又由 p=(a,b),q=(1,2),p∥q⇒2a-b=0⇒a=b 2 ,故 cosC=1 2 ⇒C=π 3. 7.B [解析] 由题目条件可知,M 为△ABC 的重心,连接 AM 并延长交 BC 于 D, 则AM→ =2 3AD→ ①,因为 AD 为中线,则AB→+AC→=2AD→ =mAM→ , 即 2AD→ =mAM→ ②,联立①②可得 m=3,故 B 正确. 8.C [解析] ∵AD=DB,AE=EC, ∴F 是△ABC 的重心,则DF→ =1 3DC→ , ∴AF→=AD→ +DF→ =AD→ +1 3DC→ =AD→ +1 3(AC→-AD→ ) =2 3AD→ +1 3AC→=1 3AB→+1 3AC→, ∴x=1 3 ,y=1 3. 9. 3 11 [解析] AP→=1 4AC→+NP→=mAB→+ 2 11AC→,NP→=mAB→- 3 44AC→. NB→=NC→ +CB→=3 4AC→+(AB→-AC→)=AB→-1 4AC→,设NP→=λNB→,则λAB→-1 4λAC→=mAB→- 3 44AC→, m=λ= 3 11. 10.1 4 [解析] 由题知 B、M、C 三点共线,设BM→ =λBC→,则:AM→ -AB→=λ(AC→-AB→), ∴AM→ =(1-λ)AB→+λAC→, ∴λ=1 4 , ∴S△ABM S△ABC =1 4. 11.①④ [解析] ②若 a⊥b,则 a、b 不线性相关,命题错误;③b 为零向量时,命题 错误. 12.[解答] BC→=BA→+AD→ +DC→ =-a+b+c, ∵MN→ =MD→ +DA→ +AN→, 又∵MD→ =-1 2DC→ ,DA→ =-AD→ ,AN→=1 2AB→, ∴MN→ =1 2a-b-1 2c. 【难点突破】 13.[解答] (1)OG→ =OP→ +PG→ =OP→ +λPQ→ =OP→ +λ(OQ→ -OP→ )=(1-λ)OP→ +λOQ→ . (2)证明:由(1),得 OG→ =(1-λ)OP→ +λOQ→ =(1-λ)xOA→ +λyOB→ .① ∵G 是△OAB 的垂心, ∴OG→ =2 3OM→ =2 3 ×1 2(OA→ +OB→ )=1 3OA→ +1 3OB→ .② 而OA→ 、OB→ 不共线, ∴由①②,得 1-λx=1 3 , λy=1 3 . 解之,得 1 x =3-3λ, 1 y =3λ, ∴1 x +1 y =3,即1 x +1 y 是定值.查看更多