- 2021-06-11 发布 |
- 37.5 KB |
- 6页


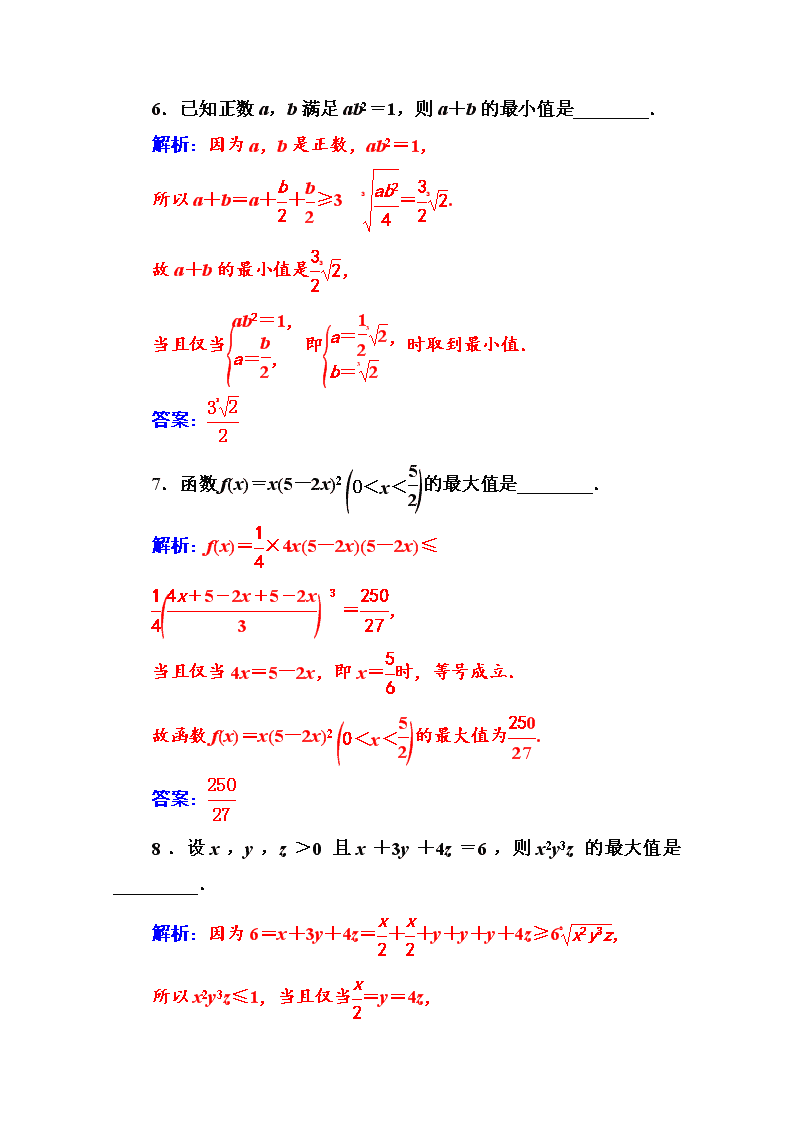
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版高中数学选修4-5练习:第一讲1-1-1-1-3三个正数的算术—几何平均不等式word版含解析
第一讲 不等式和绝对值不等式 1.1 不等式 1.1.3 三个正数的算术—几何平均不等式 A 级 基础巩固 一、选择题 1.若实数 x,y 满足 xy>0,且 x2y=2,则 xy+x2 的最小值是( ) A.1 B.2 C.3 D.4 解 析 : xy + x2 = 1 2 xy + 1 2 xy + x2 ≥ 3 3 1 2xy·1 2xy·x2 = 3 3 1 4 (x2y)2=3 3 4 4 =3,当且仅当 1 2xy=x2,即 x=1 时,等号成立. 答案:C 2.若 a>b>0,则 a+ 1 b(a-b)的最小值为( ) A.0 B.1 C.2 D.3 解析:因为 a+ 1 b(a-b)=(a-b)+b+ 1 b(a-b)≥ 3 3 (a-b)·b· 1 b(a-b)=3,当且仅当 a=2,b=1 时取等号, 所以 a+ 1 b(a-b)的最小值为 3. 答案:D 3.设 x,y,z∈R+,且 x+y+z=6,则 lg x+lg x+lg z 的取值范 围是( ) A.(-∞,lg 6] B.(-∞,3lg 2] C.lg 6,+∞) D.3lg 2,+∞) 解析:因为 lg x+lg y+lg z=lg(xyz), 而 xyz≤ x+y+z 3 3 =23, 所以 lg x+lg y+lg z≤lg 23=3lg 2,当且仅当 x=y=z=2 时,取 等号. 答案:B 4.已知 x+2y+3z=6,则 2x+4y+8z 的最小值为( ) A.33 6 B.2 2 C.12 D. 123 5 解析:2x+4y+8z=2x+22y+23z≥3 3 26=12. 当且仅当 x=2y=3z=2 时等号成立. 答案:C 5.若 logxy=-2,则 x+y 的最小值是( ) A.33 2 2 B.23 3 3 C.3 3 2 D.2 2 3 解析:当 logxy=-2,得 x-2=y,即 x2y=1,且 x>0,y>0, x+y=1 2x+1 2x+y≥3 3 1 2x·1 2x·y=3 2 3 2. 当且仅当 1 2x=y 时等号成立. 答案:A 二、填空题 6.已知正数 a,b 满足 ab2=1,则 a+b 的最小值是________. 解析:因为 a,b 是正数,ab2=1, 所以 a+b=a+b 2 +b 2 ≥3 3 ab2 4 =3 2 3 2. 故 a+b 的最小值是3 2 3 2, 当且仅当 ab2=1, a=b 2 , 即 a=1 2 3 2, b= 3 2 时取到最小值. 答案:3 3 2 2 7.函数 f(x)=x(5-2x)2 0<x<5 2 的最大值是________. 解析:f(x)=1 4 ×4x(5-2x)(5-2x)≤ 1 4 4x+5-2x+5-2x 3 3 =250 27 , 当且仅当 4x=5-2x,即 x=5 6 时,等号成立. 故函数 f(x)=x(5-2x)2 0<x<5 2 的最大值为250 27 . 答案:250 27 8.设 x,y,z>0 且 x+3y+4z=6,则 x2y3z 的最大值是_________. 解析:因为 6=x+3y+4z=x 2 +x 2 +y+y+y+4z≥6 6 x2y3z, 所以 x2y3z≤1,当且仅当x 2 =y=4z, 即 x=2,y=1,z=1 4 时,等号成立. 所以 x2y3z 取得最大值 1. 答案:1 三、解答题 9.θ为锐角,求 y=sin θ·cos2θ的最大值. 解:y2=sin2θcos2θcos2θ=1 2 ·2sin2θ(1-sin2θ)(1-sin2θ)≤1 2 2 3 3 = 4 27. 当且仅当 2sin2θ=1-sin2θ,即 sin θ= 3 3 时取等号. 所以 ymax=2 3 9 . 10.已知 a,b,c 为正数,求证: (a+b+c)(a2+b2+c2)≥9abc. 证明:因为 a,b,c 为正数, 所以 a+b+c≥3 3 abc,a2+b2+c2≥3 3 a2b2c2 所以(a+b+c)(a2+b2+c2)≥3 3 abc·3 3 a2b2c2=9 3 abc·a2b2c2. 所以(a+b+c)(a2+b2+c2)≥9abc, 当且仅当 a=b=c 时等号成立. B 级 能力提升 1.若数列{an}的通项公式是 an= n n3+128 ,则该数列中的最大项是 ( ) A.第 4 项 B.第 6 项 C.第 7 项 D.第 8 项 解析:an= n n3+128 = 1 n2+128 n = 1 n2+64 n +64 n 因为 n2+64 n +64 n ≥3 3 n2·64 n ·64 n =48, 当且仅当 n2=64 n ,即 n=4 时,等号成立, 所以 an≤ 1 48 ,该数列的最大项是第 4 项. 答案:A 2.函数 y=4sin2x·cos x 的最大值为__________,最小值为 ________. 解析:因为 y2=16sin2x·sin2x·cos2x= 8(sin2x·sin2x·2cos2x)≤8 sin2x+sin2x+2cos2x 3 3 =8× 8 27 =64 27 , 所以 y2≤64 27 ,当且仅当 sin2x=2cos2x,即 tan x=± 2时取等号. 所以 ymax=8 9 3,ymin=-8 9 3. 答案:8 3 9 -8 3 9 3.请你设计一个帐篷,它下部的形状是高为 1 m 的正六棱柱,上 部的形状是侧棱长为 3 m 的正六棱锥,如图所示.试问当帐篷的顶点 O 到底面中心 O1 的距离为多少时,帐篷的体积最大? 解:设 OO1 为 x m,则 1<x<4.由题设可得正六棱锥底面边长为 32-(x-1)2= 8+2x-x2,于是底面正六边形的面积为 6× 3 4 × ( 8+2x-x2)2=3 3 2 (8+2x-x2), 帐篷的体积为 V(x)=3 3 2 (8+2x-x2)· 1 3 (x-1)+1 = 3 2 (4-x)(x + 2)(x + 2) = 3 4 (8 - 2x)(x + 2)(x + 2)≤ 3 4 (8-2x)+(x+2)+(x+2) 3 3=16 3. 当且仅当 8-2x=x+2,即 x=2 时取等号. 即当帐篷的顶点 O 到底面中心 O1 的距离为 2 m 时帐篷的体积最 大.查看更多