2020版高中数学 第2章 数列章末分层突破学案 新人教B版必修5
第2章 数列
章末分层突破
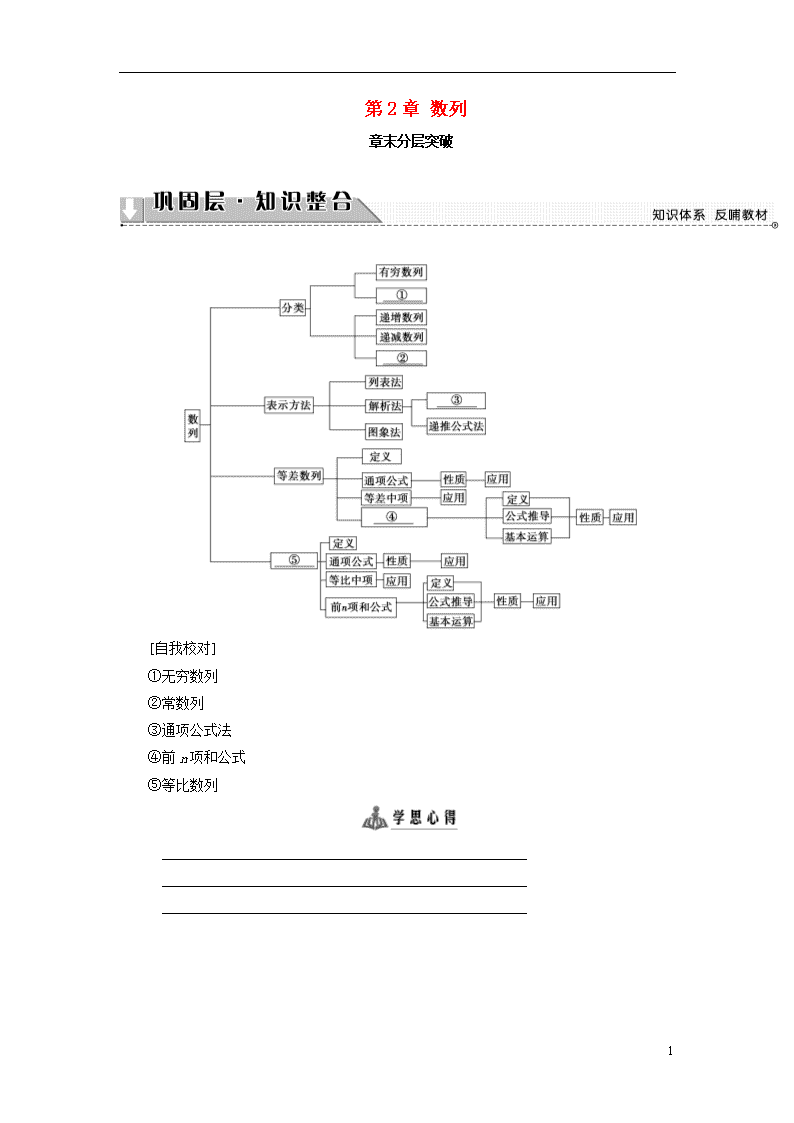
[自我校对]
①无穷数列
②常数列
③通项公式法
④前n项和公式
⑤等比数列
10
等差(比)数列的基本运算
在等差数列和等比数列的通项公式an与前n项和公式Sn中,共涉及五个量:a1,an,n,d(或q),Sn,其中a1和d(或q)为基本量,“知三求二”是指将已知条件转换成关于a1,d(q),an,Sn,n的方程组,利用方程的思想求出需要的量,当然在求解中若能运用等差(比)数列的性质会更好,这样可以化繁为简,减少运算量,同时还要注意整体代入思想方法的运用.
等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式;
(2)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
【精彩点拨】 (1)由a1,a4求出公比q,写出{an}的通项公式.(2)列出关于b1,d的方程组,求解b1,d,进而写出bn,Sn.
【规范解答】 (1)设{an}的公比为q,
由已知得16=2q3,
解得q=2.∴an=2×2n-1=2n.
(2)由(1)得a3=8,a5=32,则b3=8,b5=32.
设{bn}的公差为d,则有
解得
所以bn=-16+12(n-1)=12n-28.
所以数列{bn}的前n项和
Sn==6n2-22n.
[再练一题]
1.已知等差数列{an}的公差d=1,前n项和为Sn.
(1)若1,a1,a3成等比数列,求a1;
(2)若S5>a1a9,求a1的取值范围.
【解】 (1)因为数列{an}的公差d=1,且1,a1,a3成等比数列,所以a=1×(a1+2),
即a-a1-2=0,解得a1=-1或a1=2.
(2)因为数列{an}的公差d=1,且S5>a1a9,
所以5a1+10>a+8a1,
10
即a+3a1-10<0,解得-5
1时,an=Sn-Sn-1=k(cn-cn-1),
则a6=k(c6-c5),a3=k(c3-c2),==c3=8,
∴c=2.
∵a2=4,即k(c2-c1)=4,解得k=2,∴an=2n.
当n=1时,a1=S1=2.
综上所述,an=2n(n∈N+).
(2)nan=n·2n,则Tn=2+2·22+3·23+…+n·2n,
2Tn=1·22+2·23+3·24+…+(n-1)·2n+n·2n+1,
两式作差得-Tn=2+22+23+…+2n-n·2n+1.
Tn=2+(n-1)·2n+1.
[再练一题]
3.已知正项数列{an}中,a1=1,点(,an+1)(n∈N+)在函数y=x2+1的图象上,数列{bn}的前n项和Sn=2-bn.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=,求{cn}的前n项和Tn.
【解】 (1)∵点(n∈N+)在函数y=x2+1的图象上,
∴an+1=an+1,∴数列{an}是公差为1的等差数列.
∵a1=1,∴an=1+(n-1)=n,
∵Sn=2-bn,∴Sn+1=2-bn+1,
两式相减得:bn+1=-bn+1+bn,即=,
由S1=2-b1,即b1=2-b1,得b1=1.
∴数列{bn}是首项为1,公比为的等比数列,
∴bn=.
(2)log2bn+1=log2=-n,
10
∴cn==-,
∴Tn=c1+c2+…+cn=+++…+=1-=.
函数思想求解数列问题
数列是一种特殊的函数,在求解数列问题时,若涉及参数取值范围,最值问题或单调性时,均可考虑采用函数的思想解题.值得注意的是数列定义域是正整数集或其真子集,这一特殊性对问题结果可能造成影响.
已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n=1,2,3,….
(1)求证:数列{lg(1+an)}是等比数列;
(2)设Tn=(1+a1)(1+a2)…(1+an),求Tn及数列{an}的通项公式;
(3)记bn=+,求数列{bn}的前n项和Sn,并说明Sn+=1.
【精彩点拨】 对于(1),由条件知an+1=a+2an,变形为an+1+1=(an+1)2,两边取对数即可得证.对于(3),由条件知an+1=a+2an=an(an+2),变形得=,即得=-,所以bn=2,由此Sn可求.
【规范解答】 (1)证明:由已知得an+1=a+2an,
∴an+1+1=(an+1)2.
∵a1=2,∴an+1>1,
两边取对数得lg(1+an+1)=2lg(1+an),
即=2.
∴数列{lg(1+an)}是公比为2的等比数列.
(2)由(1)知lg(1+an)=2n-1·lg(1+a1)=2n-1·lg 3
=lg 32n-1,
∴1+an=3. (*)
∴Tn=(1+a1)(1+a2)…(1+an)=3·3·3·…·3=3+2+2+…+2=3
由(*)式得an=3-1.
(3)∵an+1=a+2an,∴an+1=an(an+2),
10
∴=,∴=-.
又∵bn=+,∴bn=2,
∴Sn=b1+b2+…+bn
=2
=2.
∵an=32n-1-1,∴an+1=32n-1,
又∵a1=2,∴Sn=1-.
又∵Tn=32n-1,
∴Sn+=1-+=1.
[再练一题]
4.已知等差数列{an}的首项a1=1,公差d>0,且第二项、第五项、第十四项分别是一个等比数列的第二项、第三项、第四项.
【导学号:18082041】
(1)求数列{an}的通项公式;
(2)设bn=(n∈N+),Sn=b1+b2+…+bn,是否存在t,使得对任意的n均有Sn>总成立?若存在,求出最大的整数t;若不存在,请说明理由.
【解】 (1)由题意得(a1+d)(a1+13d)=(a1+4d)2,整理得2a1d=d2.∵d>0,
∴d=2.∵a1=1.∴an=2n-1(n∈N+).
(2)bn===,
∴Sn=b1+b2+…+bn=++…+-==.
假设存在整数t满足Sn>总成立,
又Sn+1-Sn=-
=>0,
∴数列{Sn}是单调递增的.∴S1=为Sn的最小值,故<,即t<9.
又∵t∈Z,
10
∴适合条件的t的最大值为8.
1.已知等差数列{an}前9项的和为27,a10=8,则a100=( )
A.100 B.99 C.98 D.97
【解析】 法一:∵{an}是等差数列,设其公差为d,
∴S9=(a1+a9)=9a5=27,∴a5=3.
又∵a10=8,∴∴
∴a100=a1+99d=-1+99×1=98.故选C.
法二:∵{an}是等差数列,
∴S9=(a1+a9)=9a5=27,∴a5=3.
在等差数列{an}中,a5,a10,a15,…,a100成等差数列,且公差d′=a10-a5=8-3=5.
故a100=a5+(20-1)×5=98.故选C.
【答案】 C
2.已知{an}是等差数列,Sn是其前n项和.若a1+a=-3,S5=10,则a9的值是________.
【解析】 法一:设等差数列{an}的公差为d,由S5=10,知S5=5a1+d=10,得a1+2d=2,即a1=2-2d.所以a2=a1+d=2-d,代入a1+a=-3,化简得d2-6d+9=0,所以d=3,a1=-4.故a9=a1+8d=-4+24=20.
法二:设等差数列{an}的公差为d,由S5=10,知=5a3=10,所以a3=2.
所以由a1+a3=2a2,得a1=2a2-2,代入a1+a=-3,化简得a+2a2+1=0,所以a2=-1.
公差d=a3-a2=2+1=3,故a9=a3+6d=2+18=20.
【答案】 20
3.已知各项都为正数的数列{an}满足a1=1,a-(2an+1-1)an-2an+1=0.
(1)求a2,a3;
(2)求{an}的通项公式.
【解】 (1)由题意可得a2=,a3=.
(2)由a-(2an+1-1)an-2an+1=0得
2an+1(an+1)=an(an+1).
10
因为{an}的各项都为正数,所以=.
故{an}是首项为1,公比为的等比数列,因此an=.
4.已知{an}是等比数列,前n项和为Sn(n∈N+),且-=,S6=63.
(1)求{an}的通项公式;
(2)若对任意的n∈N+,bn是log2an和log2an+1的等差中项,求数列{(-1)nb}的前2n项和.
【解】 (1)设数列{an}的公比为q.
由已知,有-=,
解得q=2或q=-1.
又由S6=a1·=63,知q≠-1,
所以a1·=63,得a1=1.
所以an=2n-1.
(2)由题意,得bn=(log2an+log2an+1)
=(log22n-1+log22n)=n-,
即{bn}是首项为,公差为1的等差数列.
设数列{(-1)nb}的前n项和为Tn,则
T2n=(-b+b)+(-b+b)+…+(-b+b)
=b1+b2+b3+b4+…+b2n-1+b2n==2n2.
5.设数列{an}的前n项和为Sn,已知S2=4,an+1=2Sn+1,n∈N+.
(1)求通项公式an;
(2)求数列{|an-n-2|}的前n项和.
【解】 (1)由题意,得
则
又当n≥2时,由an+1-an=(2Sn+1)-(2Sn-1+1)=2an,得an+1=3an,
所以,数列{an}的通项公式为an=3n-1,n∈N+.
(2)设bn=|3n-1-n-2|,n∈N+,则b1=2,b2=1.
当n≥3时,由于3n-1>n+2,故bn=3n-1-n-2,n≥3.
设数列{bn}的前n项和为Tn,则T1=2,T2=3,
10
当n≥3时,Tn=3+-=,
所以,Tn=
10