2014年高考试题——数学理（湖南卷）原卷版

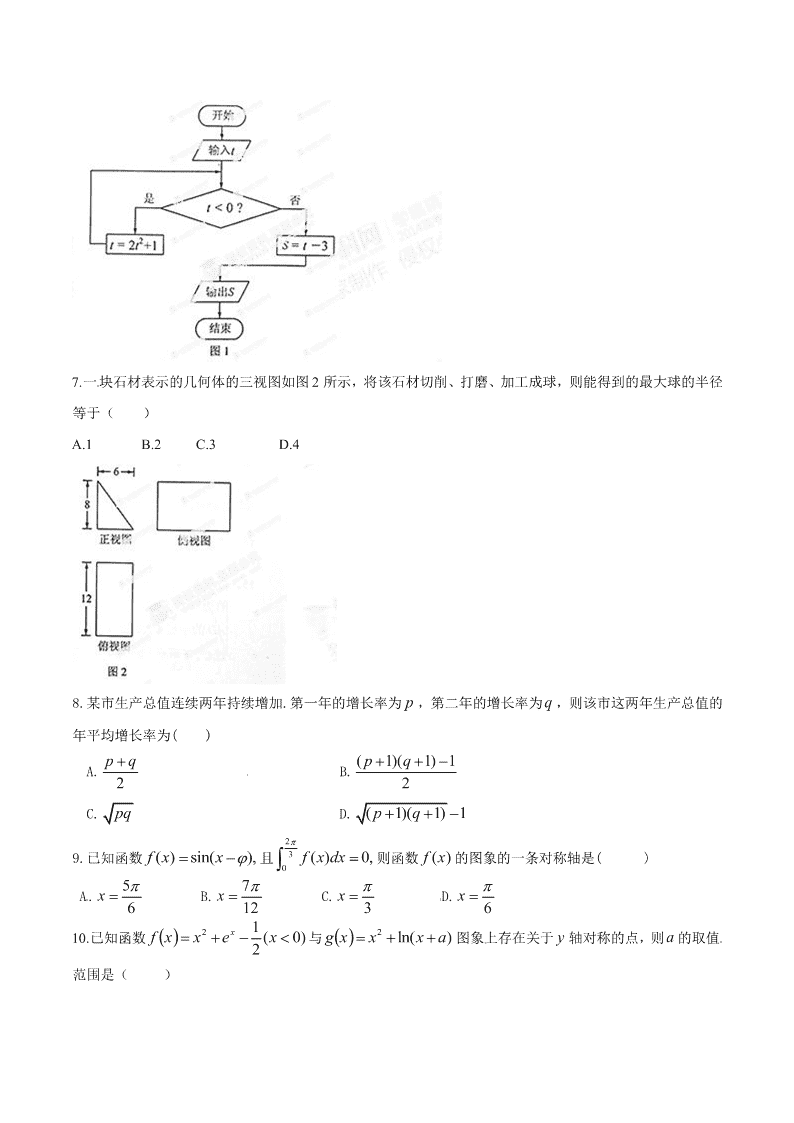
2014年高考试题——数学理（湖南卷）原卷版

一.选择题：本大题共 10 小题，每小题 5 分，共 50 分.在每小题给出的四个选项中，只有一项 是符合题目要求的. 1.满足 iz iz  （i 是虚数单位）的复数 z （ ） A. i2 1 2 1  B. i2 1 2 1  C. i2 1 2 1  D. i2 1 2 1  2.对一个容量为 N 的总体抽取容量为 n 的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法 抽取样本时，总体中每个个体被抽中的概率分别为 321 ,, ppp ，则（ ） A. 321 ppp  B. 132 ppp  C. 231 ppp  D. 321 ppp  3.已知 )(),( xgxf 分别是定义在 R 上的偶函数和奇函数，且 1)()( 23  xxxgxf ，则  )1()1( gf A. 3 B. 1 C. 1 D. 3 4. 51 22 xy 的展开式中 32 yx 的系数是（ ） A. 20 B. 5 C.5 D.20 5.已知命题 .,:,: 22 yxyxqyxyxp  则若；命题则若 在命题 ① qpqpqpqp  ）④（③② );(;; 中，真命题是（ ） A①③ B.①④ C.②③ D.②④ 6.执行如图 1 所示的程序框图，如果输入的 ]2,2[t ，则输出的 S 属于（ ） A. ]2,6[  B. ]1,5[  C. ]5,4[ D. ]6,3[ 7.一块石材表示的几何体的三视图如图 2 所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径 等于（ ） A.1 B.2 C.3 D.4 8.某市生产总值连续两年持续增加.第一年的增长率为 p ，第二年的增长率为 q ，则该市这两年生产总值的 年平均增长率为( ) A. 2 pq B. ( 1)( 1) 1 2 pq   [来源:学科网] C. pq D. ( 1)( 1) 1pq   9.已知函数 ( ) sin( ),f x x 且 2 3 0 ( ) 0,f x dx   则函数 ()fx的图象的一条对称轴是( ) A. 5 6x  B. 7 12x  C. 3x  D. 6x  [来源:Z+xx+k.Com] 10.已知函数   )0(2 12  xexxf x 与   )ln(2 axxxg  图象上存在关于 y 轴对称的点，则 a 的取值 范围是（ ） A. )1,( e  B. ),( e C. ),1( e e  D. )1,( e e 二.填空题：本大题共 6 小题，考生作答 5 小题，没小题 5 分，共 25 分. (一)选做题（请考生在第 11,12,13 三题中任选两题作答，如果全做，则按前两题记分） 11.在平面直角坐标系中，倾斜角为 4  的直线l 与曲线 2 cos 1 sin xC y      ： ，（  为参数）交 于 A 、 B 两点， 且 2AB  ，以坐标原点O 为极点， x 轴正半轴为极轴建立极坐标系，则直线 的极坐标方程是________. 12.如图3，已知 AB ，BC 是 O 的两条弦，AO BC ， 3AB  ， 22BC  ，则 的半径等于________. 13.若关于 x 的不等式 23ax 的 解集为 51 33xx   ，则 a ________. (二)必做题（14-16 题） 14.若变量 yx, 满足约束条件       ky yx xy 4 ，且 yxz  2 的最小值为 6 ，则 ____k 15.如图 4，正方形 ABCD 和正方形 DEFG 的边长分别为  ,a b a b ，原点O 为 AD 的中点，抛物线 )0(22  ppxy 经过 FC, 两点，则 _____a b . [来源:学.科.网 Z.X.X.K] 16.在平面直角坐标系中,O 为原点,   ),0,3(),3,0(,0,1 CBA  动点 D 满足 CD =1，则 OA OB OD 的最 大值是_________. 三、解答题：本大题共 6 小题，共 75 分.解答应写出文字说明，证明过程或演算过程. 17. 某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为 2 3 和 3 5 ,现安排甲组研发新产品 A ,乙组研 发新产品 B .设甲,乙两组的研发是相互独立的. (1)求至少有一种新产品研发成功的概率; (2)若新产品 A 研发成功,预计企业可获得120万元,若新产品 B 研发成功,预计企业可获得利润100万元,求该 企业可获得利润的分布列和数学期望. 18.如图 5,在平面四边形 ABCD中, 1, 2, 7AD CD AC   . (1)求 cos CAD 的值; (2)若 7cos 14BAD   , 21sin 6CBA ,求 BC 的长. 19.如图 6,四棱柱 1 1 1 1ABCD A B C D 的所有棱长都相等, 1 1 1 1 1,AC BD O AC B D O,四边形 11ACC A 和四边形 11BDD B 为矩形. (1)证明: 1OO 底面 ABCD; (2)若 060CBA,求二面角 11C OB D的余弦值. 20.已知数列 na 满足 111, n nna a a p   , *nN . (1)若 na 为递增数列,且 1 2 3,2 ,3a a a 成等差数列,求 P 的值; (2)若 1 2p  ,且 21na  是递增数列, 2na 是递减数列,求数列 na 的通项公式. 21.如图 7, O 为坐标原点,椭圆 1 :C   22 2210xy abab    的左右焦点分别为 12,FF,离心率为 1e ;双曲线 2 :C 22 221xy ab的左右焦点分别为 34,FF,离心率为 2e ,已知 12 3 2ee  ,且 24 31FF . (1)求 12,CC的方程; (2)过 1F 点作 1C 的不垂直于 y 轴的弦 AB , M 为 AB 的中点,当直线 OM 与 2C 交于 ,PQ两点时,求四边形 APBQ 面积的最小值. [来源:学科网 ZXXK] 22.已知常数 0a  ,函数     2ln 1 2 xf x ax x    . (1)讨论  fx在区间 0, 上的单调性; (2)若  fx存在两个极值点 12,xx,且    120f x f x,求 a 的取值范围.[来源:学*科*网 Z*X*X*K]