【数学】2020届一轮复习人教版（理）第7章第7讲立体几何中的向量方法学案

【数学】2020届一轮复习人教版（理）第7章第7讲立体几何中的向量方法学案

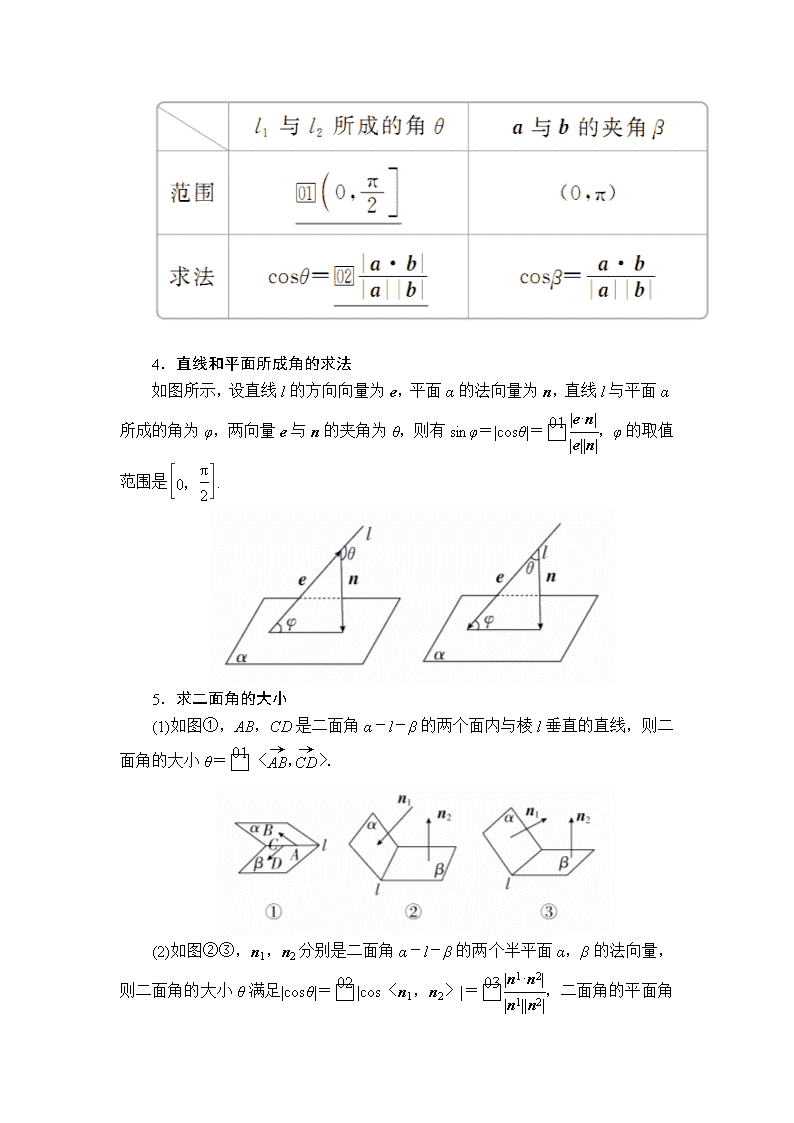
第7讲　立体几何中的向量方法 ‎[考纲解读]　1.理解直线的方向向量及平面的法向量，并能用向量语言表述线线、线面、面面的平行和垂直关系．(重点)‎ ‎2.能用向量方法证明立体几何中有关线面位置关系的一些简单定理，并能用向量方法解决线线、线面、面面的夹角的计算问题．(难点)‎ ‎[考向预测]　从近三年高考情况来看，本讲为高考必考内容．预测2020年高考将会以空间向量为工具，证明平行与垂直以及求空间角的计算问题．试题以解答题的形式呈现，难度为中等偏上.‎ ‎1．用向量证明空间中的平行关系 ‎(1)设直线l1和l2的方向向量分别为v1和v2，则l1∥l2(或l1与l2重合)⇔v1∥v2⇔v1＝λv2.‎ ‎(2)设直线l的方向向量为v，与平面α共面的两个不共线向量v1和v2，则l∥α或l⊂α⇔存在两个实数x，y，使v＝xv1＋yv2.‎ ‎(3)设直线l的方向向量为v，平面α的法向量为u，则l∥α或l⊂α⇔v⊥u⇔v·u＝0.‎ ‎(4)设平面α和β的法向量分别为u1，u2，则α∥β⇔u1∥u2⇔u1＝λu2.‎ ‎2．用向量证明空间中的垂直关系 ‎(1)设直线l1和l2的方向向量分别为v1和v2，则l1⊥l2⇔v1⊥v2⇔v1·v2＝0.‎ ‎(2)设直线l的方向向量为v，平面α的法向量为u，则l⊥α⇔v∥u⇔v＝λu.‎ ‎(3)设平面α和β的法向量分别为u1和u2，则α⊥β⇔u1⊥u2⇔u1·u2＝0.‎ ‎3．两条异面直线所成角的求法 设a，b分别是两异面直线l1，l2的方向向量，则 ‎4．直线和平面所成角的求法 如图所示，设直线l的方向向量为e，平面α的法向量为n，直线l与平面α所成的角为φ，两向量e与n的夹角为θ，则有sinφ＝|cosθ|＝，φ的取值范围是.‎ ‎5．求二面角的大小 ‎(1)如图①，AB，CD是二面角α－l－β的两个面内与棱l垂直的直线，则二面角的大小θ＝〈，〉．‎ ‎(2)如图②③，n1，n2分别是二面角α－l－β的两个半平面α，β的法向量，则二面角的大小θ满足|cosθ|＝|cos〈n1，n2〉|＝，二面角的平面角大小是向量n1与n2的夹角(或其补角)‎ ‎1．概念辨析 ‎(1)若空间向量a平行于平面α，则a所在直线与平面α平行．(　　)‎ ‎(2)两异面直线夹角的范围是，直线与平面所成角的范围是，二面角的范围是[0，π]．(　　)‎ ‎(3)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角．(　　)‎ ‎(4)若二面角α－a－β的两个半平面α，β的法向量n1，n2所成角为θ，则二面角α－a－β的大小是π－θ.(　　)‎ 答案　(1)×　(2)√　(3)×　(4)×‎ ‎2．小题热身 ‎(1)若直线l的方向向量为a＝(1,0,2)，平面α的法向量为n＝(－2,0，－4)，则(　　)‎ A．l∥α B．l⊥α C．l⊂α D．l与α斜交 答案　B 解析　因为a＝(1,0,2)，n＝(－2,0，－4)，‎ 所以n＝－2a，所以a∥n，所以l⊥α.‎ ‎(2)已知向量＝(2,2,1)，＝(4,5,3)，则平面ABC的单位法向量是(　　)‎ A. B． C．± D．± 答案　D 解析　设平面ABC的一个法向量是n＝(x，y，z)，则取z＝1，得x＝，y＝－1.则n＝，|n|＝，故平面ABC的单位法向量是±.‎ ‎(3)在正三棱柱ABC－A1B1C1中，若AB＝BB1，则AB1与C1B所成角的大小为(　　)‎ A．60° B．75°‎ C．90° D．105°‎ 答案　C 解析　取AC的中点D，建立如图所示的空间直角坐标系．‎ 设AB＝a，则B，C1，A，B1，从而＝，＝.‎ 所以cos〈，〉＝＝0，‎ 所以AB1与C1B所成的角为90°.故选C.‎ ‎(4)在长方体ABCD－A1B1C1D1中，AB＝2，BC＝AA1＝1，则D1C1与平面A1BC1所成角的正弦值为________，二面角B－A1C1－D1的余弦值为________．‎ 答案　　－ 解析　如图，建立空间直角坐标系Dxyz，则 D1(0,0,1)，C1(0,2,1)，A1(1,0,1)，B(1,2,0)，‎ ‎∴＝(0,2,0)，＝(－1，2,0)，‎ ＝(0,2，－1)，‎ 设平面A1BC1的一个法向量为n＝(x，y，z)，‎ 由即 令y＝1，得n＝(2,1,2)，‎ 设D1C1与平面A1BC1所成角为θ，则 sinθ＝|cos〈，n〉|＝＝＝，‎ 即直线D1C1与平面A1BC1所成角的正弦值为.‎ 易知平面A1C1D1的法向量m＝(0,0,1)，‎ ‎∴cos〈m，n〉＝＝＝.‎ 由图可知，二面角B－A1C1－D1为钝角，‎ 故二面角B－A1C1－D1的余弦值为－.‎ 题型 　利用空间向量研究空间中的位置关系 角度1　利用空间向量证明平行与垂直问题 ‎1．(2018·青岛模拟)如图，在多面体ABC－A1B1C1中，四边形A1ABB1是正方形，AB＝AC，BC＝AB，B1C1綊BC，AA1⊥平面BAC.‎ 求证：(1)A1B1⊥平面AA1C；‎ ‎(2)AB1∥平面A1C1C.‎ 证明　∵AA1⊥平面BAC.‎ ‎∴AA1⊥AB，AA1⊥AC.‎ 又∵AB＝AC，BC＝AB，‎ ‎∴∠CAB＝90°，即CA⊥AB，‎ ‎∴AB，AC，AA1两两互相垂直．‎ 建立如图所示的空间直角坐标系Axyz，设AB＝2，则 A(0,0,0)，B1(0,2,2)，A1(0,0,2)，‎ C(2,0,0)，‎ C1(1,1,2)．‎ ‎(1)＝(0,2,0)，＝(0,0，－2)，＝(2,0,0)，设平面AA1C的一个法向量n＝(x，y，z)，‎ 则即即 取y＝1，则n＝(0,1,0)．‎ ‎∴＝2n，即∥n.‎ ‎∴A1B1⊥平面AA1C.‎ ‎(2)易知＝(0,2,2)，＝(1,1,0)，＝(2,0，－2)，设平面A1C1C的一个法向量m＝(x1，y1，z1)，‎ 则即 令x1＝1，则y1＝－1，z1＝1，即m＝(1，－1,1)．‎ ‎∴·m＝0×1＋2×(－1)＋2×1＝0，‎ ‎∴⊥m.又AB1⊄平面A1C1C，‎ ‎∴AB1∥平面A1C1C.‎ 角度2　利用空间向量解决平行与垂直关系中的探索性问题 ‎2．(2018·桂林模拟)如图，棱柱ABCD－A1B1C1D1的所有棱长都等于2，∠ABC和∠A1AC均为60°，平面AA1C1C⊥平面ABCD.‎ ‎(1)求证：BD⊥AA1；‎ ‎(2)在直线CC1上是否存在点P，使BP∥平面DA1C1，若存在，求出点P的位置，若不存在，请说明理由．‎ 解　(1)证明：设BD与AC交于点O，则BD⊥AC，连接A1O，在△AA1O中，AA1＝2，AO＝1，∠A1AO＝60°，‎ ‎∴A1O2＝AA＋AO2－2AA1·AOcos60°＝3，‎ ‎∴AO2＋A1O2＝AA，‎ ‎∴A1O⊥AO.‎ 由于平面AA1C1C⊥平面ABCD，且平面AA1C1C∩平面ABCD＝AC，A1O⊂平面AA1C1C，‎ ‎∴A1O⊥平面ABCD.‎ 以OB，OC，OA1所在直线分别为x轴、y轴、z轴，建立如图所示的空间直角坐标系，则 A(0，－1,0)，B(，0,0)，‎ C(0,1,0)，D(－，0,0)，‎ A1(0,0，)，C1(0,2，)．‎ 由于＝(－2，0,0)，＝(0,1，)，‎ ·＝0×(－2)＋1×0＋×0＝0，‎ ‎∴⊥，即BD⊥AA1.‎ ‎(2)假设在直线CC1上存在点P，使BP∥平面DA1C1，‎ 设＝λ，P(x，y，z)，则(x，y－1，z)＝λ(0,1，)．‎ 从而有P(0,1＋λ，λ)，＝(－，1＋λ，λ)．设平面DA1C1的法向量为n＝(x，y，z)，则 又＝(0,2,0)，＝(，0，)，‎ 则取n＝(1,0，－1)，‎ 因为BP∥平面DA1C1，‎ 则n⊥，即n·＝－－λ＝0，‎ 得λ＝－1，‎ 即点P在C1C的延长线上，且C1C＝CP.‎ ‎1．用空间向量证明平行问题的方法 线线平行 证明两直线的方向向量共线 线面平行 ‎①证明该直线的方向向量与平面的某一法向量垂直；‎ ‎②证明直线的方向向量与平面内某直线的方向向量平行；‎ ‎③证明该直线的方向向量可以用平面内的两个不共线的向量线性表示 面面平行 ‎①证明两平面的法向量平行(即为共线向量)；‎ ‎②转化为线面平行、线线平行问题 ‎2．用空间向量证明垂直问题的方法 线线垂 直问题 证明两直线所在的方向向量互相垂直，即证它们的数量积为零 线面垂 直问题 直线的方向向量与平面的法向量共线，或利用线面垂直的判定定理转化为证明线线垂直 面面垂 直问题 两个平面的法向量垂直，或利用面面垂直的判定定理转化为证明线面垂直 ‎3．解决立体几何中探索性问题的基本方法 ‎(1)通常假设题中的数学对象存在(或结论成立)，然后在这个前提下进行逻辑推理．‎ ‎(2)探索性问题的关键是设点：①空间中的点可设为(x，y，z)；②坐标平面内的点其中一个坐标为0，如xOy面上的点为(x，y,0)；③坐标轴上的点两个坐标为0，如z轴上的点为(0,0，z)；④直线(线段)AB上的点P，可设为＝λ，表示出点P的坐标，或直接利用向量运算．‎ 提醒：解这类问题时要利用好向量垂直和平行的坐标表示．　 　　　　　　　　　　　　　　　　　　‎ ‎1．如图，在四棱锥P－ABCD中，底面ABCD是边长为a的正方形，侧面PAD⊥底面ABCD，且PA＝PD＝AD，设E，F分别为PC，BD的中点．‎ ‎(1)求证：EF∥平面PAD；‎ ‎(2)求证：平面PAB⊥平面PDC.‎ 证明　(1)如图，取AD的中点O，连接OP，OF.‎ 因为PA＝PD，所以PO⊥AD.‎ 因为侧面PAD⊥底面ABCD，平面PAD∩平面ABCD＝AD，PO⊂平面PAD，‎ 所以PO⊥平面ABCD.‎ 又O，F分别为AD，BD的中点，‎ 所以OF∥AB.‎ 又ABCD是正方形，所以OF⊥AD.‎ 因为PA＝PD＝AD，‎ 所以PA⊥PD，OP＝OA＝.‎ 以O为原点，OA，OF，OP所在直线分别为x轴、y轴、z轴建立空间直角坐标系，‎ 则A，F，D，‎ P，B，C.‎ 因为E为PC的中点，所以E.‎ 易知平面PAD的一个法向量为＝，‎ 因为＝，‎ 且·＝·＝0，‎ 又因为EF⊄平面PAD，‎ 所以EF∥平面PAD.‎ ‎(2)因为＝，＝(0，－a,0)，‎ 所以·＝·(0，－a,0)＝0，‎ 所以⊥，所以PA⊥CD.‎ 又PA⊥PD，PD∩CD＝D，‎ PD，CD⊂平面PDC，‎ 所以PA⊥平面PDC.‎ 又PA⊂平面PAB，‎ 所以平面PAB⊥平面PDC.‎ ‎2．如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图，在直观图中，点M是BD的中点，AE＝CD，侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示．‎ ‎(1)求证：EM∥平面ABC；‎ ‎(2)试问在棱CD上是否存在一点N，使MN⊥平面BDE？若存在，确定点N的位置；若不存在，请说明理由．‎ 解　以A为原点，建立如图所示的空间直角坐标系，则 A(0,0,0)，B(0,2,0)，C(－2,0,0)，D(－2,0,4)，‎ E(0,0,2)，M(－1,1,2)，＝(0,0,2)，‎ ＝(2,2，－4)，＝(2,0，－2)，‎ ＝(0,0，－4)，＝(1,1，－2)，＝(－1,1,0)．‎ ‎(1)证明：由图易知为平面ABC的一个法向量，‎ 因为·＝0×(－1)＋0×1＋2×0＝0，‎ 所以⊥，即AE⊥EM，‎ 又EM⊄平面ABC，‎ 故EM∥平面ABC.‎ ‎(2)假设在DC上存在一点N满足题意，‎ 设＝λ＝(0,0，－4λ)，λ∈[0,1]，‎ 则＝－＝(1,1，－2)－(0,0，－4λ)＝(1,1，－2＋4λ)，所以即 解得λ＝∈[0,1]．‎ 所以棱DC上存在一点N，满足NM⊥平面BDE，此时DN＝DC.‎ 题型 　利用空间向量求解空间角 角度1　利用空间向量求解异面直线所成的角 ‎1．(2015·全国卷Ⅰ)如图，四边形ABCD为菱形，∠ABC＝120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE＝2DF，AE⊥EC.‎ ‎(1)证明：平面AEC⊥平面AFC；‎ ‎(2)求直线AE与直线CF所成角的余弦值．‎ 解　(1)证明：连接BD.‎ 设BD∩AC＝G，连接EG，FG，EF.‎ 在菱形ABCD中，不妨设GB＝1.‎ 由∠ABC＝120°，可得AG＝GC＝.‎ 由BE⊥平面ABCD，AB＝BC，可知AE＝EC.‎ 又AE⊥EC，所以EG＝，且EG⊥AC.‎ 在Rt△EBG中，可得BE＝，故DF＝.‎ 在Rt△FDG中，可得FG＝.‎ 在直角梯形BDFE中，由BD＝2，BE＝，DF＝，可得EF＝.‎ 从而EG2＋FG2＝EF2，所以EG⊥FG.‎ 又AC∩FG＝G，可得EG⊥平面AFC.‎ 因为EG⊂平面AEC，所以平面AEC⊥平面AFC.‎ ‎(2)如图，以G为坐标原点，分别以，的方向为x轴，y轴正方向，||为单位长度，建立空间直角坐标系Gxyz.‎ 由(1)可得A(0，－，0)，E(1,0，)，F，C(0，，0)，‎ 所以＝(1，，)，＝.‎ 故cos〈，〉＝＝－.‎ 所以直线AE与直线CF所成角的余弦值为.‎ 角度2　利用空间向量求解直线与平面所成的角(多维探究)‎ ‎2．(2018·全国卷Ⅱ)如图，在三棱锥P－ABC中，AB＝BC＝2，PA＝PB＝PC＝AC＝4，O为AC的中点．‎ ‎(1)证明：PO⊥平面ABC；‎ ‎(2)若点M在棱BC上，且二面角M－PA－C为30°，求PC与平面PAM所成角的正弦值．‎ 解　(1)证明：因为AP＝CP＝AC＝4，O为AC的中点，所以OP⊥AC，且OP＝2.‎ 连接OB.因为AB＝BC＝AC，所以△ABC为等腰直角三角形，且OB⊥AC，OB＝AC＝2.‎ 由OP2＋OB2＝PB2，知OP⊥OB.‎ 由OP⊥OB，OP⊥AC，AC∩OB＝O，知PO⊥平面ABC.‎ ‎(2)如图，以O为坐标原点，的方向为x轴正方向，建立如图所示的空间直角坐标系Oxyz.‎ 由已知得O(0,0,0)，‎ B(2,0,0)，A(0，－2,0)，‎ C(0,2,0)，P(0,0,2)，‎ 则＝(0,2，2)，‎ 取平面PAC的法向量＝(2,0,0)．‎ 设M(a,2－a,0)(00)，则 A1(0，－4，λ)，B(3,0,0)，‎ C1(0,4，λ)，D(0,0,0)，‎ ‎∴＝(0，－4，λ)，＝(0,4，λ)，＝(3,0,0)，‎ 设平面BC1D的法向量为n＝(x，y，z)，‎ 则即则x＝0，令z＝4，可得y＝－λ，‎ 故n＝(0，－λ，4)为平面BC1D的一个法向量．‎ 设直线A1D与平面BC1D所成角为θ，‎ 则sinθ＝|cos〈n，〉|＝ ‎＝＝，‎ 解得λ＝2或λ＝8，即AA1＝2或AA1＝8.‎ ‎3．(2018·芜湖模拟)如图，在三棱柱ABC－A1B1C1中，∠AA1B1＝45°，AC＝BC，平面BB1C1C⊥平面AA1B1B，E为CC1的中点．‎ ‎(1)求证：BB1⊥AC；‎ ‎(2)若AA1＝2，AB＝，直线A1C1与平面ABB1A1所成角为45°，求平面A1B1E与平面ABC所成锐二面角的余弦值．‎ 解　(1)证明：过点C作CO⊥BB1交BB1于O，因为平面BB1C1C⊥平面AA1B1B，BB1C1C∩平面AA1B1B＝B1B，所以CO⊥平面AA1B1B，故CO⊥OA，‎ 又因为AC＝BC，OC＝OC，所以Rt△AOC≌Rt△BOC，故OA＝OB，‎ 因为∠AA1B1＝∠OBA＝45°，所以AO⊥BB1，又因为BB1⊥CO，所以BB1⊥平面AOC，故BB1⊥AC.‎ ‎(2)以O为坐标原点，OA，OB，OC所在直线为x，y，z轴，建立空间直角坐标系Oxyz，‎ ‎∵AC∥A1C1，直线A1C1与平面ABB1A1所成角为45°，∴直线AC与平面ABB1A1所成角为45°，∵CO⊥平面AA1B1B，∴∠CAO＝45°，则A(1,0,0)，B(0,1,0)，C(0,0,1)，A1(1，－2,0)，B1(0，－1，0)，E(0，－1,1)，‎ 设平面A1B1E的法向量为n＝(x1，y1，z1)，‎ 则∴ 令x1＝1，得n＝(1,1,0)；‎ 设平面ABC的法向量为m＝(x2，y2，z2)，则 ∴ 令x2＝1，得m＝(1,1,1)；‎ ‎∴cos〈m，n〉＝＝，平面A1B1E与平面ABC所成锐二面角的余弦值为.‎ 题型 　求空间距离(供选用)‎ ‎(2018·合肥三模)如图，在多面体ABCDE中，平面ABD⊥平面ABC，AB⊥AC，AE⊥BD，DE綊AC，AD＝BD＝1.‎ ‎(1)求AB的长；‎ ‎(2)已知2≤AC≤4，求点E到平面BCD的距离的最大值．‎ 解　(1)∵平面ABD⊥平面ABC，且交线为AB，而AC⊥AB，∴AC⊥平面ABD.‎ 又∵DE∥AC，∴DE⊥平面ABD，从而DE⊥BD.‎ 注意到BD⊥AE，且DE∩AE＝E，∴BD⊥平面ADE，‎ 于是，BD⊥AD.而AD＝BD＝1，∴AB＝.‎ ‎(2)∵AD＝BD，取AB的中点为O，∴DO⊥AB.‎ 又∵平面ABD⊥平面ABC，∴DO⊥平面ABC.‎ 过O作直线OY∥AC，以点O为坐标原点，直线OB，OY，OD分别为x，y，z轴，建立空间直角坐标系Oxyz，如图所示．‎ 记AC＝2a，则1≤a≤2，‎ A，B，‎ C，D，E，‎ ＝(－，2a,0)，＝.‎ 设平面BCD的法向量为n＝(x，y，z)．‎ 由得 令x＝，得n＝.‎ 又∵＝(0，－a,0)，‎ ‎∴点E到平面BCD的距离d＝＝ .‎ ‎∵1≤a≤2，∴当a＝2时，d取得最大值，‎ dmax＝＝.‎ 空间距离的几个结论 ‎(1)点到直线的距离：设过点P的直线l的方向向量为单位向量n，A为直线l外一点，点A到直线l的距离d＝.‎ ‎(2)点到平面的距离：设P为平面α内的一点，n为平面α的法向量，A为平面α外一点，点A到平面α的距离d＝.‎ ‎(3)线面距离、面面距离都可以转化为点到面的距离．　 　　　　　　　　　　　　　　　　　　‎ ‎(2018·惠州第一次调研)如图，已知圆柱OO1底面半径为1，高为π，平面ABCD是圆柱的一个轴截面，动点M从点B出发沿着圆柱的侧面到达点D，其运动路程最短时在侧面留下曲线Γ.将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后得到平面A1B1C1D1，边B1C1与曲线Γ相交于点P.‎ ‎(1)求曲线Γ的长度；‎ ‎(2)当θ＝时，求点C1到平面APB的距离．‎ 解　(1)将圆柱一半展开后底面的半个圆周变成长方形的边BA，曲线Γ就是对角线BD.‎ 由于AB＝πr＝π，AD＝π，∴BD＝π.‎ 故曲线Γ的长度为π.‎ ‎(2)当θ＝时，建立如图所示的空间直角坐标系，‎ 则O(0,0,0)，A(0，－1,0)，B(0,1,0)，‎ P，C1(－1，0，π)，则＝(0,2,0)，＝，＝(－1,0，π)，‎ 设平面ABP的法向量为n＝(x，y，z)，‎ 则 取z＝2得n＝(π，0,2)，‎ ‎∴点C1到平面PAB的距离d＝＝ .‎ 易错防范　向量法求空间角 ‎[典例]　如图，在多面体ADEFCB中，ABFE是直角梯形，∠AEF＝90°，AE∥BF，DCFE为正方形，且AE＝1，BF＝EF＝2，∠BFC＝60°.‎ ‎(1)求证：CE∥平面ADB；‎ ‎(2)求直线AB与平面EFCD所成角的正弦值．‎ 解　(1)证明：如图，取FB的中点M，连接CM，EM，AM.‎ ‎∵AE∥BM，AE＝BM，‎ ‎∴四边形AEMB为平行四边形，‎ ‎∴AB∥EM，‎ 同理AM∥EF，AM＝EF，‎ ‎∴AM∥EF∥CD，AM＝EF＝CD，‎ ‎∴四边形AMCD为平行四边形，‎ ‎∴AD∥CM，‎ 又CM∩EM＝M，AB∩AD＝A，‎ ‎∴平面CME∥平面ADB，‎ 又CE⊂平面CME，∴CE∥平面ADB.‎ ‎(2)由(1)可知AB∥EM，‎ ‎∴直线AB与平面EFCD所成的角就是直线EM与平面EFCD所成的角．‎ 过M作MN⊥CF于点N，连接EN，‎ 由于ABFE是直角梯形，∠AEF＝90°，AE∥BF，EFCD为正方形，‎ ‎∴∠EFB＝90°，∠EFC＝90°，‎ ‎∴EF⊥平面BFC，∴EF⊥MN，‎ ‎∴MN⊥平面EFCD.‎ 以N为坐标原点，的方向为x轴正方向，的方向为y轴正方向，的方向为z轴正方向建立如图所示的空间直角坐标系，‎ ‎∵M为FB的中点，∴MF＝1.‎ ‎∵∠BFC＝60°，∴MN＝，NF＝.‎ ‎∴N(0,0,0)，M，E，‎ ＝.‎ 易知平面EFCD的一个法向量为n＝(0,0,1)，‎ 设直线AB与平面EFCD所成角的大小为α，则sinα＝|cos〈n，〉|＝＝，‎ ‎∴直线AB与平面EFCD所成角的正弦值为.‎ 防范措施　向量法求空间角要注意的问题 (1)建立空间直角坐标系时 ‎①证明线面垂直关系，为建系作准备，没有文字说明，直接建系通常会扣分.‎ ‎②合理选择建系方法，从而有利于求向量的坐标.‎ (2)准确计算 利用空间向量法解决立体几何问题，计算一定要准确，避免因一个点的坐标错误导致整个题目全错的情况.‎