数学（理）卷·2018届陕西省汉中市高三下学期第二次教学质量检测（2018

数学（理）卷·2018届陕西省汉中市高三下学期第二次教学质量检测（2018

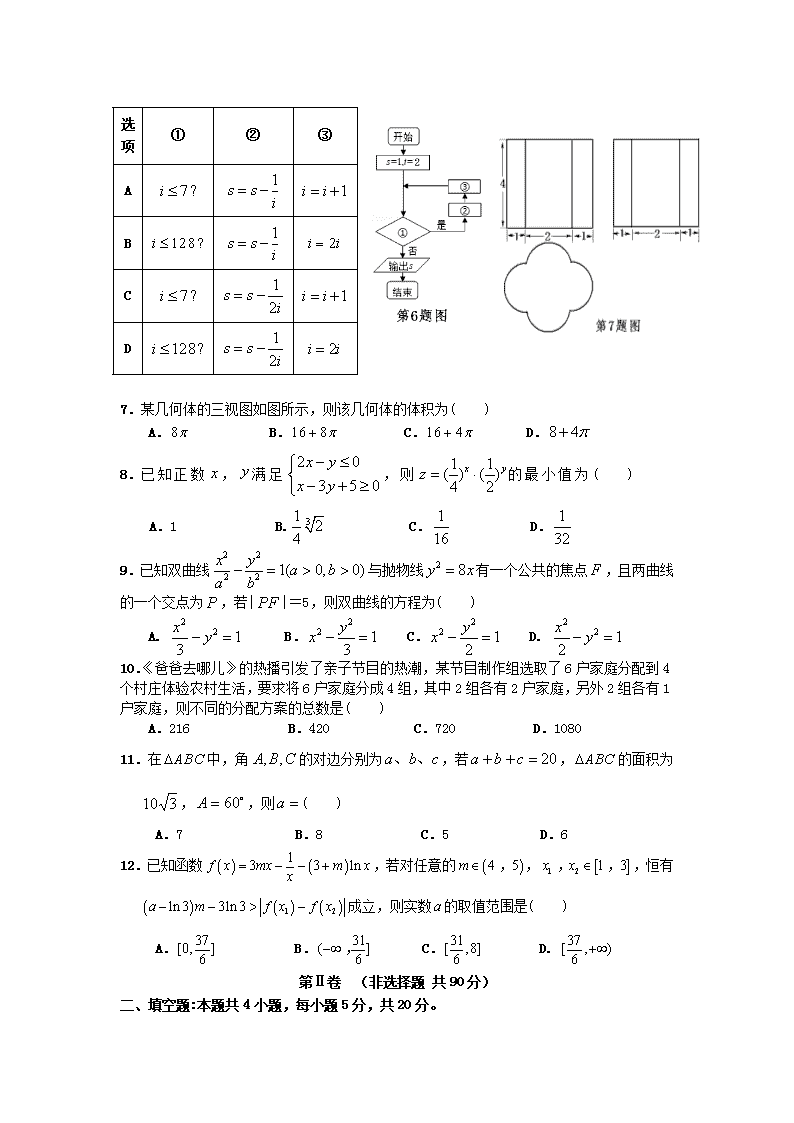
汉中市2018届高三年级教学质量第二次检测考试 理科数学 本试卷共23题，共150分，共4页。考试结束后，将本试卷和答题卡一并交回。‎ 注意事项：1.答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。‎ ‎2.选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。‎ ‎3.请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。‎ ‎4.作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。‎ ‎5.保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。‎ ‎ 第I卷 （选择题 共60分）‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．设集合，则(　　)‎ ‎ A. B. C. D.‎ ‎2．已知为虚数单位，复数满足，则为(　　)‎ A. B. 1 C. D.‎ ‎3．总体由编号为01，02，,19，20的20个个体组成。如图,利用图中的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取,每次选取两个数字，则选出来的第5个个体的编号为(　　) ‎ ‎ A.08 B.07 C.02 D.01‎ ‎4．要得到函数的图像，可以将函数的图像(　　) A.向左平移个周期 B.向右平移个周期 ‎ C.向左平移个周期 D.向右平移个周期 ‎5．已知向量，则“”是“与夹角为锐角”的(　　)‎ A. 必要不充分条件 B. 充分不必要条件 C. 充要条件 D. 既不充分也不必要条件 ‎6．我国古代名著《庄子·天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每天截取一半，永远都截不完，现将该木棍依此规律截取。如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度（单位：尺），则①②③处可分别填入的是(　　)‎ 选项 ‎①‎ ‎②‎ ‎③‎ A B C D ‎7．某几何体的三视图如图所示，则该几何体的体积为(　　)‎ ‎ A． B． C． D． ‎ ‎8．已知正数，满足，则的最小值为(　　)‎ ‎ A．1 B. C． D．‎ ‎9．已知双曲线与抛物线有一个公共的焦点，且两曲线的一个交点为，若||＝5，则双曲线的方程为(　　)‎ A. 　　　B． C． D. ‎ ‎10．《爸爸去哪儿》的热播引发了亲子节目的热潮，某节目制作组选取了6户家庭分配到4个村庄体验农村生活，要求将6户家庭分成4组，其中2组各有2户家庭，另外2组各有1户家庭，则不同的分配方案的总数是(　　) ‎ ‎ A．216 B．420 C．720 D．1080‎ ‎11．在中，角的对边分别为，若，的面积为，，则(　　) ‎ ‎ A．7 B．8 C．5 D．6 ‎ ‎12．已知函数，若对任意的，，恒有成立，则实数的取值范围是(　　)‎ ‎ A． B． C． D. ‎ 第Ⅱ卷 （非选择题 共90分）‎ 二、填空题:本题共4小题，每小题5分，共20分。‎ ‎13．展开式中项的系数为 (用数字作答).‎ ‎14．已知正项等比数列中，，其前项和为，且，则 ．‎ ‎15.已知,圆关于直线对称，则的最小值为 .‎ ‎16.点为正方体的内切球球面上的动点，点为上一点，，若球的体积为，则动点的轨迹的长度为 ． ‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第1721题为必考题，每 ‎ ‎ 个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎（一）必考题：共60分。‎ ‎17.（本小题满分12分）‎ 已知二次函数的对称轴为直线，数列{}的前项和,.‎ ‎（1）求数列{}的通项公式；‎ ‎（2）设，求{}的前项和.‎ ‎18．（本小题满分12分）‎ 西成高铁的开通极大地方便了汉中人民的出行。开通之前必须检测轨道中某新技术的三项不同的指标Ⅰ、Ⅱ、Ⅲ是否合格。假设该新技术的指标Ⅰ、Ⅱ、Ⅲ独立检测合格的概率分别为、、，指标Ⅰ、Ⅱ、Ⅲ检测合格分别记4分、2分、4分，若某项指标不合格，则该项指标记0分，各项指标检测结果互不影响。‎ ‎（1）求该新技术检测得8分的概率；‎ ‎（2）记该新技术的三项指标中被检测合格的个数为随机变量ξ，求ξ的分布列与数学期望。‎ ‎19.（本小题满分12分）‎ ‎ 如图，在四棱锥中，平面⊥平面，⊥，‎ ‎＝，⊥，＝1，＝2，＝＝.‎ ‎（1）求证：⊥平面；‎ ‎（2）求直线与平面所成角的正弦值.‎ ‎20．（本小题满分12分）‎ 如图,椭圆的离心率是，长轴是圆的直径。点是椭圆的下顶点，，是过点且互相垂直的两条直线，与圆相交于，两点，交椭圆于另一点.‎ ‎（1）求椭圆的方程；（2）当的面积取最大值时，求直线的方程.‎ ‎21．（本小题满分12分）‎ 已知函数在[1，＋∞）上为增函数，且，，．‎ ‎（1）求的值；（2）若在[1，＋∞）上为单调函数，求的取值范围；‎ ‎（3）设，若在区间上至少存在一个，使得成立，‎ 求的取值范围．‎ ‎（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎22．[选修4—4：坐标系与参数方程]（本小题满分10分）‎ 在直角坐标系中，曲线的参数方程为 (其中为参数)，‎ 曲线的方程为，以坐标原点为极点，轴的正半轴为极轴建立极坐标系.‎ ‎（1）求曲线的普通方程和曲线的极坐标方程；‎ ‎（2）若射线与曲线,分别交于两点，求.‎ ‎23．[选修4—5：不等式选讲]（本小题满分10分）‎ 已知函数．‎ ‎（1）若不等式恒成立，求实数的最大值；‎ ‎（2）在（1）的条件下，若正数，，满足，求证：．‎ 汉中市2018届高三年级教学质量第二次检测考试 理科数学参考答案 一、 选择题：‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B A D C A B B C B D A D 二、填空题： 13.112 14.15 15. 16. ‎ 三、解答题 ‎17. 解:(1)依题意，a＝4.--------------2分 ‎∴Sn＝n2－4n. -----------------------------4分 当n＝1时，a1＝S1＝1－4＋4＝-3；当n≥2时，an＝Sn－Sn－1＝2n－5.‎ 将a1 带入成立, 所以an＝2n－5 -----------------------------6分 ‎(2)由题知 cn＝ ‎ ‎--------------------------12分 ‎18. 解:(1)记“该新技术的三项指标Ⅰ、Ⅱ、Ⅲ独立检测合格”分别为事件A，B，C，则P(A)＝，P(B)＝，P(C)＝，所以事件“该新技术检测得分为8分”可表示为AC.‎ 所以该新技术量化检测得分为8分的概率为 P(AC)＝P(A)P()P(C)＝××＝.-----------------------------4分 ‎(2)ξ的所有可能取值为0，1，2，3.‎ 由题意结合(1)知，P(ξ＝0)＝P()＝××＝，---------5分 P(ξ＝1)＝P(A＋B＋C)＝××＋××＋××＝.‎ P(ξ＝2)＝P(AB＋AC＋BC)＝××＋××＋××＝.‎ P(ξ＝3)＝P(ABC)＝××＝. ------8分 所以随机变量ξ的分布列为 ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 所以E(ξ)＝0×＋1×＋2×＋3×＝.---------12分 ‎19. (1)证明:　因为平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，AB⊥AD，‎ 所以AB⊥平面PAD，所以AB⊥PD. --------------2分 又PA⊥PD，AB∩PA＝A，所以PD⊥平面PAB. --------------4分 ‎(2)解:　取AD的中点O，连接PO，CO. --------------6分 因为PA＝PD，所以PO⊥AD,PO平面PAD，平面PAD⊥平面ABCD，‎ 所以PO⊥平面ABCD.因为CO平面ABCD，所以PO⊥CO.‎ 因为AC＝CD，所以CO⊥AD. --------------8分 如图，建立空间直角坐标系O－xyz.由题意得，‎ A(0，1，0)，B(1，1，0)，C(2，0，0)，D(0，－1，0)，P(0，0，1).‎ 设平面PCD的一个法向量为n＝(x，y，z)，则 即--------------10分 令z＝2，则x＝1，y＝－2.所以n＝(1，－2，2).‎ 又＝(1，1，－1)，所以cos〈n，〉＝＝－.‎ 所以直线PB与平面PCD所成角的正弦值为.--------------12分 ‎20.解　(1)由题意得：--------------2分 解得：,所以椭圆C1的方程为＋y2＝1. --------------4分 ‎(2)设A(x1，y1)，B(x2，y2)，D(x0，y0).由题意知直线l1的斜率存在，不妨设其为k，‎ 则直线l1的方程为y＝kx－1. --------------5分[]‎ 又圆C2：x2＋y2＝4，故点O到直线l1的距离d＝，‎ 所以|AB|＝2＝2.--------------7分 又l2⊥l1，故直线l2的方程为x＋ky＋k＝0.‎ 由消去y，整理得(4＋k2)x2＋8kx＝0，--------------8分 故x0＝－.所以由弦长公式得|PD|＝.--------------10分 设△ABD的面积为S，则S＝|AB|·|PD|＝，‎ 所以S＝≤＝，‎ 当且仅当k＝±时取等号.所以所求直线l1的方程为y＝±x－1. --------------12分 ‎21.解：（1）由题意，≥0在上恒成立，即．1分 ‎ ∵θ∈（0，π），∴．故在上恒成立，-------- 2分 ‎ 只须，即，只有．结合θ∈（0，π），得--------4分 ‎（2）由（1），=．所以． ‎ ‎∵在其定义域内为单调函数，‎ ‎∴或者在[1，＋∞）恒成立．‎ ‎ 等价于，即，‎ ‎ 而 ，（）max=1，∴． --------6分 等价于，即在[1，＋∞）恒成立，‎ 而∈（0，1]，．综上，m的取值范围是．-------- 9分 ‎（3）．‎ 当时，，，，所以在[1，e]上不存在一个使得成立． ‎ 当时，． ‎ 因为，所以，，所以在恒成立．‎ 故在上单调递增，，只要，‎ 解得故的取值范围是．-------- 12分 ‎22.解:（1)由得曲线的普通方程为------------2分 把，代入--------------4分 化简得曲线的极坐标方程为 --------------5分 ‎ ‎（2）依题意可设,，曲线的极坐标方程为 ‎ 将,代入曲线的极坐标方程得，解得--------------8分 将,代入曲线的极坐标方程得 所以 ---------------------------10分 ‎23. 解(1）若恒成立，即……2分 由绝对值的三角不等式得，得 即，解得，所以M=4 ……5分 ‎（2）证明：由（Ⅰ）知，得……6分 所以有 即 ……10分