- 2021-06-11 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习教案: 解三角形应用举例
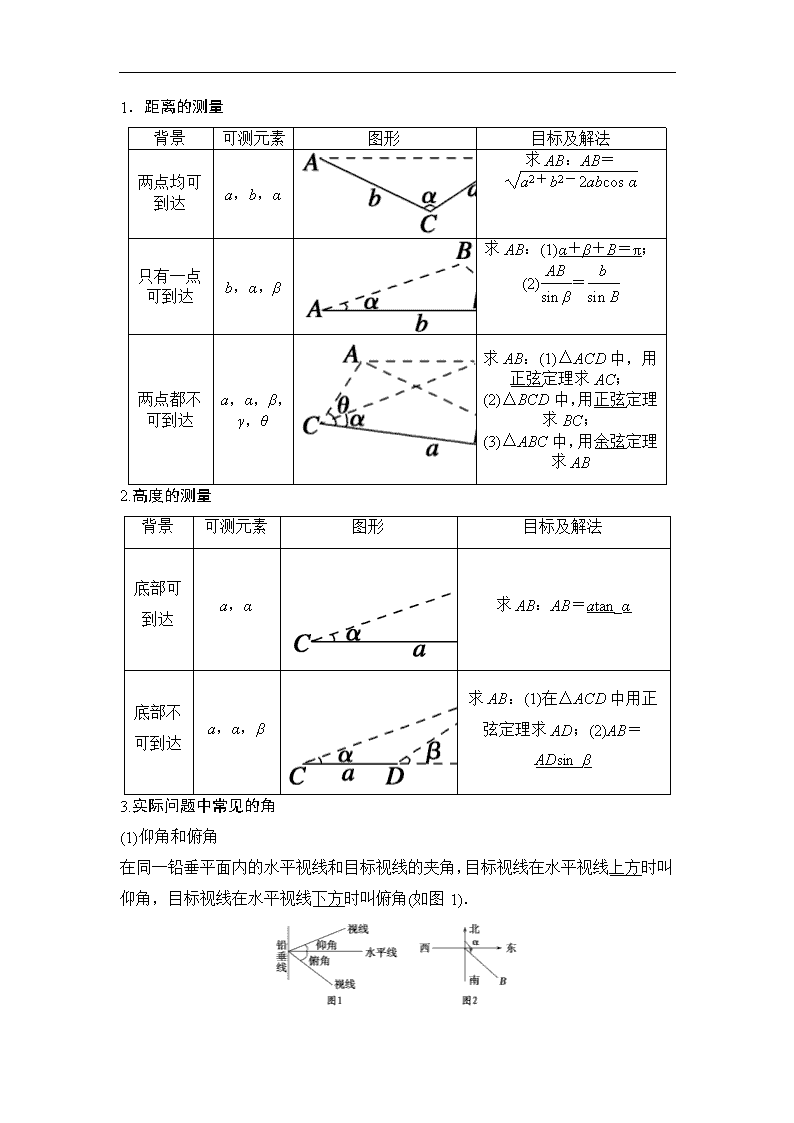
解三角形应用举例 主标题:解三角形应用举例 副标题:为学生详细的分析解三角形应用举例的高考考点、命题方向以及规律总结。 关键词:距离测量,高度测量,仰角,俯角,方位角,方向角 难度:3 重要程度:5 考点剖析: 能够运用正弦定理、余弦定理等知识解决一些与测量和几何计算有关的实际问题. 命题方向: 1.测量距离问题是高考的常考内容,既有选择、填空题,也有解答题,难度适中,属中档题. 2.高考对此类问题的考查常有以下两个命题角度: (1)测量问题; (2)行程问题. 规律总结: 1个步骤——解三角形应用题的一般步骤 2种情形——解三角形应用题的两种情形 (1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解. (2)实际问题经抽象概括后,已知量与未知量涉及到两个或两个以上的三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解. 2个注意点——解三角形应用题应注意的问题 (1)画出示意图后要注意寻找一些特殊三角形,如等边三角形、直角三角形、等腰三角形等,这样可以优化解题过程. (2)解三角形时,为避免误差的积累,应尽可能用已知的数据(原始数据),少用间接求出的量. 知 识 梳 理 1.距离的测量 背景 可测元素 图形 目标及解法 两点均可到达 a,b,α 求AB:AB= 只有一点可到达 b,α,β 求AB:(1)α+β+B=π;(2)= 两点都不可到达 a,α,β,γ,θ 求AB:(1)△ACD中,用正弦定理求AC; (2)△BCD中,用正弦定理求BC; (3)△ABC中,用余弦定理求AB 2.高度的测量 背景 可测元素 图形 目标及解法 底部可到达 a,α 求AB:AB=atan_α 底部不可到达 a,α,β 求AB:(1)在△ACD中用正弦定理求AD;(2)AB=ADsin_β 3.实际问题中常见的角 (1)仰角和俯角 在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫仰角,目标视线在水平视线下方时叫俯角(如图1). (2)方位角 从正北方向起按顺时针转到目标方向线之间的水平夹角叫做方位角.如B点的方位角为α(如图2). (3)方向角:正北或正南方向线与目标方向线所成的锐角,如南偏东30°,北偏西45°等. (4)坡度:坡面与水平面所成的二面角的度数.查看更多