2019高三数学理北师大版一轮课时分层训练66　古典概型

2019高三数学理北师大版一轮课时分层训练66　古典概型

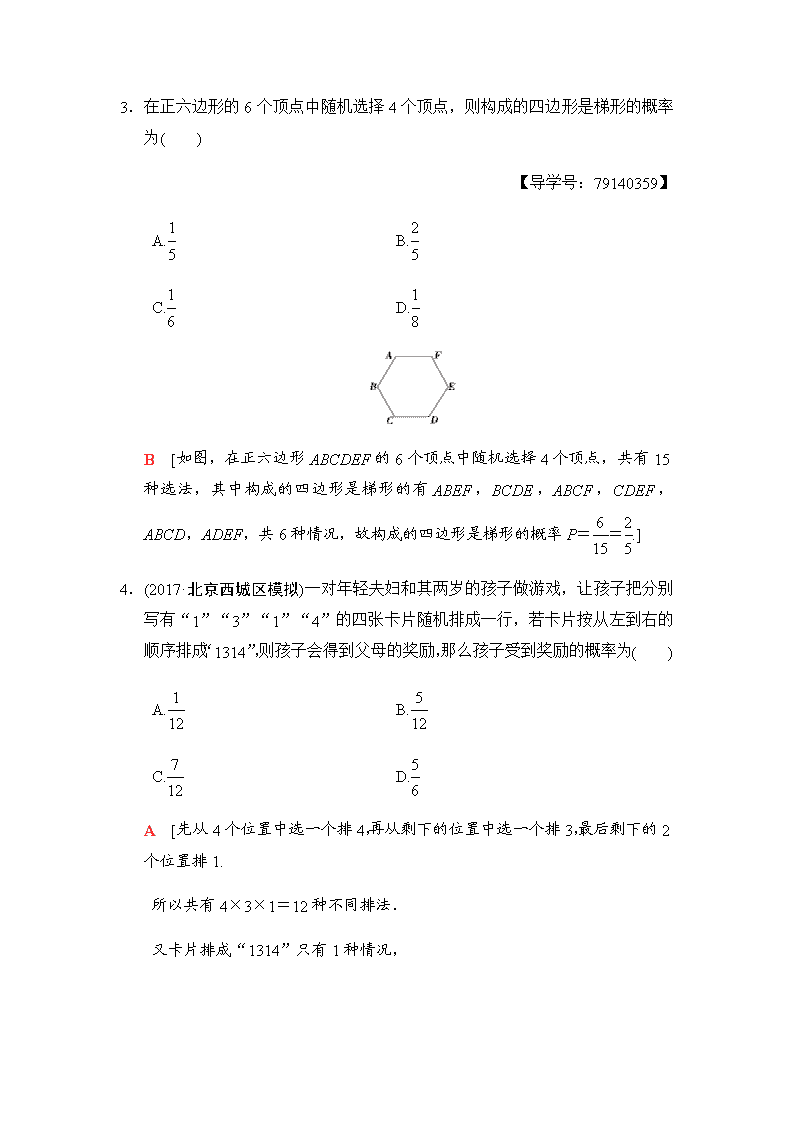
课时分层训练(六十六)　古典概型 ‎(对应学生用书第328页)‎ A组　基础达标 一、选择题 ‎1．(天津十二区县联考(一))若从2个海滨城市和2个内陆城市中随机选2个去旅游，那么恰好选1个海滨城市的概率是(　　)‎ A.　　　 B. C. D. B　[设2个海滨城市分别为A，B,2个内陆城市分别为a，b，从4个城市中选择2个去旅游有(A，B)，(A，a)，(A，b)，(B，a)，(B，b)，(a，b)，共6种不同的选法，其中满足恰好有1个海滨城市的有(A，a)，(A，b)，(B，a)，(B，b)，共4种不同的选法，则所求概率为＝，故选B.]‎ ‎2．(2015·全国卷Ⅰ)如果3个正整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数，从1,2,3,4,5中任取3个不同的数，则这3个数构成一组勾股数的概率为(　　)‎ A. B. C. D. C　[从1,2,3,4,5中任取3个不同的数共有如下10个不同的结果：(1,2,3)，(1,2,4)，(1,2,5)，(1,3,4)，(1,3,5)，(1,4,5)，(2,3,4)，(2,3,5)，(2,4,5)，(3,4,5)，其中勾股数只有(3,4,5)，所以概率为.故选C.]‎ ‎3．在正六边形的6个顶点中随机选择4个顶点，则构成的四边形是梯形的概率为(　　) ‎ ‎【导学号：79140359】‎ A. B. C. D. B　[如图，在正六边形ABCDEF的6个顶点中随机选择4个顶点，共有15种选法，其中构成的四边形是梯形的有ABEF，BCDE，ABCF，CDEF，ABCD，ADEF，共6种情况，故构成的四边形是梯形的概率P＝＝.]‎ ‎4．(2017·北京西城区模拟)一对年轻夫妇和其两岁的孩子做游戏，让孩子把分别写有“1”“3”“1”“4”的四张卡片随机排成一行，若卡片按从左到右的顺序排成“1314”，则孩子会得到父母的奖励，那么孩子受到奖励的概率为(　　)‎ A. B. C. D. A　[先从4个位置中选一个排4，再从剩下的位置中选一个排3，最后剩下的2个位置排1.‎ 所以共有4×3×1＝12种不同排法．‎ 又卡片排成“1314”只有1种情况，‎ 故所求事件的概率P＝.]‎ ‎5.某车间共有12名工人，随机抽取6名作为样本，他们某日加工零件个数的茎叶图如图1053所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．要从这6人中，随机选出2人参加一项技术比赛，选出的2人至少有1人为优秀工人的概率为(　　)‎ 图1053‎ A. B. C. D. C　[由已知得，样本均值为＝＝22，故优秀工人只有2人．‎ 故所求概率为P＝＝＝，故选C.]‎ 二、填空题 ‎6．(2018·南京、盐城、连云港二模)某校有三个兴趣小组，甲、乙两名学生每人选择其中一个参加，且每人参加每个兴趣小组的可能性相同，则甲、乙不在同一个兴趣小组的概率为________．‎ 　[甲、乙两名学生参加兴趣小组的结果共有9种，其中甲、乙不在同一个兴趣小组的结果有6种，故所求的概率为＝.]‎ ‎7．从n个正整数1,2,3，…，n中任意取出两个不同的数，若取出的两数之和等于5的概率为，则n＝________. ‎ ‎【导学号：79140360】‎ ‎8　[因为5＝1＋4＝2＋3，‎ 所以＝，解得n＝8(舍去n＝－7)．]‎ ‎8．(2016·江苏高考)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次，则出现向上的点数之和小于10的概率是________．‎ 　[将一颗质地均匀的骰子先后抛掷2次，所有等可能的结果有(1,1)，(1,2)，(1,3)，(1,4)，(1,5)，(1,6)，(2,1)，(2,2)，…，(6,6)，共36种情况．设事件A＝“出现向上的点数之和小于10”，其对立事件＝“出现向上的点数之和大于或等于10”，包含的可能结果有(4,6)，(5,5)，(5,6)，(6,4)，(6,5)，(6,6)，共6种情况．所以由古典概型的概率公式，得P()＝＝，所以P(A)＝1－＝.]‎ 三、解答题 ‎9．(2017·山东高考)某旅游爱好者计划从3个亚洲国家A1，A2，A3和3个欧洲国家B1，B2，B3中选择2个国家去旅游．‎ ‎(1)若从这6个国家中任选2个，求这2个国家都是亚洲国家的概率；‎ ‎(2)若从亚洲国家和欧洲国家中各任选1个，求这2个国家包括A1但不包括B1的概率．‎ ‎[解]　(1)由题意知，从6个国家中任选两个国家，其一切可能的结果组成的基本事件有：{A1，A2}，{A1，A3}，{A2，A3}，{A1，B1}，{A1，B2}，{A1，B3}，{A2，B1}，{A2，B2}，{A2，B3}，{A3，B1}，{A3，B2}，{A3，B3}，{B1，B2}，{B1，B3}，{B2，B3}，共15个．‎ 所选两个国家都是亚洲国家的事件所包含的基本事件有：{A1，A2}，{A1，‎ A3}，{A2，A3}，共3个，则所求事件的概率为P＝＝.‎ ‎(2)从亚洲国家和欧洲国家中各任选一个，其一切可能的结果组成的基本事件有：{A1，B1}，{A1，B2}，{A1，B3}，{A2，B1}，{A2，B2}，{A2，B3}，{A3，B1}，{A3，B2}，{A3，B3}，共9个．‎ 包括A1但不包括B1的事件所包含的基本事件有：{A1，B2}，{A1，B3}，共2个，则所求事件的概率为P＝.‎ ‎10．移动公司在国庆期间推出4G套餐，对国庆节当日办理套餐的客户进行优惠，优惠方案如下：选择套餐1的客户可获得优惠200元，选择套餐2的客户可获得优惠500元，选择套餐3的客户可获得优惠300元．国庆节当天参与活动的人数统计结果如图1054所示，现将频率视为概率．‎ 图1054‎ ‎(1)求从中任选1人获得优惠金额不低于300元的概率；‎ ‎(2)若采用分层抽样的方式从参加活动的客户中选出6人，再从该6人中随机选出2人，求这2人获得相等优惠金额的概率．‎ ‎[解]　(1)设事件A为“从中任选1人获得优惠金额不低于300元”，则P(A)＝＝.‎ ‎(2)设事件B为“从这6人中选出2人，他们获得相等优惠金额”，由题意按分层抽样方式选出的6人中，获得优惠200元的有1人，获得优惠500元的有3人，获得优惠300元的有2人，分别记为a1，b1，b2，b3，c1，c2，从中选出2人的所有基本事件如下：a1b1，a1b2，a1b3，a1c1，a1c2，b1b2，b1b3，b1c1，b1c2，b2b3，b2c1，b2c2，b3c1，b3c2，c1c2，共15个．‎ 其中使得事件B成立的有b1b2，b1b3，b2b3，c1c2，共4个．‎ 则P(B)＝.‎ B组　能力提升 ‎11．(2017·西安调研)安排甲、乙、丙、丁四人参加周一至周六的公益活动，每天只需一人参加，其中甲参加三天活动，乙、丙、丁每人参加一天，那么甲连续三天参加活动的概率为(　　)‎ A. B. C. D. B　[由题意，甲连续三天参加活动的所有情况为：第1～3天，第2～4天，第3～5天，第4～6天，共4种．‎ 故所求事件的概率P＝＝.]‎ ‎12．现有7名数理化成绩优秀者，分别用A1，A2，A3，B1，B2，C1，C2表示，其中A1，A2，A3的数学成绩优秀，B1，B2的物理成绩优秀，C1，C2的化学成绩优秀．从中选出数学、物理、化学成绩优秀者各1名，组成一个小组代表学校参加竞赛，则A1和B1不全被选中的概率为________．‎ 　[从这7人中选出数学、物理、化学成绩优秀者各1名，所有可能的结果组成的12个基本事件为：(A1，B1，C1)，(A1，B1，C2)，(A1，B2，C1)，(A1，B2，C2)，(A2，B1，C1)，(A2，B1，C2)，(A2，B2，C1)，(A2，B2，C2)，(A3，B1，C1)，(A3，B1，C2)，(A3，B2，C1)，(A3，B2，C2)．‎ 设“A1和B1不全被选中”为事件N，则其对立事件表示“A1和B1全被选中”，由于＝{(A1，B1，C1)，(A1，B1，C2)}，所以P()＝＝ ‎，由对立事件的概率计算公式得P(N)＝1－P()＝1－＝.]‎ ‎13．袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为，现有甲、乙两人从袋中轮流摸球，甲先取，乙后取，然后甲再取，…，取后不放回，直到两人中有一人取到白球时即终止，每个球在每一次被取出的机会是等可能的. ‎ ‎【导学号：79140361】‎ ‎(1)求袋中原有白球的个数；‎ ‎(2)求取球2次即终止的概率；‎ ‎(3)求甲取到白球的概率．‎ ‎[解]　(1)设袋中原有n个白球，从袋中任取2个球都是白球的结果数为C，从袋中任取2个球的所有可能的结果数为C.‎ 由题意知从袋中任取2球都是白球的概率P＝＝，则n(n－1)＝6，解得n＝3(舍去n＝－2)，即袋中原有3个白球．‎ ‎(2)设事件A为“取球2次即终止”．取球2次即终止，即乙第一次取到的是白球而甲取到的是黑球，‎ P(A)＝＝＝.‎ ‎(3)设事件B为“甲取到白球”，“第i次取到白球”为事件Ai，i＝1,2,3,4,5，因为甲先取，所以甲只可能在第1次，第3次和第5次取到白球．‎ 所以P(B)＝P(A1∪A3∪A5)＝P(A1)＋P(A3)＋P(A5)＝＋＋＝＋＋＝.‎