- 2021-06-11 发布 |
- 37.5 KB |
- 3页
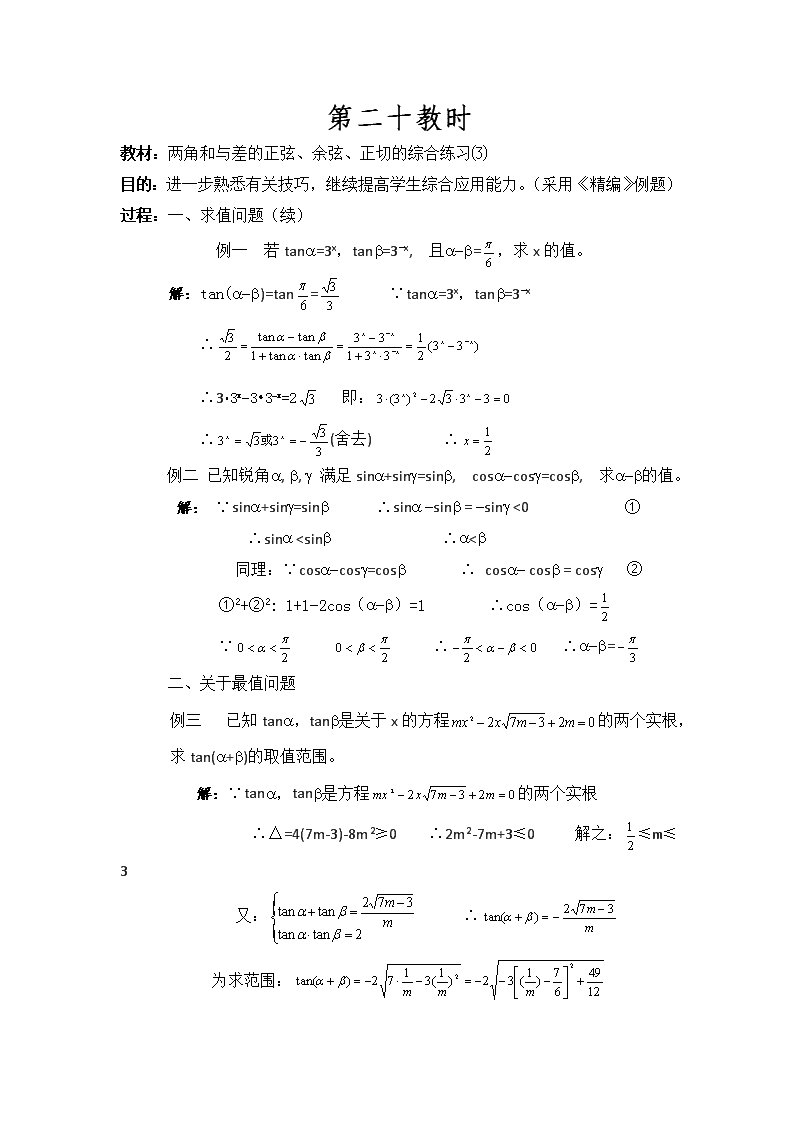
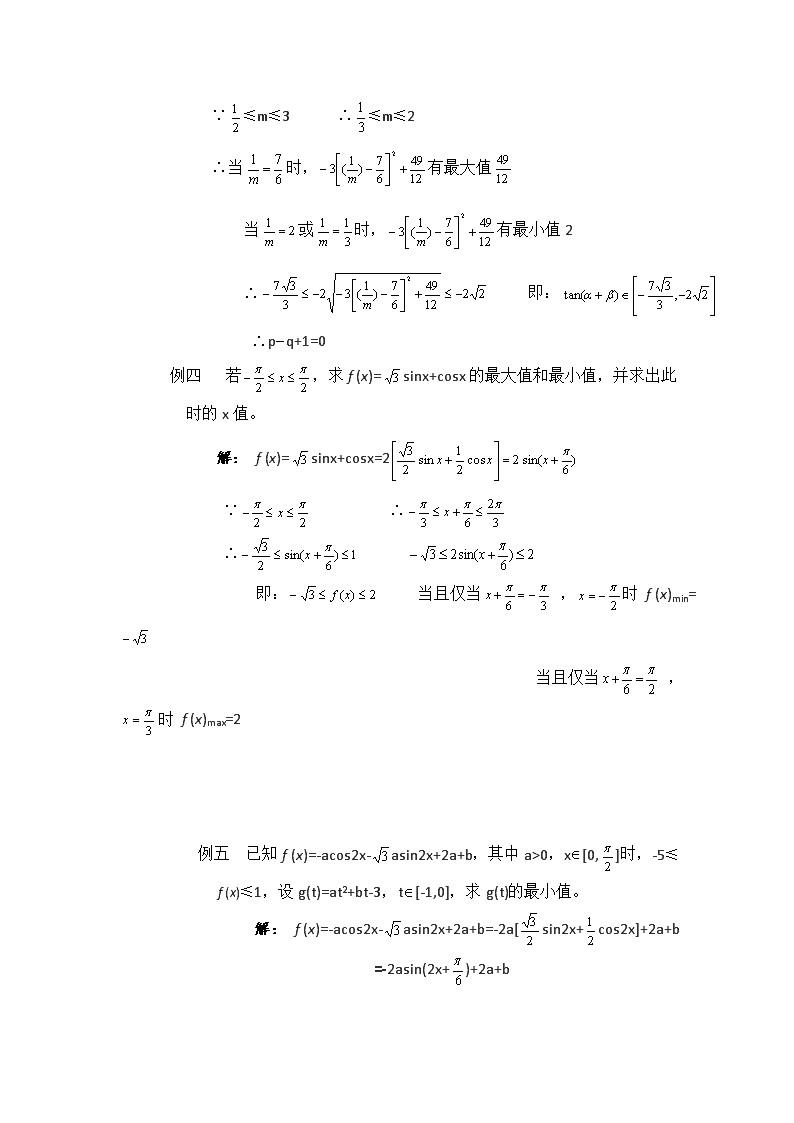

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2018届一轮复习苏教版两角和与差的正弦、余弦、正切的综合练习⑶教案
第二十教时 教材:两角和与差的正弦、余弦、正切的综合练习⑶ 目的:进一步熟悉有关技巧,继续提高学生综合应用能力。(采用《精编》例题) 过程:一、求值问题(续) 例一 若tana=3x,tanb=3-x, 且a-b=,求x的值。 解:tan(a-b)=tan= ∵tana=3x,tanb=3-x ∴ ∴3•3x-3•3-x=2 即: ∴(舍去) ∴ 例二 已知锐角a, b, g 满足sina+sing=sinb, cosa-cosg=cosb, 求a-b的值。 解: ∵sina+sing=sinb ∴sina -sinb = -sing <0 ① ∴sina查看更多