江苏省泗阳中学、盱眙中学2013届高三12月联考数学试题

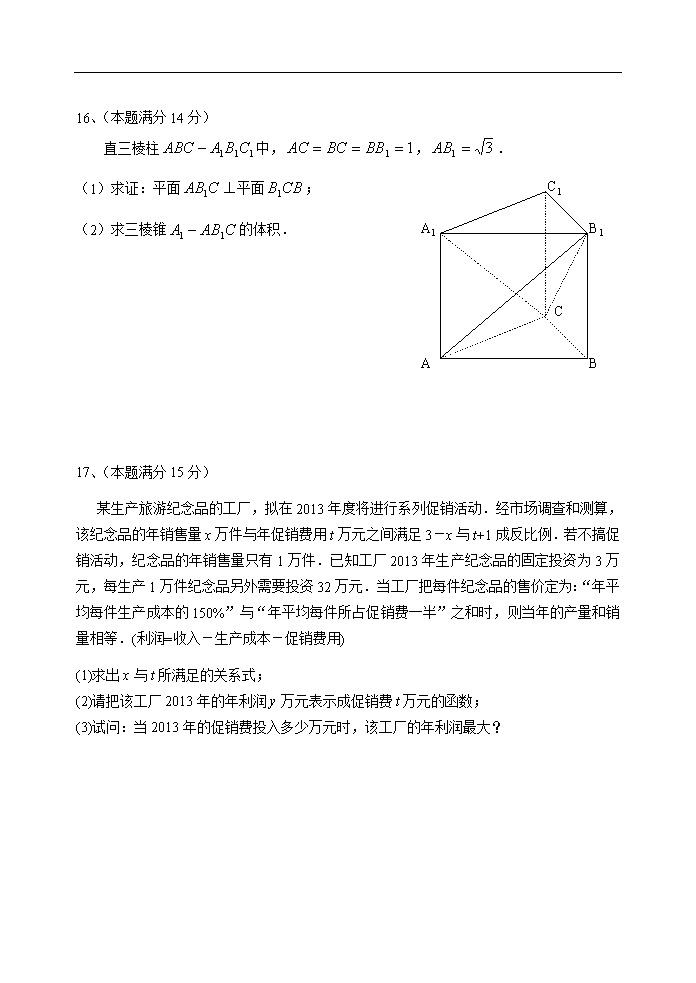
江苏省泗阳中学、盱眙中学2013届高三12月联考数学试题

江苏省泗阳中学、盱眙中学2013届高三联考数学试题 ‎ 数 学Ⅰ 2012、12‎ ‎ 命题单位:江苏省盱眙中学 ‎★祝考试顺利★ ‎ 注　意　事　项 考生在答题前请认真阅读本注意事项及各题答题要求：‎ ‎1．本试卷共4页，均为非选择题（第1题～第20题，共20题）。本卷满分为160分。考试时间为120分钟。考试结束后，请将本试卷和答题卡一并交回。‎ ‎2．答题前，请您务必将自己的姓名、考试证号用‎0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。‎ ‎3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。‎ ‎4．作答试题必须用‎0.5毫米黑色墨水的签字笔在答题卡的指定位置作答，在其它位置作答一律无效。‎ ‎5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗。‎ 一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．‎ ‎1、已知全集，集合，集合，则＝ ☆ ．‎ ‎2、某校高中生有900人，其中高一年级300人，高二年级200人，高三年级400人，现采取分层抽样法抽取容量为45人的样本，那么从高三年级抽取的人数为 ☆ ；‎ ‎3、若复数(a+i)(1—2 i)( i是虚数单位)是纯虚数，则实数a= ☆ ；‎ Read x If x≤0 Then ‎ ‎←‎ Else ‎←‎ End If Print ‎ ‎（第4题图）‎ ‎4、以如图所示伪代码：‎ 根据以上伪代码，则= ☆ . ‎ ‎5、函数的定义域是 ☆ ； ‎ ‎6、若随机向一个边长为2的正方形内丢一粒豆子，则豆子落在此正方形内切圆内的概率为　　 ☆ 　； ‎ ‎7、设a，b为两个不重合的平面，l，m，n为两两不重合的直线，给出下列四个命题：‎ ‎①若a∥b，lÌa，则l∥b； ②若mÌa，nÌa，m∥b，n∥b，则a∥b；　 ‎ ‎③若l∥a，l⊥b，则a⊥b； ④若m、n是异面直线，m∥a，n∥a，且l⊥m，l⊥n ‎，则l⊥a.其中真命题的序号是 ☆ ； ‎ ‎8、两个正数a、b的等差中项是，一个等比中项是，且则双曲线的离心率为 ☆ ； ‎ ‎9、已知函数在上是减函数，则实数的取值范围是 ☆ ；‎ ‎10、在等差数列中，若它的前n项和有最大值，则使取得最小正数 的 ☆ ；‎ ‎11、在直角中，两条直角边分别为，斜边和斜边上的高分别为，则的取值范围是 ☆ ．‎ ‎12、直线与圆相交于，两点（其中是实数），且是直角三角形（是坐标原点），则点与点之间距离的最大值为 ☆ ；‎ A C B D E ‎13、如图，△中,,=,，‎ 延长到，使，当点在线段 上移动时，若，则 的最大值是 ☆ ；‎ ‎14、在平面直角坐标系中，点集，，则点集所表示的区域的面积为 ☆ ．‎ 二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．‎ ‎15、（本小题满分14分）‎ 在中，内角的对边分别为已知成等比数列，.‎ ‎(1)若求的值；‎ ‎(2)求的值．‎ ‎16、（本题满分14分）‎ 直三棱柱中，，．‎ A B C C1‎ A1‎ B1‎ ‎（1）求证：平面平面；‎ ‎（2）求三棱锥的体积．‎ ‎17、（本题满分15分）‎ 某生产旅游纪念品的工厂，拟在2013年度将进行系列促销活动．经市场调查和测算，该纪念品的年销售量x万件与年促销费用t万元之间满足3－x与t+1成反比例．若不搞促销活动，纪念品的年销售量只有1万件．已知工厂2013年生产纪念品的固定投资为3万元，每生产1万件纪念品另外需要投资32万元．当工厂把每件纪念品的售价定为：“年平均每件生产成本的150%”与“年平均每件所占促销费一半”之和时，则当年的产量和销量相等．(利润=收入－生产成本－促销费用)‎ ‎(1)求出x与t所满足的关系式；‎ ‎(2)请把该工厂2013年的年利润y万元表示成促销费t万元的函数；‎ ‎(3)试问：当2013年的促销费投入多少万元时，该工厂的年利润最大？‎ ‎18、（本题满分15分）‎ 设椭圆C：的左焦点为F，上顶点为A，过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q，且. ‎ ‎⑴求椭圆C的离心率； ‎ ‎⑵若过A、Q、F三点的圆恰好与直线l：相切，求椭圆C的方程.‎ F O A P Q y x ‎19、（本题满分16分）‎ 已知数列的首项（a是常数，且），（），数列的首项，（）。 ‎ ‎（1）证明：从第2项起是以2为公比的等比数列；‎ ‎（2）设为数列的前n项和，且是等比数列，求实数a的值；‎ ‎（3）当时，求数列的最小项。‎ ‎20、（本小题满分16分）‎ 已知函数（a为正实数）．‎ ‎(1) 设，试讨论的单调性；‎ ‎（2）设当时，‎ ‎（）若对任意，存在，使，求实数取值范围．‎ ‎() 对于任意都有，求的取值范围．‎ 江苏省泗阳中学、盱眙中学2013届高三联考数学试题 数学Ⅱ(附加题)‎ 注　意　事　项 考生在答题前请认真阅读本注意事项及各题答题要求：‎ ‎1．本试卷共2页，均为非选择题（第21题～第23题）。本卷满分为40分。考试时间为30分钟。考试结束后，请将本试卷和答题卡一并交回。‎ ‎2．答题前，请您务必将自己的姓名、考试证号用‎0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。‎ ‎3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。‎ ‎4．作答试题必须用‎0.5毫米黑色墨水的签字笔在答题卡的指定位置作答，在其它位置作答一律无效。‎ ‎5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗。‎ ‎21．[选做题]本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．‎ A．[选修4 - 1：几何证明选讲]（本小题满分10分）‎ 如图，已知：C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B点的切线相交于点D，E为CH中点，连接AE并延长交BD于点F，直线CF交直线AB于点G.‎ ‎（Ⅰ）求证：F是BD的中点；‎ ‎（Ⅱ）求证：CG是⊙O的切线．‎ B．[选修4 - 2：矩阵与变换]（本小题满分10分）‎ 求矩阵A=的逆矩阵；‎ C．[选修4 - 4：坐标系与参数方程]（本小题满分10分）‎ 求直线（）被曲线所截的弦长；‎ D．[选修4 - 5：不等式选讲]（本小题满分10分）‎ 已知a>0,b>0,c>0,abc=1,试证明：.‎ ‎【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．‎ ‎22．（本小题满分10分）‎ 某校从4名男教师和2名女教师中任选3人参加全县教育系统举行的“学习十八大精神”教育演讲赛。如果设随机变量表示所选3人中女教师的人数。求：‎ ‎ (1) 的分布列；(2) 的数学期望；(3) “所选3人中女教师人数”的概率。‎ ‎23．（本小题满分10分）‎ 已知多项式.‎ ‎（1）求及的值；‎ ‎（2）试探求对一切整数n，是否一定是整数？并证明你的结论．‎ 命题：盱眙中学数学组 江苏省泗阳中学、盱眙中学2013届高三联考数学 参 考 答 案 ‎1、{3，5}； 2、20； 3、—2； 4、； 5、； 6、； 7、①③④‎ ‎8、； 9、； 10、19； 11、； 12、； 13、； 14、；‎ ‎15、解：（1）成等比数列，……………………………2分 又，由余弦定理，‎ 得 ………………………………………………4分 即 ……………………………………7分 ‎（2）由，得 ……………………………………9分 由及正弦定理得…………………………………………10分 于是 ‎………………………………14分 ‎16、解：（1）直三棱柱ABC—A1B‎1C1中，BB1⊥底面ABC，‎ 则BB1⊥AB，BB1⊥BC，------------------------------------------------------------3分 又由于AC=BC=BB1=1，AB1=，则AB=，‎ 则由AC2+BC2=AB2可知，AC⊥BC，--------------------------------------------6分 又由上BB1⊥底面ABC可知BB1⊥AC，则AC⊥平面B1CB，‎ 所以有平面AB‎1C⊥平面B1CB；--------------------------------------------------9分 ‎（2）三棱锥A1—AB‎1C的体积．----------14分 ‎（注：还有其它转换方法请参照给分）‎ ‎17、解 (1)　设比例系数为k．由题知，有．…………………2分 又 ‎　．………………………………………………………4分 ‎　．………………………………………5分 ‎(2) 依据题意，可知工厂生产x万件纪念品的生产成本为万元，促销费用为t万元，则每件纪念品的定价为：()元／件．………………8分 于是，，进一步化简，得 ‎．……………………………………………………10分 因此，工厂2010年的年利润万元．‎ ‎(3) 由(2)知，‎ ‎　　……………14分 ‎ 所以，当2010年的促销费用投入7万元时，工厂的年利润最大，最大利润为42万元．……………………………………………………………………………………15分 ‎18、⑴解：设Q（x0，0），由F（-c，0） A（0，b）知 ‎ ………………………………………2分 设，‎ 得 因为点P在椭圆上，所以………………………………5分 整理得2b2=‎3ac，即2(a2－c2)=‎3ac，,故椭圆的离心率 e=………………8分 ‎⑵由⑴知， 于是F（－a，0） Q，‎ ‎△AQF的外接圆圆心为（a，0），半径r=|FQ|=a ………………………………10分 所以，解得a=2，∴c=1，b=，所求椭圆方程为………………15分 ‎19、解：（1）∵∴‎ ‎　　　(n≥2) …………3分 由得，，‎ ‎∵，∴ ，…………4分 即从第2项起是以2为公比的等比数列。…………5分 ‎（2） …………6分 当n≥2时，‎ ‎∵是等比数列, ∴(n≥2)是常数，‎ ‎∴‎3a+4=0，即 。…………10分 ‎（3）由（1）知当时，，………………11分 所以，…………12分 所以数列为‎2a+1，‎4 a，‎8 a—1，‎16 a，‎32 a +7，……‎ 显然最小项是前三项中的一项。…………13分 当时，最小项为‎8 a —1；‎ 当时，最小项为‎4 a或‎8 a—1；………14分 当时，最小项为‎4 a；‎ 当时，最小项为‎4 a或‎2 a +1；…………15分 当时，最小项为‎2 a +1。…………16分 ‎20、解：(1)函数的定义域为，因为，……1分 ‎ 令，可得，‎ ‎①当时，，由，可得，故此时函数在是增函数，同样可得在上是减函数； ………………………………………………3分 ‎②时，恒成立，故此时函数在是减函数；……………………4分 ‎③当，由，可得，故此时函数在是增函数，在上是减函数； ……………………………………………………………………5分 ‎（2） （）当时，由（1）可知在（0，1）上是减函数，在（1，2）上是增函数，……7分 所以对任意，有 由条件存在，使，所以．‎ 即存在，使，即在时有解，……………8分 亦即在时有解．‎ 由于为减函数，故其值域为，‎ 从而，即有 ，所以实数取值范围是． …………………………11分 ‎()不妨设，由函数在上是增函数，函数在是减函数，‎ 所以等价于，即．……13分 设 由于对任意，且，总有 故函数在是减函数（非严格单调递减），‎ 所以在上恒成立，由此易得，解得．…………16分 ‎21、（A）（Ⅰ）证:∵CH⊥AB，DB⊥AB，∴△AEH∽AFB，△ACE∽△ADF ‎∴，∵HE＝EC，∴BF＝FD ∴ F是BD中点.…………………(5分)‎ ‎（Ⅱ）∵AB是直径，∴∠ACB＝90°∴∠BCF=∠CBF=90°－∠CBA=∠CAB=∠ACO ‎∴∠OCF=90°，∴CG是⊙O的切线……………………………………(10分)‎ ‎（B）解：设逆矩阵为，则由 得，解得a=2,b= —3,c= —1，d=2，所以…………10分 ‎（C）解：将方程,分别化为普通方程：‎ ‎，……………………………………………(5分)‎ ‎……(10分)‎ ‎（D）解: 证明：由，‎ 所以 同理： ， ‎ 相加得：左³…………………………………(10分)‎ ‎22、解析: (1)　易知可能取的值为．‎ 所以，的分布列为 ‎0‎ ‎1‎ ‎2‎ P ‎ ‎ ‎………………………6分 ‎ (2) 的数学期望为： ； ………………………8分 ‎(3) “所选3人中女教师人数”的概率为： 。………10分 ‎23、解：（1）； ； …………………………………………2分 ‎（2）对一切整数n，是否一定是整数.证明如下：‎ ‎（）先用数学归纳法证明：对一切正整数n，是整数；‎ ‎①当n=1时，,结论成立；‎ ‎②假设当n=k（k≥1，k∈N*）时，结论成立，即是整数，则当n=k+1时，‎ ‎=‎ 根据假设是整数，而显然是整数.‎ ‎∴是整数，从而当当n=k+1时，结论也成立.‎ 由①、②可知对对一切正整数n，是整数. …………………………………7分 ‎（）当n=0时，是整数.……………………………………………………8分 ‎()当n为负整数时，令n= —m，则m是正整数，由（1）是整数，‎ 所以 ‎=是整数.‎ 综上，对一切整数n，一定是整数.………………………………………10分