- 2021-06-11 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
安徽省东至县2013届高三12月“一模”数学(理)试题
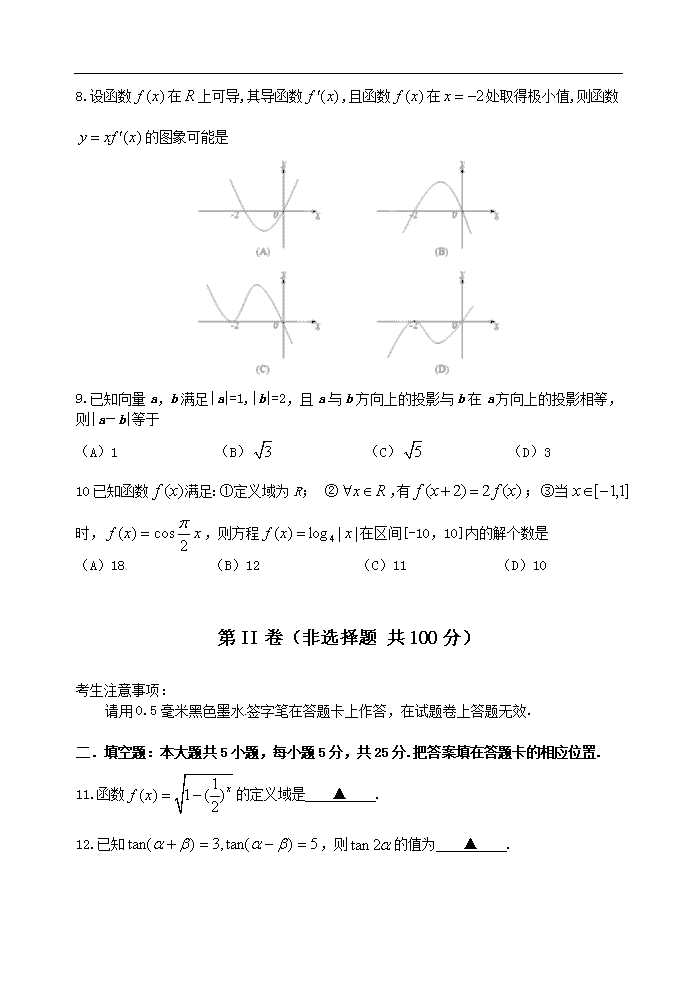
安徽省东至县2013届高三“一模”理科数学试卷 第Ⅰ卷(选择题 共50分) 一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。 1.已知集合,,则为 A. B. C. D. 2.若,则下列不等式成立的是 A. B. C. D. 3.在等差数列{an}中,已知a4+a8=16,则该数列前11项和S11= A.58 B.88 C.143 D.176 4.函数(其中)的图象如图所示,为了得到的图象,则只需将的图象 A.向右平移个长度单位 B.向右平移个长度单位 C.向左平移个长度单位 D.向左平移个长度单位 5. 已知,则是第( )象限角: A. 第一象限 B .第二象限 C.第三象限 D. 第四象限 6.已知为等比数列,,,则 A.7 B.5 C.-5 D.-7 7.函数的最大值与最小值之和为 A. B.0 C.-1 D. 8.设函数在上可导,其导函数,且函数在处取得极小值,则函数 的图象可能是 9.已知向量a,b满足|a|=1,|b|=2,且a与b方向上的投影与b在a方向上的投影相等,则|a-b|等于 (A)1 (B) (C) (D)3 10已知函数满足:①定义域为R; ②,有; ③当时,,则方程在区间[-10,10]内的解个数是 (A)18 (B)12 (C)11 (D)10 [来源:学科网ZXXK][来源:学*科*网Z*X*X*K] 第II卷(非选择题 共100分) 21世纪教育网 考生注意事项: 请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效. 二.填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置. 11.函数的定义域是 ▲ . 12.已知,则的值为 ▲ . 13.若变量x、y满足,若的最大值为,则 ▲ . 14.若函数在其定义域内的一个子区间内不是单调函数,则实数k 的取值范围是 ▲ . 15. 若直角坐标平面内M、N两点满足: ①点M、N都在函数f(x)的图像上;[来源:学+科+网Z+X+X+K] ②点M、N关于原点对称,则称这两点M、N是函数f(x)的一对“靓点”。 已知函数则函数f(x)有 ▲ 对“靓点”。 三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.解答写在答题卡的制定区域内. 16. (本小题满分12分) 已知函数的定义域为A,函数的值域为B. (I)求; (II)若,且,求实数的取值范围. 17. (本小题满分12分)已知为等差数列,且. (I)求数列的通项公式; (II)的前项和为,若成等比数列,求正整数的值 18(本小题满分12分) 已知函数. (I)求的最小正周期;www.zxxk.com (Ⅱ)若将的图象按向量=(,0)平移得到函数g(x)的图象,求函数g(x)的解析式,并求g(x)的最大值和最小值. 19.(本小题满分13分) 中,分别是角A,B,C的对边,已知 满足,且 (1)求角A的大小; (2)求的值 20.本小题满分13分) 某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交元()的管理费,预计当每件产品的售价为元()时,一年的销售量为万件. (1)求分公司一年的利润L(万元)与每件产品的售价(元)的函数关系式; (2)当每件产品的售价为多少元时,分公司一年的利润L最大?并求出L的最大值 21.(本题满分13分). 已知函数 (1)若曲线在点处的切线与直线垂直,求函数的单调区间; (2)若对都有成立,试求实数a的取值范围; (3)记,当a=1时,函数在区间上有两个零点,求实数b的取值范围. 数学(理科)试卷答案 阅卷老师请注意:阅卷前请对答案进行审核 选择题 1、选 . , 2、选. , 3、选. 4、选. 由得,。又, 5、选. ,,在第四象限 6、选. , , 7、选. , 8、选. , 9、选. 易得 10、选. 二、填空题 11、 12、 13、 14、 15、1对 三、解答题: 16. 解:(Ⅰ)由题意得: ……………………………2分 ……………………………………………………4分 ……………………………………………………………6分 (II)由(1)知:,又 (1)当时,a<1,,满足题意 …………………8分 (2)当即时,要使,则 …………10分 解得 ………………………………………………………11分 综上, ………………………………………………12分 17.解:(I)设数列的公差为d,由题意得, 解得: …………………………………………………3分 所以 …………………5分 (II)由(I)可得: ……8分 因成等比数列,所以 从而,即 ………………………10分 解得:(舍去),因此. …………………12分 [来源:学,科,网Z,X,X,K] 18. .解:(I)…………………2分 =…………………………………………4分 所以的最小正周期为……………………………………………………5分 (Ⅱ)∵将将的图象按向量=(,0)平移,得到函数的图象. ∴…………………9分 ∵………………………………………10分 ∴当取得最大值2.………11分 当取得最小值—1.…12分 19. 解⑴ 即 ………………5分 ⑵ 而 ………………9分 与 可得 …………………………11分 ………13分 20(1)分公司一年的利润L(万元)与售价的函数关系式为: ………………………4分(少定义域去1分) (2) 令得或(不合题意,舍去)……………………6分 ∵,∴在两侧的值由正变负.-----8分 所以(1)当即时, ……………………………10分 (2)当即时, , 所以 ……………………………………12分 答:若,则当每件售价为9元时,分公司一年的利润L最大,最大值(万元);若,则当每件售价为元时,分公司一年的利润L最大,最大值为(万元).……………13分 21.解: (1) 直线的斜率为1. 函数的定义域为,, 所以,解得 ………2分 所以, ,得x>2; 得0查看更多
相关文章
- 当前文档收益归属上传用户