2020高中数学第四章函数应用4

2020高中数学第四章函数应用4

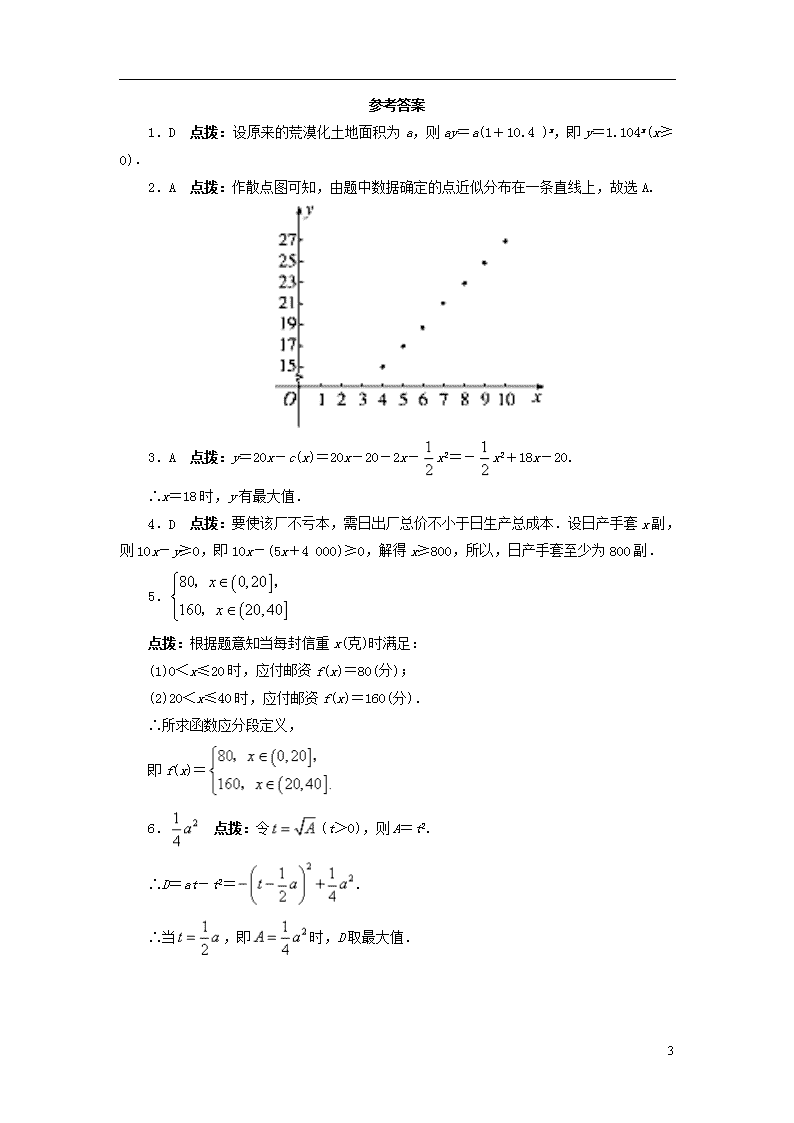
‎4.2 实际问题的函数建模 基础巩固 ‎1．在我国大西北，某地区荒漠化土地面积每年平均比上一年增长10.4 ，专家预测经过x年可能增长为原来的y倍，则函数y＝f(x)的图像大致为(　　)．‎ ‎2．下表是函数值y随自变量x变化的一组数据，由此判断它最可能的函数模型是(　　)．‎ x ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ y ‎15‎ ‎17‎ ‎19‎ ‎21‎ ‎23‎ ‎25‎ ‎27‎ A．一次函数模型 B．二次函数模型 C．指数函数模型 D．对数函数模型 ‎3．生产一定数量商品的全部费用称为生产成本，它可以表示为商品数量的函数，现知一企业生产某种商品的数量为x件时的成本函数为c(x)＝20＋2x＋(万元)，若售出一件商品收入是20万元，那么该企业为获取最大利润，应生产这种商品的数量为(　　)．‎ A．18件 B．36件 C．22件 D．9件 ‎4．某厂日产手套总成本y(元)与手套日产量x(副)的关系式为y＝5x＋4 000，而手套出厂价格为每副10元，则该厂为了不亏本，日产手套至少为(　　)．‎ A．200副 B．400副 C．600副 D．800副 ‎5．在国内投寄信，每封信不超过‎20克重付邮资80分，每封信超过‎20克重而不超过‎40克重付邮资160分，将每封信的应付邮资(分)表示成为信重x(0＜x≤40)克的函数，其表达式为f(x)＝________.‎ ‎6．“好酒也怕巷子深”，许多著名品牌是通过广告宣传进入消费者视线的．已知某品牌商品靠广告销售的收入R与广告费A之间满足关系 (a为常数)，广告效应为.那么精明的商人为了取得最大广告效应，投入广告费应为________．‎ ‎7．为了预防流感，某学校对教室用药熏消毒法进行消毒．已知药物释放过程中，室内每立方米空气中的含药量y(毫克)与时间t (小时)成正比．药物释放完毕后，y与t的函数关系式为(a为常数)，如图所示，根据图中提供的信息，回答下列问题：‎ 5‎ ‎(1)从药物释放开始，每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为________；‎ ‎(2)据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室，那么从药物释放开始，至少需要经过________小时，学生才能回到教室．‎ 能力提升 ‎8．某公司生产一种电子仪器的固定成本为20 000元，每生产一台仪器需要增加投入100元，已知总收益满足函数：R(x)＝其中x是仪器的月产量．‎ ‎(1)将利润y(元)表示为月产量x(台)的函数；‎ ‎(2)当月产量为何值时，公司所获得利润最大？最大利润是多少？(总收益＝总成本＋利润)‎ ‎9．某城市有甲、乙两家乒乓球俱乐部，两家设备和服务都很好，但收费方式不同．甲俱乐部每张球台每小时5元；乙家按月计费，一个月中30小时以内(含30小时)每张球台90元，超过30小时的部分每张球台每小时2元．小张准备下个月从这两家中的一家租一张球台开展活动，其活动时间不少于15小时，也不超过40小时．‎ ‎(1)设在甲俱乐部租一张球台开展活动x小时的收费为f(x)元(15≤x≤40)，在乙俱乐部租一张球台开展活动x小时的收费为g(x)元(15≤x≤40)．试求f(x)和g(x)．‎ ‎(2)问：小张选择哪家俱乐部比较合算？为什么？‎ 5‎ 参考答案 ‎1．D　点拨：设原来的荒漠化土地面积为a，则ay＝a(1＋10.4 )x，即y＝1.104x(x≥0)．‎ ‎2．A　点拨：作散点图可知，由题中数据确定的点近似分布在一条直线上，故选A.‎ ‎3．A　点拨：y＝20x－c(x)＝20x－20－2x－x2＝－x2＋18x－20.‎ ‎∴x＝18时，y有最大值．‎ ‎4．D　点拨：要使该厂不亏本，需日出厂总价不小于日生产总成本．设日产手套x副，则10x－y≥0，即10x－(5x＋4 000)≥0，解得x≥800，所以，日产手套至少为800副．‎ ‎5．‎ 点拨：根据题意知当每封信重x(克)时满足：‎ ‎(1)0＜x≤20时，应付邮资f(x)＝80(分)；‎ ‎(2)20＜x≤40时，应付邮资f(x)＝160(分)．‎ ‎∴所求函数应分段定义，‎ 即f(x)＝‎ ‎6．　点拨：令(t＞0)，则A＝t2.‎ ‎∴D＝at－t2＝.‎ ‎∴当，即时，D取最大值．‎ 5‎ ‎7．(1)‎ ‎(2)0.6‎ 点拨：(1)因为药物释放过程中，室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比，则设函数为y＝ t( ＞0)，将点(0.1,1)代入y＝ x，可得 ＝10，所以y＝10t；又因为药物释放完毕后，y与t的函数关系式为，将点(0.1,1)代入，得a＝0.1，故所求的函数关系式为)‎ ‎(2)由，得t＝0.6，‎ 即至少需要经过0.6小时后，学生才能回到教室．‎ ‎8．解：(1)由题设，总成本为20 000＋100x，‎ 则 ‎(2)当0≤x≤400时，y＝(x－300)2＋25 000，‎ 当x＝300时，ymax＝25 000；‎ 当x＞400时，y＝60 000－100x是减函数，‎ 则y＜60 000－100×400＝20 000＜25 000.‎ 所以，当x＝300时，有最大利润25 000元．‎ ‎9．解：(1)由题意得f(x)＝5x(15≤x≤40)，‎ 若在乙俱乐部租一张球台开展活动，‎ 当15≤x≤30时，g(x)＝90；‎ 当30＜x≤40时，g(x)＝90＋2(x－30)＝2x＋30，‎ ‎∴g(x)＝‎ ‎(2)由f(x)＝g(x)，得或 5‎ 即x＝18或x＝10(舍去)．‎ 当15≤x＜18时，f(x)－g(x)＝5x－90＜0，‎ ‎∴f(x)＜g(x)，则此时选甲俱乐部；‎ 当x＝18时，f(x)＝g(x)，则此时可以选甲俱乐部也可以选乙俱乐部；‎ 当18＜x≤30时，f(x)－g(x)＝5x－90＞0，‎ ‎∴f(x)＞g(x)，则此时选乙俱乐部；‎ 当30＜x≤40时，f(x)－g(x)＝5x－(2x＋30)＝3x－30＞0，‎ ‎∴f(x)＞g(x)，则此时选乙俱乐部．‎ 综上所述：当15≤x＜18时，选甲俱乐部；‎ 当x＝18时，可以选甲俱乐部也可以选乙俱乐部；‎ 当18＜x≤40时，选乙俱乐部．‎ 5‎