山西省太原市2020届高三模拟试题（二）数学（理）试题

山西省太原市2020届高三模拟试题（二）数学（理）试题

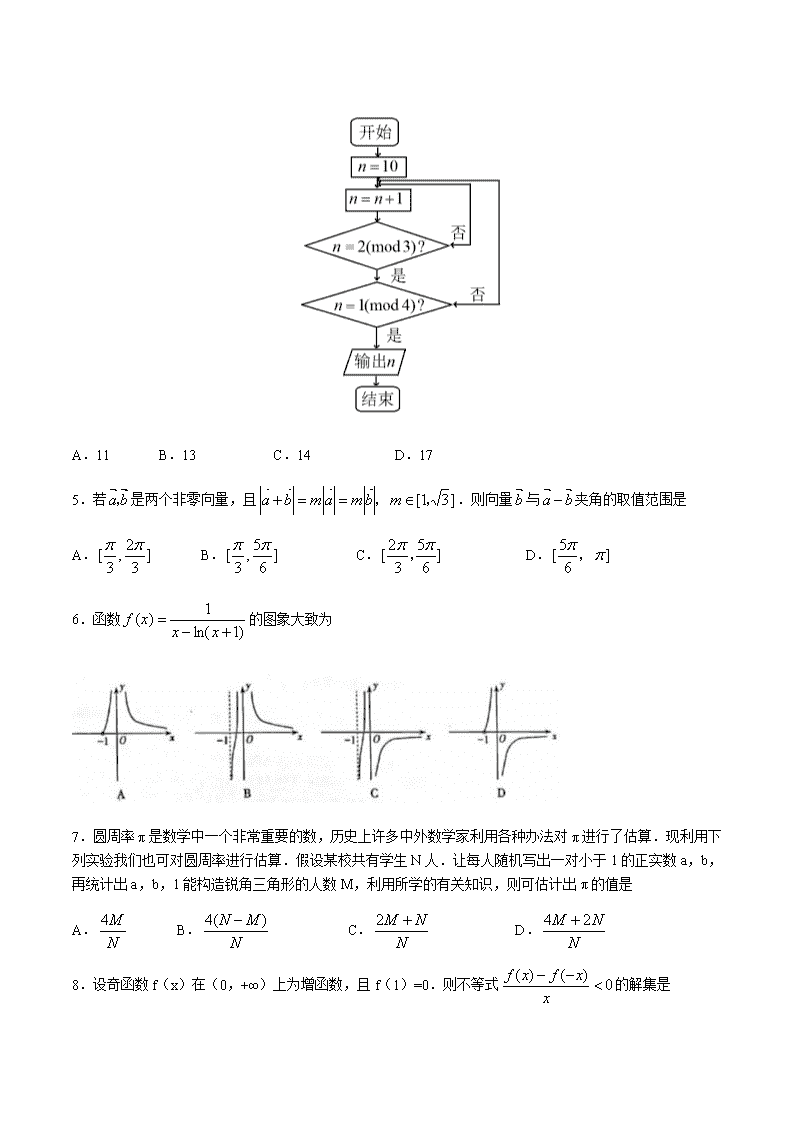
太原市2020年高三年级模拟试题（二）‎ 数学试卷（理科）‎ ‎（考试时间：下午3：00——5：00）‎ 注意事项：‎ ‎1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至4页，第Ⅱ卷5至8页。‎ ‎2．回答第Ⅰ卷前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎3．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，写在本试卷上无效。‎ ‎4．回答第Ⅱ卷时，将答案写在答题卡相应位置上，写在本试卷上无效。‎ ‎5．考试结束后，将本试卷和答题卡一并交回。‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中．只有一项是符合题目要求的．‎ ‎1．已知集合．则 A．A∩B={2} B．A∪B= R C． D．‎ ‎2．已知a是实数，是纯虚数，则a=‎ A．1 B．‎-1 C． D．‎ ‎3．已知，则 A．a＜b＜c B．a＜c＜b C．b＜a＜c D．c＜a＜b ‎4．右边程序框图的算法源于我国古代闻名中外的《中国剩余定理》．n≡N（modm）表示正整数n除以正整数m的余数为N，例如10≡ 4（ mod6）．执行该程序框图，则输出的n等于 A．11 B．‎13 C．14 D．17 ‎ ‎5．若是两个非零向量，且．则向量与夹角的取值范围是 A． B． C． D．‎ ‎6．函数的图象大致为 ‎7．圆周率π是数学中一个非常重要的数，历史上许多中外数学家利用各种办法对π进行了估算．现利用下列实验我们也可对圆周率进行估算．假设某校共有学生N人．让每人随机写出一对小于1的正实数a，b，再统计出a，b，1能构造锐角三角形的人数M，利用所学的有关知识，则可估计出π的值是 A． B． C． D．‎ ‎8．设奇函数f（x）在（0，+∞）上为增函数，且f（1）=0．则不等式的解集是 A．（-1，0）（1，+∞） B．（-1，0）（0，1）‎ C．（-∞，-1）（1，+∞） D．（-∞，-1）（0，1）‎ ‎9．过抛物线的焦点的直线与抛物线交于A，B两点，设点M（3，0）．若△MAB的面积为．则|AB|=‎ A．2 B．‎4 C． D．8‎ ‎10．已知数列的前n项和为．且满足．数列满足，则数列的前100项和为 A． B． C． D．‎ ‎11．对于函数．有下列说法：‎ ‎①f（x）的值城为[-1，1]；‎ ‎②当且仅当时，函数f（x）取得最大值；‎ ‎③函数f（x）的最小正周期是π； ‎ ‎④当且仅当时f（x）＞0．‎ 其中正确结论的个数是 A．1 B．‎2 C．3 D．4‎ ‎12．三棱锥P—ABC中．AB⊥BC，△PAC为等边三角形，二面角P—AC—B的余弦值为，当三棱锥的体积最大时，其外接球的表面积为8π ．则三棱锥体积的最大值为 A．1 B．‎2 C． D．‎ 第Ⅱ卷（非选择题共90分）‎ 本卷包括必考题和选考题两部分，第13题～第21题为必考题，每个试题考生都必须作答．第22题、第23题为选考题，考生根据要求作答．‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．已知的展开式中，x2的系数为0，则实数a = ．‎ ‎14．已知双曲线（a＞0，b＞0）的左右顶点分别为A，B，点P是双曲线上一点，若△PAB为等腰三角形，∠PAB= 120°，则双曲线的离心率为 ．‎ ‎15．已知数列{an}满足（n∈N*），且a2=6，则{an}的通项公式为 ．‎ ‎16．改革开放40年来，我国城市基础设施发生了巨大的变化，各种交通工具大大方便了人们的出行需求．某城市的A先生实行的是早九晚五的工作时间，上班通常乘坐公交或地铁加步行．已知从家到最近的公交站或地铁站都需步行5分钟，乘坐公交到离单位最近的公交站所需时间Z1（单位：分钟）服从正态分布N(33,42)，下车后步行再到单位需要12分钟；乘坐地铁到离单位最近的地铁站所需时间Z2（单位：分钟）服从正态分布N(44,22)，从地铁站步行到单位需要5分钟．现有下列说法：‎ ‎①若8：00出门，则乘坐公交一定不会迟到；‎ ‎②若8：02出门，则乘坐公交和地铁上班迟到的可能性相同；‎ ‎③若8：06出门，则乘坐公交比地铁上班迟到的可能性大；‎ ‎④若8：12出门，则乘坐地铁比公交上班迟到的可能性大．‎ 则以上说法中正确的序号是 ．‎ 参考数据：若Z~N(μ，σ2)，则P(μ－σ＜Z≤μ＋σ) = 0.6826， ‎ P(μ－2σ＜Z≤μ＋2σ) = 0.9544，‎ P(μ－3σ＜Z≤μ＋3σ) = 0.9974‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．‎ ‎（一）必考题：共60分．‎ ‎17．（本小题满分12分）‎ ‎△ABC的内角A，B，C的对边分别为a，b，c，若，且△ABC外接圆的半径为1．‎ ‎（Ⅰ）求角C；‎ ‎（Ⅱ）求△ABC面积的最大值．‎ ‎18．（本小题满分12分）‎ 如图，四边形ABCD是边长为4的菱形，∠BAD = 60°，对角线AC与BD相交于点O，四边形ACFE为梯形，EF//AC，点E在平面ABCD上的射影为OA的中点，AE与平面ABCD所成角为45°．‎ ‎（Ⅰ）求证：BD⊥平面ACF；‎ ‎（Ⅱ）求平面DEF与平面ABCD所成角的正弦值．‎ ‎19．（本小题满分12分）‎ 已知F1，F2是椭圆C：（a＞b＞0）的左、右焦点，过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为 ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）过F1的直线交椭圆于A，B两点，当△ABF2面积最大时，求直线的方程．‎ ‎20．（本小题满分12分）‎ 为实现2020年全面建设小康社会，某地进行产业的升级改造．经市场调研和科学研判，准备大规模生产某高科技产品的一个核心部件，目前只有甲、乙两种设备可以独立生产该部件．下图是从甲设备生产的部件中随机抽取400件，对其核心部件的尺寸x，进行统计整理的频率分布直方图．‎ 根据行业质量标准规定，该核心部件尺寸x满足：为一级品，为二级品，为三级品．‎ ‎（Ⅰ）现根据频率分布直方图中的分组，用分层抽样的方法先从这400件样本中抽取40件产品，再从所抽取的40件产品中，抽取2件尺寸x∈[ 12，15]的产品，记ξ为这2件产品中尺寸x∈[14，15 ]的产品个数，求ξ的分布列和数学期望；‎ ‎（Ⅱ）将甲设备生产的产品成箱包装出售时，需要进行检验．已知每箱有100件产品，每件产品的检验费用为50元．检验规定：若检验出三级品需更换为一级或二级品；若不检验，让三级品进入买家，厂家需向买家每件支付200元补偿．现从一箱产品中随机抽检了10件，结果发现有1件三级品．若将甲设备的样本频率作为总体的慨率，以厂家支付费用作为决策依据，问是否对该箱中剩余产品进行一一检验? 请说明理由；‎ ‎（Ⅲ）为加大升级力度，厂家需增购设备。已知这种产品的利润如下：一级品的利润为500元/件；二级品的利润为400元/件；三级品的利润为200元/件．乙种设备产品中一、二、三级品的概率分别是，，．若将甲设备的样本频率作为总体的概率，以厂家的利润作为决策依据．应选购哪种设备？请说明理由．‎ ‎21．（本小题满分12分） ‎ 已知函数．‎ ‎（Ⅰ）若函数f（x）有两个零点，求a的取值范围；‎ ‎（Ⅱ）恒成立，求a的取值范围．‎ ‎（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑．‎ ‎22．（本小题满分10分）[选修4—4：坐标系与参数方程]‎ 在平面直角坐标系xOy中，曲线C1的参数方程为（t为参数） ，曲线C2的参数方程为（为参数），以坐标原点为极点．x轴正半轴为极轴建立极坐标系．‎ ‎（Ⅰ）求曲线C1的普通方程和曲线C2的极坐标方程；‎ ‎（Ⅱ）射线与曲线C2交于O，P两点，射线与曲线C1交于点Q，若△OPQ的面积为1，求|OP|的值．‎ ‎23．（本小题满分10分）[选修4—5：不等式选讲]‎ 已知a，b，c为正实数．‎ ‎（Ⅰ）若a+b+c= 1，证明：；‎ ‎（Ⅱ）证明：‎