山西省平遥中学2018-2019学年高二下学期期中考试数学试卷（文）

山西省平遥中学2018-2019学年高二下学期期中考试数学试卷（文）

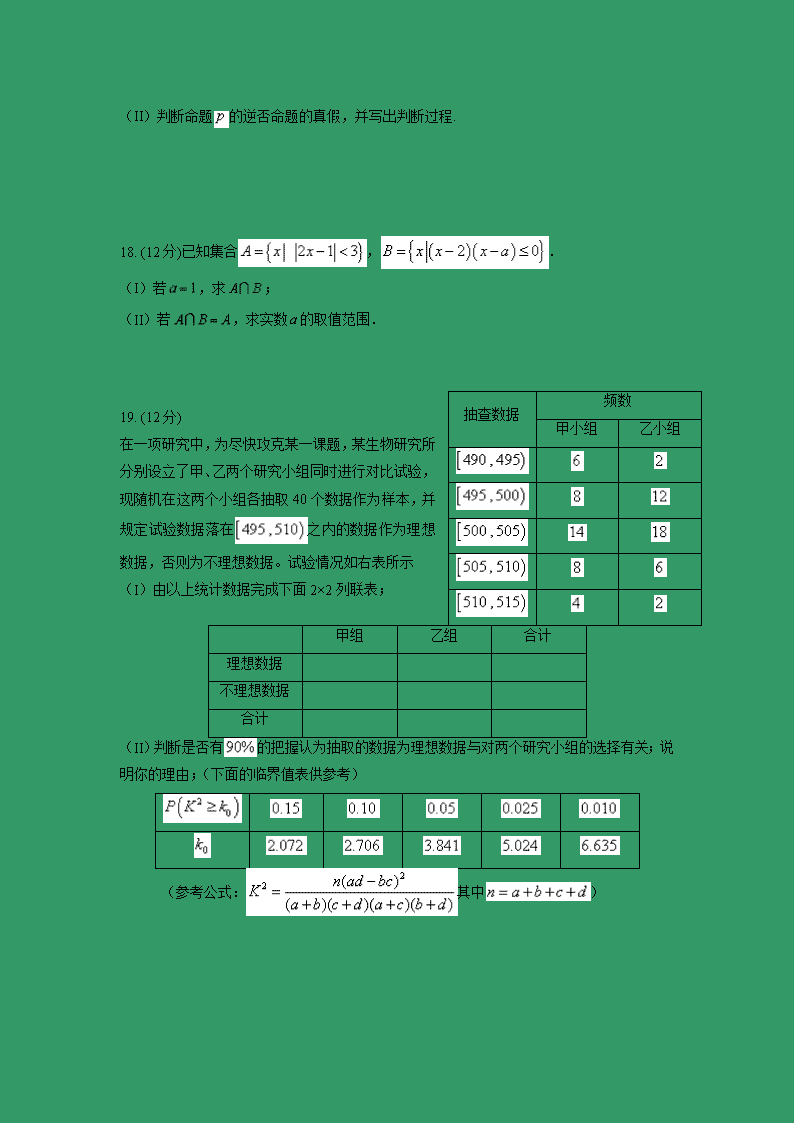
山西省平遥中学2018-2019学年高二下学期期中考试（文）‎ 一、选择题：本题共12小题，每小题5分，共60分 ‎1. 已知全集,集合,集合,则集合（ ）‎ A. B. C. D. ‎ ‎2. 设有一线性回归方程，变量每增加一个单位时，变量平均(　　)‎ A．增加6.5个单位 B．增加6个单位 C．减少6.5个单位 D．减少6个单位 ‎3. 已知命题 ，则其否定为（ ）‎ A． B．‎ C． D．‎ ‎4.“”是“复数(,)为纯虚数”的（ ）‎ A．必要不充分条件 B． 充分不必要条件 C．充要条件 D．既不充分也不必要条件 ‎5. 设集合，集合，则下列关系中正确的是（ ）‎ A. B. C. D. ‎ ‎6.如图所示，执行图中的程序框图，输出的值是（ ）‎ A．1 B．10 ‎ C．19 D．28‎ ‎7．由①正方形的四个内角相等；②矩形的四个内角相等；③正方形是矩形，根据“三段论”推理出一个结论，则作为大前提、小前提、结论的分别为(　　)‎ A．②③① B．③①② C．①②③ D．②①③‎ ‎8．设，是复数，则下列命题中的假命题是(　　)‎ A．若，则 B．若，则 C．若，则 D．若，则 ‎9．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．根据收集到的数据(如表)，由最小二乘 零件数x/个 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ 加工时间y/min ‎62‎ ‎75‎ ‎81‎ ‎89‎ 法求得回归方程为.现发现表中有一个数据模糊不清，经推断可知该数据为(　　)‎ A．70 B．68 C．66 D．64‎ ‎10．下列推理合理的是(　　)‎ A．若函数是增函数，则 B．因为(,)，则 (是虚数单位)‎ C．A是三角形ABC的内角，若，则此三角形为锐角三角形 D．,是锐角△ABC的两个内角，则 ‎11. 命题“”为真命题的一个充分不必要条件是（ ） (　　)‎ A． B． C． D．‎ ‎12. 若实数，满足，则的最大值是（ ）‎ ‎ A． B． C． D．‎ 二、填空题：本题共4小题，每小题5分，共20分 ‎13. 复数的共轭复数为 ‎ ‎14. 甲、乙、丙三名同学中只有一人考了满分，当他们被问到谁考了满分时，甲说：丙没有考满分；乙说：是我考的；丙说：甲说真话．事实证明：在这三名同学中，只有一人说的是假话，那么得满分的同学是 ‎ ‎15. 给出下列命题：‎ ‎①原命题为真，它的否命题为假； ②原命题为真，它的逆命题不一定为真； ‎ ‎③一个命题的逆命题为真，它的否命题一定为真； ④一个命题的逆否命题为真，它的否命题一定为真； ⑤“若，则的解集为”的逆命题，其中真命题是 (把你认为正确命题的序号都填在横线上)‎ ‎16. 如图，第个图形是由正边形“扩展”而来，则第个图形中共有 个顶点．‎ 三、解答题：共70分 ‎17. (10分)设命题：“若，则有实根”. ‎ ‎（I）试写出命题的逆否命题；‎ ‎（II）判断命题的逆否命题的真假，并写出判断过程.‎ ‎18. (12分)已知集合，．‎ ‎（I）若，求；‎ 抽查数据 频数 甲小组 乙小组 ‎（II）若，求实数的取值范围．‎ ‎19. (12分)‎ 在一项研究中，为尽快攻克某一课题，某生物研究所分别设立了甲、乙两个研究小组同时进行对比试验，现随机在这两个小组各抽取40个数据作为样本，并规定试验数据落在之内的数据作为理想数据，否则为不理想数据。试验情况如右表所示 ‎（I）由以上统计数据完成下面2×2列联表；‎ 甲组 乙组 合计 理想数据 不理想数据 合计 ‎（II）判断是否有的把握认为抽取的数据为理想数据与对两个研究小组的选择有关；说明你的理由；（下面的临界值表供参考）‎ ‎（参考公式：其中）‎ ‎20. (12分)已知极坐标系的极点为直角坐标系的原点，极轴为轴的正半轴，两种坐标系中的长度单位相同，已知曲线的极坐标方程为．‎ ‎（Ⅰ）求曲线的直角坐标方程；‎ ‎（Ⅱ）经过点直线（为参数）与曲线交于，两点，‎ 求的值．‎ ‎21. （12分）已知函数（）.‎ ‎（I）若，解不等式；‎ ‎（II）对任意，恒成立，求实数的取值范围. ‎ ‎22. （12分）某电视厂家准备在五一举行促销活动，现在根据近七年的广告费与销售量的 数据确定此次广告费支出.广告费支出（万元）和销售量（万台）的数据如下：‎ 年份 ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎2018‎ 广告费支出 销售量 ‎（I）若用线性回归模型拟合与的关系，求出关于的线性回归方程 ‎（其中；参考方程：回归直线，）‎ ‎（II）若用模型拟合与的关系，可得回归方程，经计算线性回归模型和该模型的分别约为和，请用说明选择哪个回归模型更好；‎ ‎（III）已知利润与，的关系为.根据（II）的结果回答：当广告费时，销售量及利润的预报值是多少？（精确到）参考数据：‎ 参考答案 ‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ B C D A B C A C B D C A ‎13. 14. 甲 15. ②③⑤ 16. ‎ ‎17. （I）逆否命题:若无实根，则；……………5分 ‎（II）因为无实根，所以，所以，‎ 所以“若无实根，则”为真命题. ………………10分 ‎18. 由题意知， ‎ ‎（I）当时，，从而 ………………5分 ‎（II）由得；①当时，，不合题意；‎ ②当时，，由得；‎ ③当时，，此时，不合题意；‎ 综上所述，实数的取值范围是. ………………12分 甲组 乙组 合计 理想数据 ‎30‎ ‎36‎ ‎66‎ 不理想数据 ‎10‎ ‎4‎ ‎14‎ 合计 ‎40‎ ‎40‎ ‎80‎ ‎19. （I）‎ ‎……6分 ‎（II）由表中数据得的观测值为 故有的把握认为抽取的数据为理想数据与对两个研究小组的选择有关. ……12分 ‎20.（I） …………5分 ‎（II）将的参数方程代入曲线的直角坐标方程，得，‎ 设点，对应的参数分别为，，则， ‎ 则. ………12分 ‎21. （I）若，‎ ① 当时，解得；‎ ② 当时，解得 ③ 当时，解得 综上所述，不等式的解集为 ………6分 ‎（II），‎ 若对任意，恒成立，只需，解得.‎ 所以实数的取值范围是. ………12分 ‎22.（I）由题意有，，，‎ ‎，‎ 所以关于的线性回归方程为； ………6分 ‎（II）越接近于1，模型的拟合效果越好，故选用 ……8分 ‎（III）广告费时，销售量预报值（万台），‎ 利润的预报值（万元） ……12分