2020届二轮复习函数的(实际)应用课件（全国通用）

2020届二轮复习函数的(实际)应用课件（全国通用）

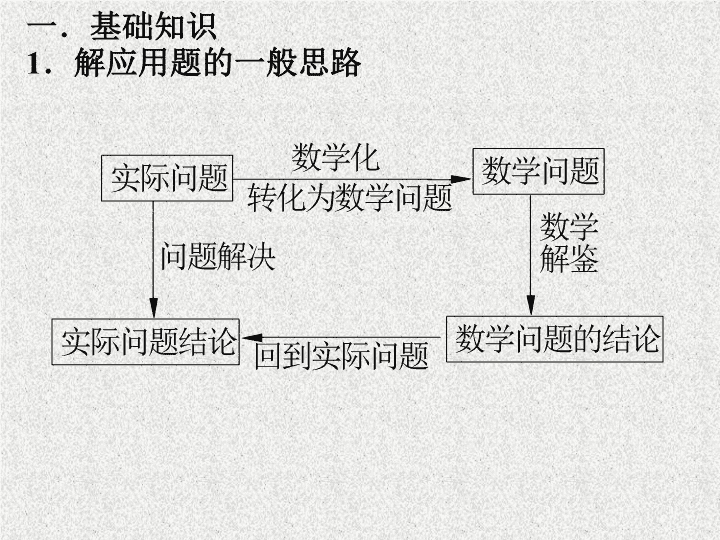
函数的实际应用 高三备课组 一．基础知识 1．解应用题的一般思路 2. 解应用题的一般程序 (1)审题：阅读理解文字表达的题意,分清条件和结论,理顺数量关系,这一关是基础. (2)建模：将文字语言转化为数学语言,利用数学知识,建立相应的数学模型,正确进行建“模”是关键的一关。 (3)求模：求解数学模型，得到数学结论，要充分注重数学模型中元素的实际意义，更要注意巧思妙作，优化过程。 (4)作答：将数学结论还原给实际问题的过程。 3 ．常见函数模型 (1)应用 的模型解决有关增长率及利息等问题。 (2)分段函数模型。 (3)应用二次函数模型解决有关最值问题。 (4)数列模型。 例2 ． 某农产品去年各季度的市场价格如下表： 今年某公司计划按去年各季度市场价的“最佳近似值 m”（m 是与上表中各售价差的平方和取最小值时的值）收购该种农产品，并按每100元纳税10元（又称征税率为10个百分点），计划可收购 a 万担，政府为了鼓励收购公司多收购这种农产品，决定将税率降低 x 个百分点，预测收购量可增加2 x 个百分点。 （1）根据题中条件填空， m= （ 元/担） （2）写出税收 y（ 万元）与 x 的函数关系式； （3）若要使此项税收在税率调节后不少于原计划税收的83.2%，试确定 x 的取值范围。 例1：书 P29 例1 练习： 某校办工厂有毁坏的房屋一幢，留有旧墙一面，其长14 m, 现准备利用这面旧墙，建造平面图形为矩形，面积为126 cm 2 的厂房，工程条件：（1）修1 m 旧墙的费用是建1 m 新墙的费用的25%，（2）用拆去1 m 旧墙的材料建1 m 新墙，其费用是建1 m 新墙费用的50%，（3）建门窗的费用与建新墙的费用相同，问：如何利用旧墙才能使建墙费用最低？ 例3：书 P30 例2 例4：书 P30 例3 练习：东方旅社有100张普通客床，每床每夜收租费10元时，客床可以全部租出，若每床每夜收费提高2元，便减少10张床租出，再提高2元，又再减少10张床租出，依此变化下去，为了投资少而获利大，每床每夜应提高租金（ ） A．4 元 B、6 元 C、4 元或6元 D、8 元 例5：书 P30 例4 三．小结 1．解应用题的一般步骤：审题、建模、求模、作答 2．常见函数模型 （1）增长率模型（如例1，例2） （2）分段函数模型（如例3） （3）二次函数（如例4） （4）数列模型（如例5） 四、作业： 优化设计