【数学】2018届一轮复习人教A版第05讲分离参数法-高中数学常用的解题技巧学案

【数学】2018届一轮复习人教A版第05讲分离参数法-高中数学常用的解题技巧学案

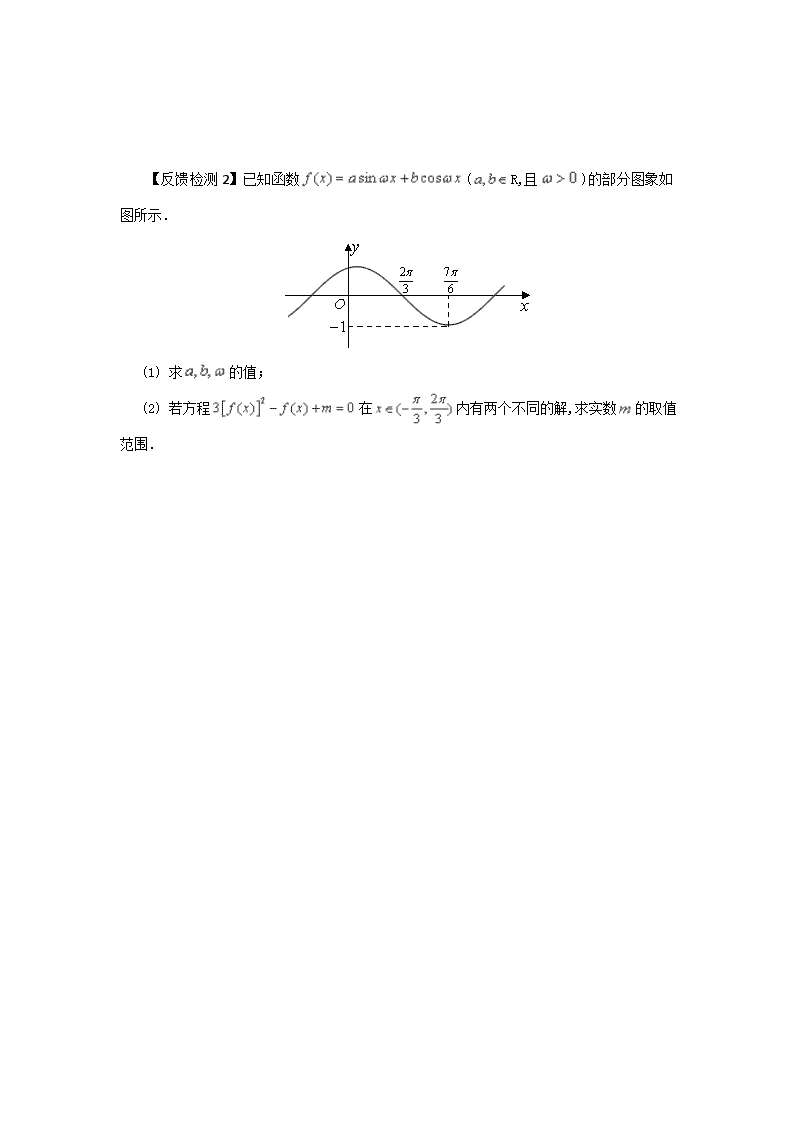
‎ 高中数学常用解题技巧第05讲：分离参数法 ‎【知识要点】‎ ‎ 一、参数在数学问题中经常出现，特别是在最值、值域、取值范围、恒成立和存在性等问题中，经常出现，这时可以考虑是否可以利用分离参数法 解答，即整理成的形式，再解答.‎ 二、分离参数时，一定要判断清楚参数的系数的符号，再除以其系数，如果不能确定其符号，可以分类讨论，也可以寻找其它方法.‎ ‎【方法讲评】‎ ‎【例1】已知函数 ‎（1）求曲线在点处的切线方程；‎ ‎（2）求函数的极值；‎ ‎（3）对恒成立，求实数的取值范围．‎ ‎ ‎ 列表：‎ ‎-‎ ‎0‎ ‎+‎ ‎↘‎ ‎↗‎ 函数的极小值为, 无极大值。 ‎ ‎（3）依题意对恒成立等价于在上恒成立 可得在上恒成立， ‎ 令 ‎ ‎【点评】本题第（2）问是恒成立问题，刚好的系数是一个正数，知道参数的系数的符号，分离参数很方便，所以可以分离参数求最值,比较简洁.‎ ‎【反馈检测1】已知函数. （1）若,试判断在定义域内的单调性；‎ ‎（2）若在上的最小值为,求的值；‎ ‎（3）若在上恒成立,求的取值范围.‎ ‎ ‎ ‎【反馈检测2】已知函数(R,且)的部分图象如图所示．‎ ‎(1) 求的值；‎ ‎(2) 若方程在内有两个不同的解,求实数的取值范围．‎ 高中数学常用解题技巧第05讲：分离参数法参考答案 ‎【反馈检测1答案】(1) 在上是单调递增函数；（2） ；（3）.‎ ‎【反馈检测1详细解析】（1）由题意知的定义域为,且,‎ ‎∴, 故在上是单调递增函数 ‎ ‎（2）由（1）可知, . 当时, ∴在上为减函数; 当时, ,∴在上为增函数, ∴.综上所述, ‎ ‎（3）∵.又， 令. ∵时, 在上是减函数.x.kw ∴,即在上也是减函数. ,∴当时, 在上恒成立. ‎ ‎【反馈检测2答案】（1），；（2）或.‎ ‎【反馈检测2详细解析】(1) ‎ 由图像可知函数周期为，得 ‎ 解得 ‎