- 2021-06-10 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020高考数学二轮复习练习:第一部分 小题强化练 小题强化练(八)含解析
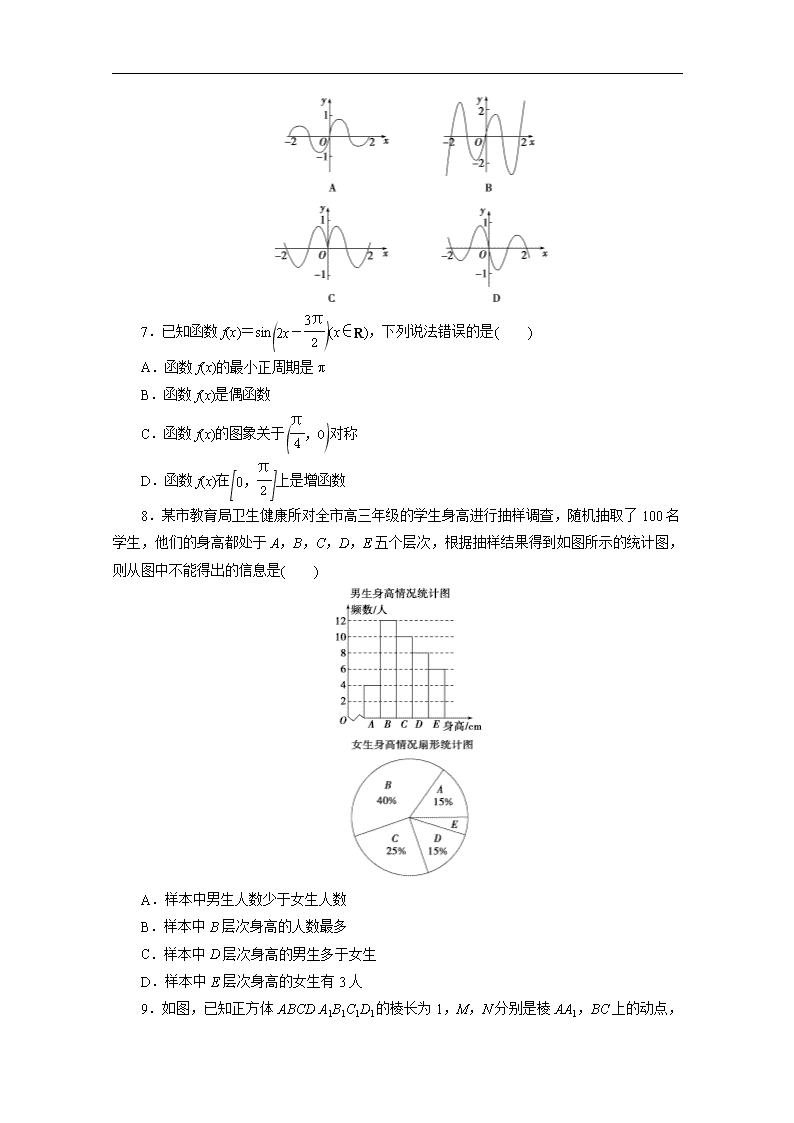
小题强化练(八) 一、选择题 1.已知集合M={1,a2},P={-1,-a},若M∪P有三个元素,则M∩P=( ) A.{0,1} B.{-1,0} C.{0} D.{-1} 2.若复数z=,且z·i3>0,则实数a的值等于( ) A.1 B.-1 C. D.- 3.已知条件甲:a>0,条件乙:a>b且>,则甲是乙的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 4.已知数列{an}满足3an+1=9·3an(n∈N*)且a2+a4+a6=9,则log(a1+a9+a11)=( ) A.- B.3 C.-3 D. 5.已知非零向量a,b满足|a+b|=|a-b|=2,|a|=1,则a+b与a-b的夹角为( ) A. B. C. D. 6.函数f(x)=sin(πx)e-的图象可能是( ) 7.已知函数f(x)=sin(x∈R),下列说法错误的是( ) A.函数f(x)的最小正周期是π B.函数f(x)是偶函数 C.函数f(x)的图象关于对称 D.函数f(x)在上是增函数 8.某市教育局卫生健康所对全市高三年级的学生身高进行抽样调查,随机抽取了100名学生,他们的身高都处于A,B,C,D,E五个层次,根据抽样结果得到如图所示的统计图,则从图中不能得出的信息是( ) A.样本中男生人数少于女生人数 B.样本中B层次身高的人数最多 C.样本中D层次身高的男生多于女生 D.样本中E层次身高的女生有3人 9.如图,已知正方体ABCDA1B1C1D1的棱长为1,M,N分别是棱AA1,BC上的动点,若MN=,则线段MN的中点P的轨迹是( ) A.一条线段 B.一段圆弧 C.一个球面区域 D.两条平行线段 10.已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,O为坐标原点,以线段F1F2为直径的圆与双曲线的右支交于P点,且以线段OF2为直径的圆与直线PF1相切,若|PF1|=8,则双曲线的焦距等于( ) A.6 B.6 C.3 D.3 11.(多选)在△ABC中,内角A,B,C的对边分别为a,b,c,则( ) A.若2cos C(acos B+bcos A)=c,则角C= B.若2cos C(acos B+bcos A)=c,则角C= C.若边BC上的高为a,则当+取得最大值时,角A= D.若边BC上的高为a,则当+取得最大值时,角A= 12.(多选)如图,正方体ABCDA1B1C1D1的棱长为3,线段B1D1上有两个动点E,F且EF=1,则当E,F移动时,下列结论正确的是( ) A.AE∥平面C1BD B.四面体ACEF的体积不为定值 C.三棱锥ABEF的体积为定值 D.四面体ACDF的体积为定值 13.(多选)某同学在研究函数f(x)=(x∈R)时,分别得出下面几个结论,其中正确的结论是( ) A.等式f(-x)+f(x)=0在x∈R时恒成立 B.函数f(x)的值域为(-1,1) C.若x1≠x2,则一定有f(x1)≠f(x2) D.函数g(x)=f(x)-x在R上有三个零点 二、填空题 14.设a∈{1,3,5,7},b∈{2,4,6},则函数f(x)=logx 是增函数的概率为________. 15.已知正实数a,b满足ab-b+1=0,则+4b的最小值是________. 16.已知数列{an}的首项a1=1,函数f(x)=x3+为奇函数,记Sn为数列{an}的前n项和,则S2 019的值为________. 17.已知椭圆C:+=1(a>b>0)的两个焦点分别为F1,F2,若B为短轴的一个端点,且∠F1BF2=90°,则椭圆C的离心率为________;若椭圆C上存在点P,使得PF1⊥PF2,则椭圆C的离心率的取值范围为________. 小题强化练(八) 1.解析:选C.要使M∪P有三个元素,则a2=-a,即a=0或a=-1,若a=-1,则有a2=1不合题意,所以a=0,则M∩P={0}. 2.解析:选A.z·i3=z·(-i)===,因为z·i3>0,所以z·i3为正实数,则有所以a=1. 3.解析:选B.若>,则>0.又a>b,所以ab<0,即a>0>b,故甲是乙的必要不充分条件. 4.解析:选C.由题意得3an+1=3an+2即,an+1-an=2,所以{an}是公差为2的等差数列.由a2+a4+a6=3a4=9得a4=3,所以an=3+(n-4)×2=2n-5,所以log(a1+a9+a11)=log(-3+13+17)=log27=-3. 5.解析:选C.法一:由|a+b|=|a-b|=2可得a·b=0,则有|a+b|2=|a|2+|b|2=4,所以|b|2=4-|a|2=3. 因为|a-b|=2,所以cos〈a+b,a-b〉===-.因为〈a+b,a-b〉∈[0,π],所以〈a+b,a-b〉=. 法二:由题设|a+b|=|a-b|=2及向量的加减运算的几何意义可知以a,b为邻边的平行四边形是矩形,即a⊥b,如图.由于|a+b|=|a-b|=2,|a|=1,则OA=OC=AC=1,则∠ACO=,则向量a+b与a-b的夹角∠ACD=. 6.解析:选A.因为f(-x)=sin(-πx)e-=-sin(πx)e-=-f(x),所以f(x)为奇函数,故排除C;令0查看更多