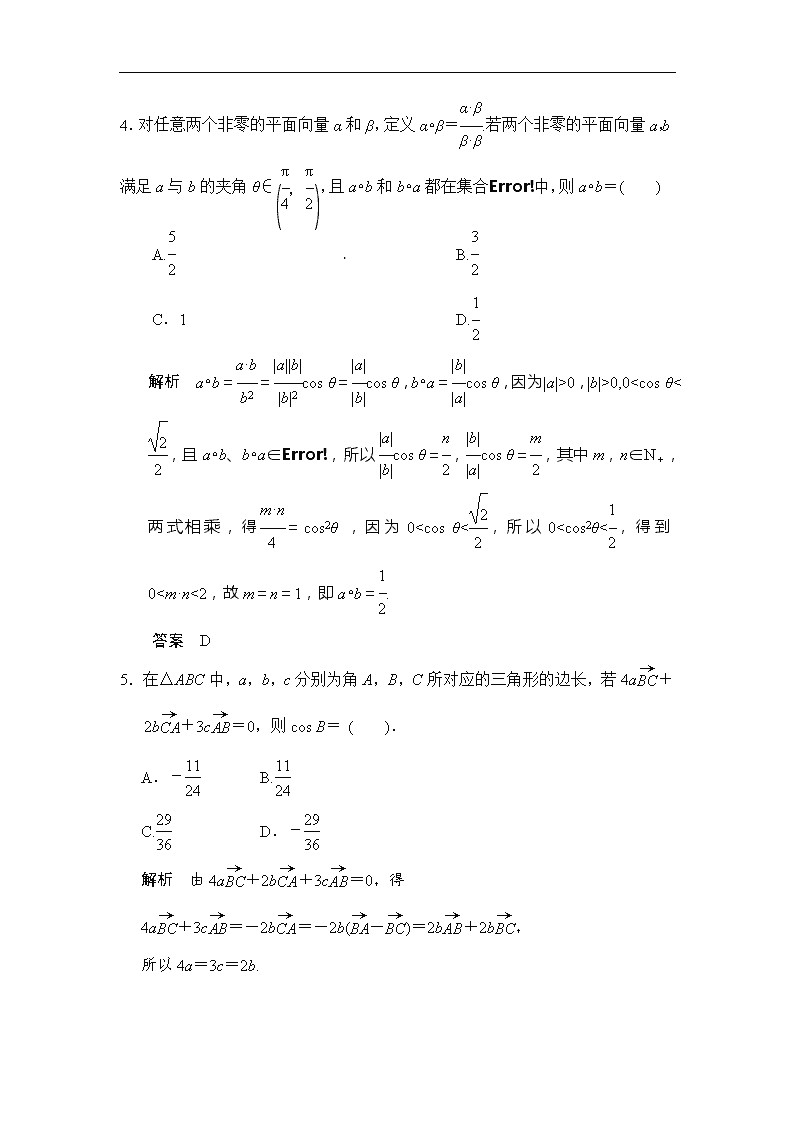高考数学复习专题练习第4讲 平面向量应用举例
第4讲 平面向量应用举例
一、选择题
1.已知锐角三角形ABC中,||=4,||=1,△ABC的面积为,则·的值为( )
A.2 B.-2
C.4 D.-4
解析 由题意得×||×||×sin A=,所以×4×1×sin A=,故sin A=,又A为锐角,所以A=60°,·=||×||×cos A=4×1×cos 60°=2.
答案 A
2.若|a|=2sin 15°,|b|=4cos 15°,a与b的夹角为30°,则a·b的值是 ( ).
A. B. C.2 D.
解析 a·b=|a||b|cos 30°=8sin 15°cos 15°×=4×sin 30°×=.
答案 B
3. 函数y=tanx-的部分图象如图所示,
则(+)·=( ).
A.4 B.6
C.1 D.2
解析 由条件可得B(3,1),A(2,0),
∴(+)·=(+)·(-)=2-2=10-4=6.
答案 B
4.对任意两个非零的平面向量α和β,定义α∘β=.若两个非零的平面向量a,b
满足a与b的夹角θ∈,且a∘b和b∘a都在集合中,则a∘b=( )
A. B.[来源:Z#xx#k.Com]
C.1 D.
解析 a∘b==cos θ=cos θ,b∘a=cos θ,因为|a|>0,|b|>0,0
0,即4|b|2-8|b|2cos〈a,b〉>0,即-1≤cos〈a,b〉<.所以a与b的夹角范围为.
答案
三、解答题
11.已知△ABC的角A、B、C所对的边分别是a、b、c,设向量m=(a,b),n=(sin B,sin A),p=(b-2,a-2).
(1)若m∥n,求证:△ABC为等腰三角形;
(2)若m⊥p边长c=2,角C=,求△ABC的面积.
解 (1)证明:∵m∥n,∴asin A=bsin B,
即a·=b·,其中R是三角形ABC外接圆半径,
∴a=b.∴△ABC为等腰三角形.
(2)由题意可知m·p=0,即a(b-2)+b(a-2)=0.
∴a+b=ab.
由余弦定理可知,4=a2+b2-ab=(a+b)2-3ab,
即(ab)2-3ab-4=0,∴ab=4(舍去ab=-1),
∴S=absin C=×4×sin=.
12.已知A,B,C的坐标分别为A(3,0),B(0,3),C(cos α,sin α),α∈.
(1)若||=||,求角α的值;
(2)若·=-1,求的值.
解 (1)∵=(cos α-3,sin α),=(cos α,sin α-3),
∴2=(cos α-3)2+sin2α=10-6cos α,
2=cos2α+(sin α-3)2=10-6sin α,
由||=||,可得2=2,
即10-6cos α=10-6sin α,得sin α=cos α.
又α∈,∴α=.
(2)由·=-1,
得(cos α-3)cos α+sin α(sin α-3)=-1,
∴sin α+cos α=.①
又==2sin αcos α.
由①式两边分别平方,得1+2sin αcos α=,
∴2sin αcos α=-.
∴=-.
13.在△ABC中,内角A,B,C的对边分别为a,b,c,向量m=(2sin B,-),n=且m∥n.
(1)求锐角B的大小;
(2)如果b=2,求S△ABC的最大值.
解 (1)∵m∥n,∴2sin B=-cos 2B,
∴sin 2B=-cos 2B,即tan 2B=-.
又B为锐角,∴2B∈(0,π),∴2B=,∴B=.
(2)∵B=,b=2,由余弦定理cos B=,
得a2+c2-ac-4=0.又a2+c2≥2ac,代入上式,
得ac≤4(当且仅当a=c=2时等号成立).
S△ABC=acsin B=ac≤(当且仅当a=c=2时等号成立),即S△ABC的最大值为.
14.已知向量m=,
n=.
(1)若m·n=1,求cos的值;
(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
解 (1)m·n=sin ·cos +cos2
=sin +=sin+,
∵m·n=1,∴sin=.
cos=1-2sin2=,
cos=-cos=-.
(2)∵(2a-c)cos B=bcos C,
由正弦定理得(2sin A-sin C)cos B=sin Bcos C,
∴2sin Acos B-sin Ccos B=sin Bcos C.
∴2sin Acos B=sin(B+C).
∵A+B+C=π,∴sin(B+C)=sin A≠0.
∴cos B=,∵0<B<π,∴B=,∴0<A<.
∴<+<,sin∈.
又∵f(x)=sin+,∴f(A)=sin+.
故函数f(A)的取值范围是.