高考数学人教A版（理）一轮复习：易失分点清零(十) 立体几何(二)

高考数学人教A版（理）一轮复习：易失分点清零(十) 立体几何(二)

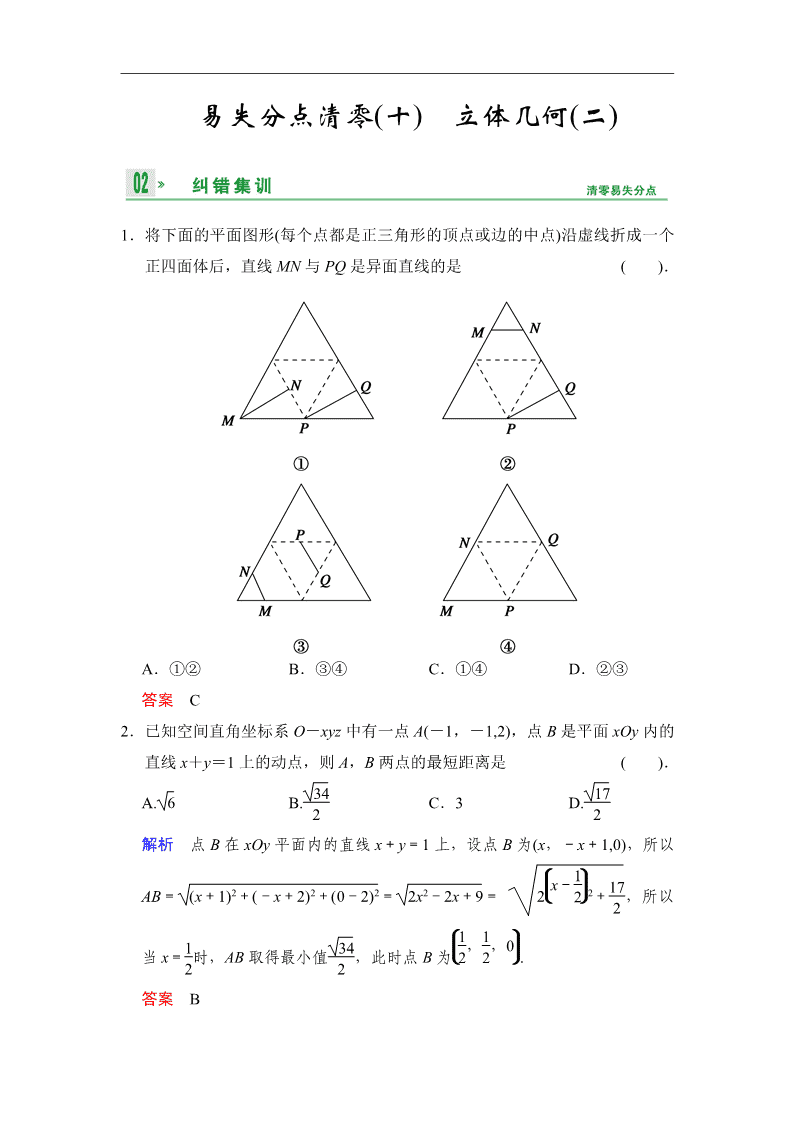
易失分点清零(十)　立体几何(二)‎ ‎1．将下面的平面图形(每个点都是正三角形的顶点或边的中点)沿虚线折成一个正四面体后，直线MN与PQ是异面直线的是 (　　)．[来源:学科网ZXXK]‎ ‎[来源:学科网]‎ A．①② B．③④ C．①④ D．②③‎ 答案　C ‎2．已知空间直角坐标系O－xyz中有一点A(－1，－1,2)，点B是平面xOy内的直线x＋y＝1上的动点，则A，B两点的最短距离是 (　　)．‎ A. B. C．3 D. 解析　点B在xOy平面内的直线x＋y＝1上，设点B为(x，－x＋1,0)，所以AB＝＝＝ ，所以当x＝时，AB取得最小值，此时点B为.‎ 答案　B ‎3．空间四边形OABC中，OB＝OC，∠AOB＝∠AOC＝，则cos〈，〉的值为 (　　)．‎ A. B. C．－ D．0‎ 解析　因为·＝·(－)＝·－·＝||·||cos 〈，〉－||||cos〈，〉又因为〈，〉＝〈，〉＝，||＝||，所以·＝0，所以⊥，所以cos 〈，〉＝0.‎ 答案　D ‎4．已知a，b是异面直线，A、B∈a，C、D∈b，AC⊥b，BD⊥b，且AB＝2，CD＝1，则a与b所成的角是 (　　)．‎ A．30° B．45° C．60° D．90°‎ 解析　因为·＝(＋＋)·＝2＝1.‎ 所以cos〈，〉＝＝.‎ 所以AB与CD所成的角为60°，即异面直线a与b所成的角为60°.‎ 答案　C ‎5．在长方体ABCD－A1B1C1D1中，AB＝2，BC＝1，DD1＝3，则AC与BD1所成角的余弦值是 (　　)．‎ A．0 B. ‎ C．－ D.[来源:学科网]‎ 解析　分别以直线DA，DC，DD1为x轴，y轴，z 轴建立空间直角坐标系，则A(1,0,0)，B(1,2,0)，C(0,2,0)，D1(0,0,3)，＝(－1,2,0)，1＝(－1，－2,3)，[来源:Zxxk.Com]‎ cos〈，〉＝ ‎＝ ‎＝－，故AC与BD1所成角的余弦值为.‎ 答案　B ‎6．如果平面的一条斜线和它在这个平面上的射影的方向向量分别是a＝(1,0,1)，b＝(0,1,1)，那么这条斜线与平面所成的角是 (　　)．‎ A．90° B．60° C．45° D．30°‎ 解析　∵cos〈a，b〉＝＝，又∵〈a，b〉∈[0，π]，‎ ‎∴〈a，b〉＝60°.‎ 答案　B ‎7.二面角α－l－β为60°，A，B是棱l上的两点，AC，BD分别在半平面α，β内，AC⊥l，BD⊥l，且AB＝AC＝a，BD＝2a，则CD的长为 (　　)．‎ A．2a 　　　　 B.a [来源:学,科,网Z,X,X,K]‎ C．a 　　　　 D.a 解析　∵AC⊥l，BD⊥l，∴〈，〉＝60°，且·＝0，·＝0，‎ ‎∴＝＋＋，∴||＝ ‎＝＝2a.‎ 答案　A ‎8．在矩形ABCD中，AB＝1，BC＝，PA⊥平面ABCD，PA＝1，则PC与平面ABCD所成角是 (　　)．‎ A．30° B．45° C．60° D．90°‎ 解析　建立如图所示的空间直角坐标系，则P(0，0,1)，C(1，，0)，＝(1，，－1)，平面ABCD的一个法向量为n＝(0,0,1)，所以cos〈，n〉＝＝－，所以〈，n〉＝120°，所以斜线PC与平面ABCD的法向量所在直线所成角为60°，所以斜线PC与平面ABCD所成角为30°.‎ 答案　A ‎9．已知平面α的一个法向量n＝(－2，－2,1)，点A(－1,3,0)在α内，则点P(－2,1,4)到平面α的距离为 (　　)．‎ A．10 B．3 C. D. 解析　＝(1,2，－4)，∴P到平面α的距离d＝＝＝＝.‎ 答案　D ‎10.如图所示，已知点P为菱形ABCD外一点，且PA⊥面ABCD，PA＝AD＝AC，点F为PC中点，则二面角C－BF－D的正切值为 (　　)．‎ A. B. C. D. 解析　如图所示，连接AC，AC∩BD＝O，连接OF.以O为原点，OB、OC、OF所在直线分别为x，y，z轴建立空间直角坐标系O－xyz.设PA＝AD＝AC＝1，则BD＝.所以B，‎ F，C0，，0，D.‎ 结合图形可知，＝且为面BOF的一个法向量，由＝，＝，‎ 可求得面BCF的一个法向量n＝(1，，)．‎ 所以cos〈n，〉＝，sin〈n，〉＝，‎ 所以tan〈n，〉＝.‎ 答案　D ‎11．(2013·兰州模拟)已知点A(λ＋1，μ－1,3)，B(2λ，μ，λ－2μ)，C(λ＋3，μ－3,9)三点共线，则实数λ＋μ＝________.‎ 解析　因为＝(λ－1,1，λ－2μ－3)，＝(2，－2,6)，若A，B，C三点共线，则∥，即＝－＝，解得λ＝0，μ＝0，所以λ＋μ＝0.‎ 答案　0‎ ‎12．已知A(2,5，－6)，在xOy平面上存在点B，使得||＝3，则点B到原点的最短距离为________．‎ 解析　设B(x，y,0)，由||＝＝3，得(x－2)2＋(y－5)2‎ ‎＝9，所以点B在xOy平面内以C(2,5)为圆心，以3为半径的圆上，到原点的最短距离是|OC|－3＝－3.‎ 答案　－3‎ ‎13．(2013·泰安模拟)如图，正方形ACDE与等腰直角三角形ACB所在的平面互相垂直，且AC＝BC＝2，∠ACB＝90°，F、G分别是线段AE、BC的中点．AD与GF所成角的余弦值为________．‎ 解析　以C为原点建立空间直角坐标系C－xyz，A(0,2,0)，B(2,0,0)，D(0,0,2)，G(1,0,0)，F(0,2,1)，＝(0，－2,2)，＝(－1,2，1)，||＝2，||＝，·＝－2，cos〈，〉＝＝－.‎ 故AD与GF所成角的余弦值为.‎ 答案　 ‎14．如图，四棱锥P－ABCD中，底面ABCD是矩形，PD⊥平面ABCD，且PD＝AD＝1，AB＝2，点E是AB上一点．AE等于________时二面角P－EC－D的平面角为.‎ 解析　以D为原点，射线DA，DC，DP为x，y，z轴的正方向，建立空间直角坐标系，则P(0,0,1)，C(0,2,0)，＝(0,2，－1)．‎ 设E(1，y0,0)，则＝(－1，2－y0,0)，设平面PEC的法向量为n1＝(x，y，z)，‎ ‎∴⇒ 令y＝1，得n1＝(2－y0,1,2)，‎ 而平面ECD的法向量n2＝(0,0,1)，‎ 设二面角P－EC－D的平面角为θ，‎ ‎∴cos θ＝＝＝⇒y0＝2－，即AE＝2－.‎ 答案　2－ ‎15．已知三棱锥P－ABC中，PA⊥平面ABC，AB⊥AC，PA＝AC＝AB，N为AB上一点，AB＝4AN，M，S分别为PB，BC的中点．‎ ‎(1)证明：CM⊥SN；‎ ‎(2)求SN与平面CMN所成角的大小．‎ ‎(1)证明　设PA＝1，以A为原点，AB，AC，AP所在直线为x，y，z轴正方向建立空间直角坐标系如图所示．则P(0,0,1)，C(0,1,0)，B(2,0,0)，M，N，S，‎ 所以＝，＝.‎ 因为·＝－＋＋0＝0，所以CM⊥SN.‎ ‎(2)＝，设a＝(x，y，z)为平面CMN的一个法向量．则即令x＝2，得a＝(2,1，－2)．因为|cos〈a，〉|＝＝.‎ 所以SN与平面CMN所成角为45°.‎