- 2021-06-10 发布 |
- 37.5 KB |
- 5页


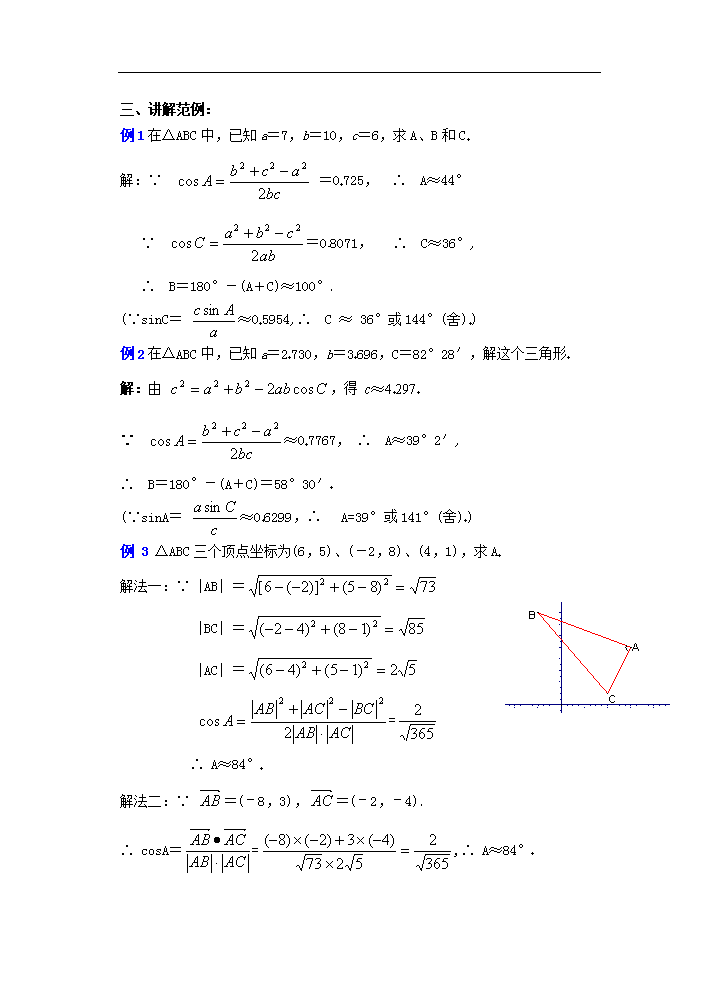
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修1教案:第五章(第14课时)正弦定理、余弦定理(2)
课 题:正弦定理、余弦定理(2) 教学目的: 1.掌握正弦定理、余弦定理; 2.使学生能初步运用它们解斜三角形,并会解决斜三角形的计算问题 教学重点:正弦定理、余弦定理的运用 教学难点:正弦定理、余弦定理的灵活运用 授课类型:新授课 课时安排:1课时 教 具:多媒体、实物投影仪 教学过程: 一、复习引入: 1正弦定理:在任一个三角形中,各边和它所对角的正弦比相等, 即 == =2R(R为△ABC外接圆半径) 2正弦定理的应用 从理论上正弦定理可解决两类问题: 1.两角和任意一边,求其它两边和一角; 2.两边和其中一边对角,求另一边的对角,进而可求其它的边和角(见图示)已知a, b和A, 用正弦定理求B时的各种情况: ⑴若A为锐角时: ⑵若A为直角或钝角时: 3.在Rt△ABC中(若C=90°)有: 在斜三角形中一边的平方与其余两边平方和及其夹角还有什么关系呢? 二、讲解新课: 1.余弦定理 :三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍 即 [问题] 对于任意一个三角形来说,是否可以根据一个角和夹此角的两边,求出此角的对边? [推导] 如图在中,、、的长分别为、、 ∵ ∴ 即 同理可证 , 2.余弦定理可以解决的问题 利用余弦定理,可以解决以下两类有关三角形的问题: (1)已知三边,求三个角; (2)已知两边和它们的夹角,求第三边和其他两个角 三、讲解范例: 例1在ΔABC中,已知a=7,b=10,c=6,求A、B和C 解:∵ =0725, ∴ A≈44° ∵ =08071, ∴ C≈36°, ∴ B=180°-(A+C)≈100° (∵sinC= ≈05954,∴ C ≈ 36°或144°(舍)) 例2在ΔABC中,已知a=2730,b=3696,C=82°28′,解这个三角形 解:由 ,得 c≈4297 ∵ ≈07767, ∴ A≈39°2′, ∴ B=180°-(A+C)=58°30′ (∵sinA= ≈06299,∴ A=39°或141°(舍)) 例 3 ΔABC三个顶点坐标为(6,5)、(-2,8)、(4,1),求A 解法一:∵ |AB| = |BC| = |AC| = = ∴ A≈84° 解法二:∵ =(–8,3),=(–2,–4) ∴ cosA==,∴ A≈84° 例4 设=(x1, y1) =(x2, y2) 与的夹角为q (0≤q≤p), 求证:x1x2+ y1y2=||||cosq 证明:如图,设, 起点在原点,终点为A,B 则A=(x1, y1) B=(x2, y2) =- 在△ABC中,由余弦定理 |-|2=||2+||2-2|||| cosq ∵|-|2=||2=|(x2-x1, y2-y1)|2=(x2-x1)2+( y2-y1)2 ||2=x12+y12 ,||2= x22+y22 ∴(x2-x1)2+( y2-y1)2= x12+y12+ x22+y22-2|||| cosq ∴x1x2+ y1y2=||||cosq 即有•= x1x2+ y1y2=||||cosq 四、课堂练习: 1在△ABC中,bCosA=acosB,则三角形为( ) A直角三角形 B锐角三角形C等腰三角形D等边三角形 2在△ABC中,若a2>b2+c2,则△ABC为;若a2=b2+c2,则△ABC为 ;若a2<b2+c2且b2<a2+c2且c2<a2+b2,则△ABC为 3在△ABC中,sinA=2cosBsinC,则三角形为 4在△ABC中,BC=3,AB=2,且,A= 参考答案: 1C 2钝角三角形,直角三角形,锐角三角形 3等腰三角形 4120° 五、小结 余弦定理及其应用 六、课后作业: 1在△ABC中,证明下列各式: (1)(a2-b2-c2)tanA+(a2-b2+c2)tanB=0 (2) 证明:(1)左边=(a2-b2-c2) 故原命题得证 故原命题得证 2在△ABC中,已知sinB·sinC=cos2,试判断此三角形的类型 解:∵sinB·sinC=cos2, ∴sinB·sinC= ∴2sinB·sinC=1+cos[180°-(B+C)] 将cos(B+C)=cosBcosC-sinBsinC代入上式得 cosBcosC+sinBsinC=1, ∴cos(B-C)=1 又0<B,C<π,∴-π<B-C<π∴B-C=0 ∴B=C 故此三角形是等腰三角形 3在△ABC中,bcosA=acosB试判断三角形的形状 解法一:利用余弦定理将角化为边 ∵bcosA=acosB,∴b· ∴b2+c2-a2=a2+c2-b2,∴a2=b2,∴a=b,故此三角形是等腰三角形 解法二:利用正弦定理将边转化为角∵bcosA=acosB 又b=2RsinB,a=2RsinA,∴2RsinBcosA=2RsinAcosB ∴sinAcosB-cosAsinB=0∴sin(A-B)=0 ∵0<A,B<π,∴-π<A-B<π,∴A-B=0 即A=B 故此三角形是等腰三角形 七、板书设计(略) 八、课后记: 查看更多