- 2021-06-10 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
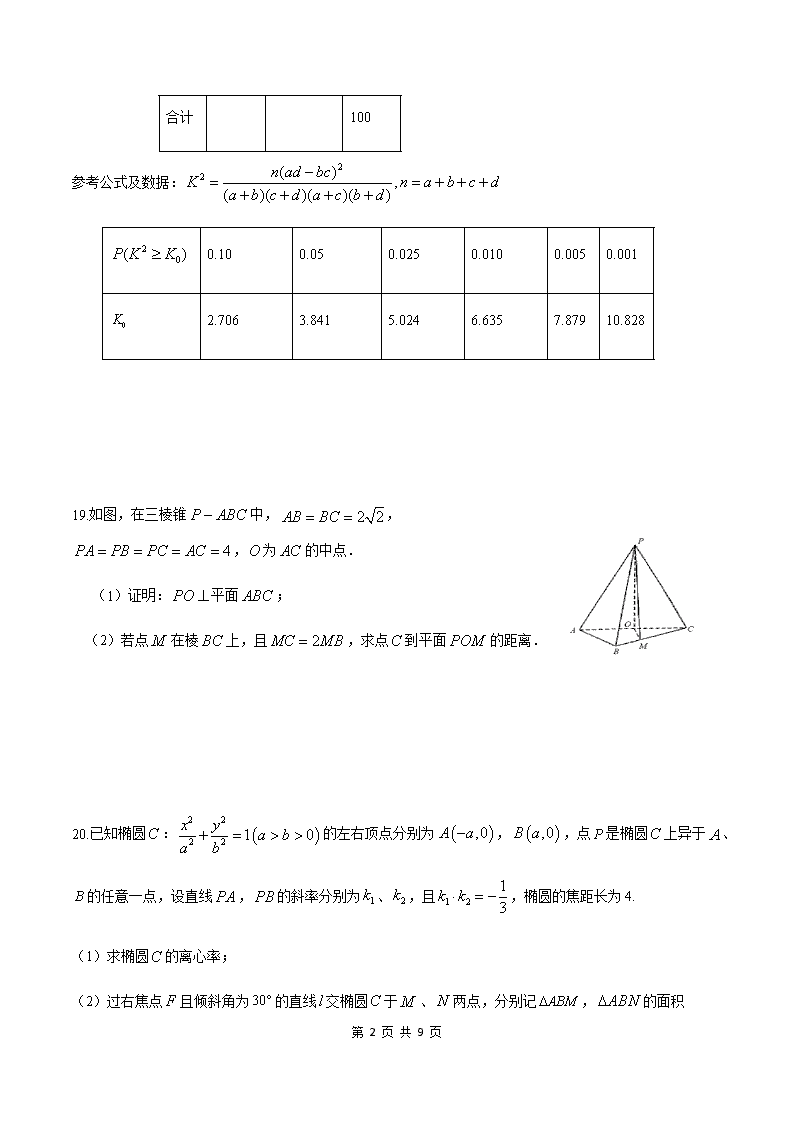
2020届高三数学(文)“大题精练”2
2020届高三数学(文)“大题精练”2 17.已知等比数列的各项均为正数,为等比数列的前项和,若,. (1)恒成立,求的最小值; (2)设,求数列的前项和. 18.为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:,,,,,,得到如图所示的频率分布直方图. (1)求的值; (2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表); (3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”? 优秀 非优秀 合计 男生 40 女生 50 第 9 页 共 9 页 合计 100 参考公式及数据: 0.10 0.05 0.025 0.010 0.005 0.001 2.706 3.841 5.024 6.635 7.879 10.828 19.如图,在三棱锥中,,,为的中点. (1)证明:平面; (2)若点在棱上,且,求点到平面的距离. 20.已知椭圆:的左右顶点分别为,,点是椭圆上异于、的任意一点,设直线,的斜率分别为、,且,椭圆的焦距长为4. (1)求椭圆的离心率; (2)过右焦点且倾斜角为的直线交椭圆于、两点,分别记,的面积 第 9 页 共 9 页 为、,求的值. 21.在直角坐标系中,曲线的参数方程为(为参数),以原点为极点,以轴正半轴为极轴,建立极坐标系,曲线的极坐标方程为. (1)判断曲线与曲线的位置关系;(2)设点为曲线上任意一点,求的最大值. 22.已知实数正数x, y满足. (1)解关于x的不等式; (2)证明: 第 9 页 共 9 页 2020届高三数学(文)“大题精练”2(答案解析) 17.已知等比数列的各项均为正数,为等比数列的前项和,若,. (1)恒成立,求的最小值; (2)设,求数列的前项和. 【解】(1)因为为等比数列,所以,所以,,所以, 又,所以,所以, 因为恒成立,所以,即的最小值是3. (2)由(1)可知,所以, 故 ① ② ① -②得:, 整理得, 18.为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:,,,,,,得到如图所示的频率分布直方图. (1)求的值; 第 9 页 共 9 页 (2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表); (3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”? 优秀 非优秀 合计 男生 40 女生 50 合计 100 参考公式及数据: 0.10 0.05 0.025 0.010 0.005 0.001 2.706 3.841 5.024 6.635 7.879 10.828 【解】(1)由题可得 ,解得. (2)平均成绩为: (3)由(2)知,在抽取的名学生中,比赛成绩优秀的有人,由此可得完整的列联表: 优秀 非优秀 合计 男生 女生 第 9 页 共 9 页 合计 ∵的观测值, ∴没有的把握认为“比赛成绩是否优秀与性别有关”. 19.如图,在三棱锥中,,,为的中点. (1)证明:平面; (2)若点在棱上,且,求点到平面的距离. 【解】(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=. 连结OB.因为AB=BC=,所以△ABC为等腰直角三角形,且OB⊥AC,OB==2. 由知,OP⊥OB.由OP⊥OB,OP⊥AC知PO⊥平面ABC. (2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,所以CH⊥平面POM. 故CH的长为点C到平面POM的距离. 由题设可知OC==2,CM==,∠ACB=45°. 所以OM=,CH==. 所以点C到平面POM的距离为. 20.已知椭圆:的左右顶点分别为,,点是椭圆上异于、 第 9 页 共 9 页 的任意一点,设直线,的斜率分别为、,且,椭圆的焦距长为4. (1)求椭圆的离心率; (2)过右焦点且倾斜角为的直线交椭圆于、两点,分别记,的面积 为、,求的值. 【解】(1)设点,则,①∵,② ∴联立①②得,∴,∴,∴. (2)由题意知,,即,由(1)知,,∴, ∴,,∴椭圆的方程为:,由已知得:. 联立,可得.设,,根据韦达定理,得, 于是. 21.在直角坐标系中,曲线的参数方程为(为参数),以原点为极点,以轴正半轴为极轴,建立极坐标系,曲线的极坐标方程为. (1)判断曲线与曲线的位置关系; (2)设点为曲线上任意一点,求的最大值. 第 9 页 共 9 页 【解】(1)消去得的普通方程为,由得, ∴,即,化为标准方程为, 即曲线是以为圆心,半径为1的圆,圆心到直线的距离,故曲线与曲线相交. (2)由为曲线上任意一点,可设, 则,其中, ∴的最大值是. 22.已知实数正数x, y满足. (1)解关于x的不等式; (2)证明: 【解】(1) ,解得,所以不等式的解集为 第 9 页 共 9 页 (2)解法1: 且, . 当且仅当时,等号成立. 解法2: 且, , 当且仅当时,等号成立. 第 9 页 共 9 页查看更多