- 2021-06-10 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
专题02+集合与常用逻辑用语+常用逻辑用语-2019年高考数学(理)高频考点名师揭秘与仿真测试
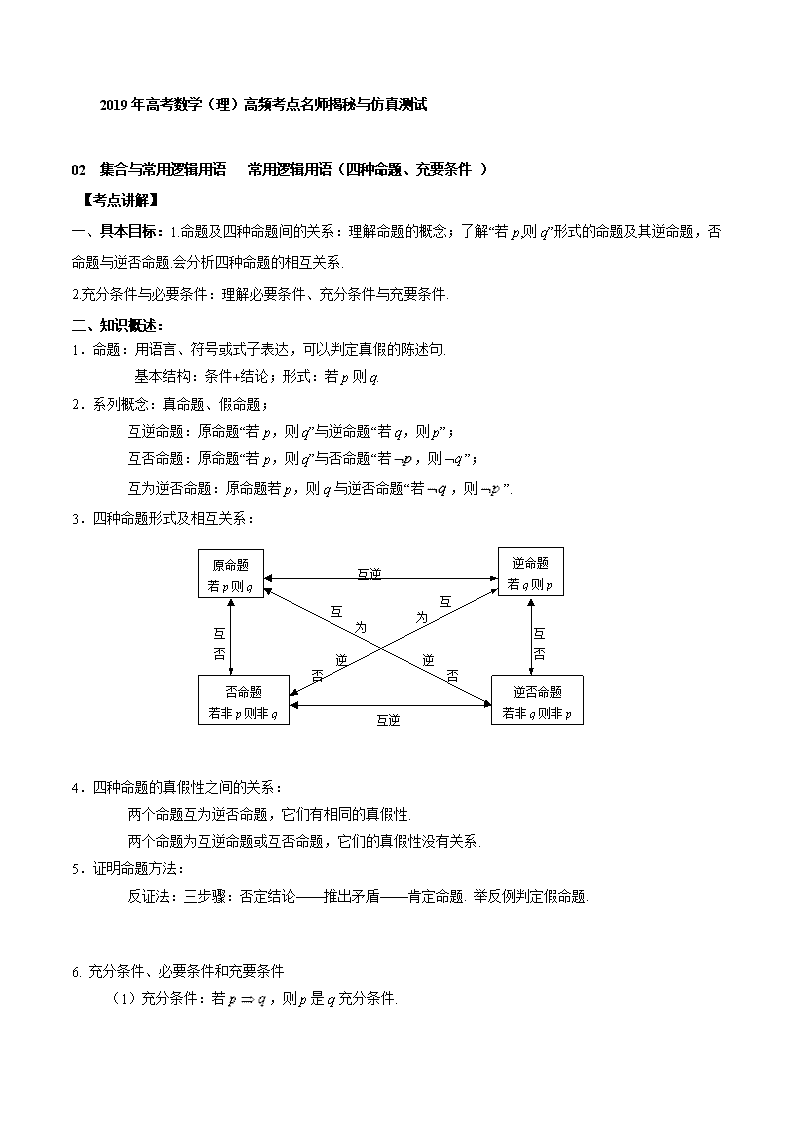
2019年高考数学(理)高频考点名师揭秘与仿真测试 02 集合与常用逻辑用语 常用逻辑用语(四种命题、充要条件 ) 【考点讲解】 一、 具本目标:1.命题及四种命题间的关系:理解命题的概念;了解“若p,则q”形式的命题及其逆命题,否命题与逆否命题.会分析四种命题的相互关系. 2.充分条件与必要条件:理解必要条件、充分条件与充要条件. 二、知识概述: 1.命题:用语言、符号或式子表达,可以判定真假的陈述句. 基本结构:条件+结论;形式:若p则q. 2.系列概念:真命题、假命题; 互逆命题:原命题“若p,则q”与逆命题“若q,则p”; 互否命题:原命题“若p,则q”与否命题“若,则”; 互为逆否命题:原命题若p,则q与逆否命题“若,则”. 3.四种命题形式及相互关系: 原命题 若p则q 逆命题 若q则p 否命题 若非p则非q 逆否命题 若非q则非p 互逆 互逆 互 否 互 否 互 为 逆 否 互 为 逆 否 4.四种命题的真假性之间的关系: 两个命题互为逆否命题,它们有相同的真假性. 两个命题为互逆命题或互否命题,它们的真假性没有关系. 5.证明命题方法: 反证法:三步骤:否定结论——推出矛盾——肯定命题. 举反例判定假命题. 6. 充分条件、必要条件和充要条件 (1)充分条件:若,则p是q充分条件. (2)必要条件:若,则p是q必要条件 (3)充要条件:若,且,则p是q充要条件,即: p的q充分不必要条件:,且q p p的q必要不充分条件:qq,且p q p的q既不充分又不必要条件:p q且q p 注:如果甲是乙的充分条件,则乙是甲的必要条件;反之亦然. 7.判断充分条件和必要条件的方法 (1)命题判断法: 设“若p,则q”为原命题,那么: ①原命题为真,逆命题为假时,p是q的充分不必要条件; ②原命题为假,逆命题为真时,p是q的必要不充分条件; ③原命题与逆命题都为真时,p是q的充要条件; ④原命题与逆命题都为假时,p是q的既不充分也不必要条件. (2)集合判断法: 从集合的观点看,建立命题p,q相应的集合:p:A={x|p(x)成立},q:B={x|q(x)成立},那么: ①若A⊆B,则p是q的充分条件;若A是B的真子集时,则p是q的充分不必要条件; ②若B⊆A,则p是q的必要条件;若B真子集A时,则p是q的必要不充分条件; ③若A⊆B且B⊆A,即A=B时,则p是q的充要条件. (3)等价转化法: p是q的什么条件等价于非q是非p的什么条件. 【真题分析】 1.(15山东理)若“,”是真命题,则实数的最小值为_________. 【解析】本题考查的是命题的定义与正切函数的综合应用,其中要求考生对全称命题,正切函数的性质运用,不等式恒成立问题的解决特点要熟练掌握,若“ ”是真命题,则大于或等于函数在的最大值,因为函数在上为增函数,所以,函数在上的最大值为1,所以, ,也就是实数 的最小值为1. 【答案】1 【变式】下列命题是真命题的为( ) A.若,则 B.若,则 C.若,则 D.若,则 【答案】A 2.(15山东文)设,命题“若,则方程有实根”的逆否命题是( ) A.若方程有实根,则 B.若方程有实根,则 C.若方程没有实根,则 D.若方程没有实根,则 【解析】本题考点是四种命题的形式,要求掌握四种命题的表达方式及与原命题的关系,正确理解“否定”的内容.一个命题的逆否命题,要将原命题的条件、结论加以否定,并且加以互换. 【答案】D 3.(2018天津卷4)设,则“”是“”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 【解析】本题考查的是由两个不等式的解集之间的关系来判断两个命题之间的关系,这就要求会解两个不等式求出来两个不等式的解集.然后利用集合间的关系来判断两个命题之间的关系. 由可以得到,,即.由可得,.很显然前者成立后者一定成成立,前者是后者的充分条件,后者成立未必有前者成立,所以前者是后者的充分不必要条件.从集合的角度来判断这两个命题的关系就是前者是后者的真子集,那么就是充分不必要条件. 【答案】A 【变式】【2018浙江卷6】已知平面α,直线m,n满足mα,nα,则“m∥n”是“m∥α”的 A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 【答案】A 4.【2016高考天津文数】设,,则“”是“”的( ) A.充要条件 B.充分而不必要条件 C.必要而不充分条件 D.既不充分也不必要条件 【解析】本题考查的是命题间的充要关系,根据本题的特点,可以用验证法用特列例子来否定命题的不成 立性,同时也要用普遍性证明命题的正确性,比如,即“”是“”未必成立,所以充分性不成立;而,必要性成立. 【答案】C 【变式】函数在处导数存在,若;是的极值点,则( ) A.是的充分必要条件 B. 是的充分条件,但不是的必要条件 C. 是的必要条件,但不是的充分条件 D. 既不是的充分条件,也不是的必要条件 【答案】C 5.(2018北京卷6)设均为单位向量,则“”是“⊥”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 【解析】本题考查的是向量垂直的判定,这里要根据向量的数量积运算及充分条件与必要条件的对应来判断.将原等式两边平方进行向量的运算并整理可以得到两向量的数量积为零,从而判断两向量垂直. 由可得,整理得,也就是 ,即为⊥,所以均为单位向量,且是⊥的充要条件. 【答案】C. 【变式】【2015高考四川,文4】设a,b为正实数,则“a>b>1”是“log2a>log2b>0”的( ) A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件 【解析】本题考查对数函数的概念和性质、充要条件等基本概念,考查学生综合运用数学知识和方法解决问题的能力.判断条件的充要性,必须从“充分性”和“必要性”两个方向分别判断,同时注意涉及的相关 概念和方法.本题中涉及对数函数基本性质——单调性和函数值的符号,因此可以结合对数函数的图象进行判断,从而得出结论.a>b>1时,有log2a>log2b>0成立,反之当log2a>log2b>0成立时,a>b>1也正确.选A 【答案】A 6.(16北京理),是向量,则“”是“”的( ) A.充分不必要条件 B. 必要不充分条件 C.充分必要条件 D.既不充分又不必要条件 【答案】D 【变式】(2015高考浙江,文3)设,是实数,则“”是“”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 【解析】本题考查充分条件、必要条件、不等式的性质,验证方法可用特殊值法:当时,,但,故是不充分条件;当时,,但,故是不必要条件.所以“”是“”的即不充分也不必要条件.故选D. 【答案】D 7.(15浙江理)设,是有限集,定义,其中表示有限集中的元素个数. 命题①:对任意有限集,,“”是“”的充分必要条件; 命题②:对任意有限集,,,. A.命题①和命题②都成立 B.命题①和命题②都不成立 C.命题①成立,命题②不成立 D.命题①不成立,命题②成立 【答案】A. 8.已知命题:方程有两个不等的负根,命题:无实根,且为真命题,求实数的取值范围. 【分析】本题考查的是一元二次方程与命题的真假相结合的问题,因此在命题的要求下,利用二次方程根的情况来求待定参数时一定要准确应用所学知识解决问题. 【解析】由已知可知,,解得, ,解得 . 且为真,同时为真,则, ,实数的取值范围是. 【模拟考场】 1.已知,则“”是“”的( ) A.充分非必要条件 B.必要非充分条件 C.充要条件D.既非充分又非必要条件 【解析】由题意可知识时一定成立,反之则不一定,比如时.但不成立. 【答案】A 2.“”是“”的( ) A.充分必要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分又不必要条件 【答案】A 3.设,则“”是“”的( ) A.充分不必要条件 B. 必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 【解析】,所以“”是“”的充分非必要条件,选A. 【答案】A 4.已知,,,为实数,且>.则“>”是“->-”的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件 【解析】显然,充分性不成立.又,若->-和>都成立,则同向不等式相加得> 即由“->-”“>” 【答案】B 5.设,是两个集合,则“”是“”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件 【解析】由题意得,,反之,,故为充要条件,选C. 【答案】C. 6.在中,角..所对应的变分别为..,则是的( ) A.充分必要条件 B.充分非必要条件 C.必要非充分条件 D.非充分非必要条件 【答案】A 7.设p:x<3,q:-1查看更多
相关文章
- 当前文档收益归属上传用户