2020高中数学函数的表示法

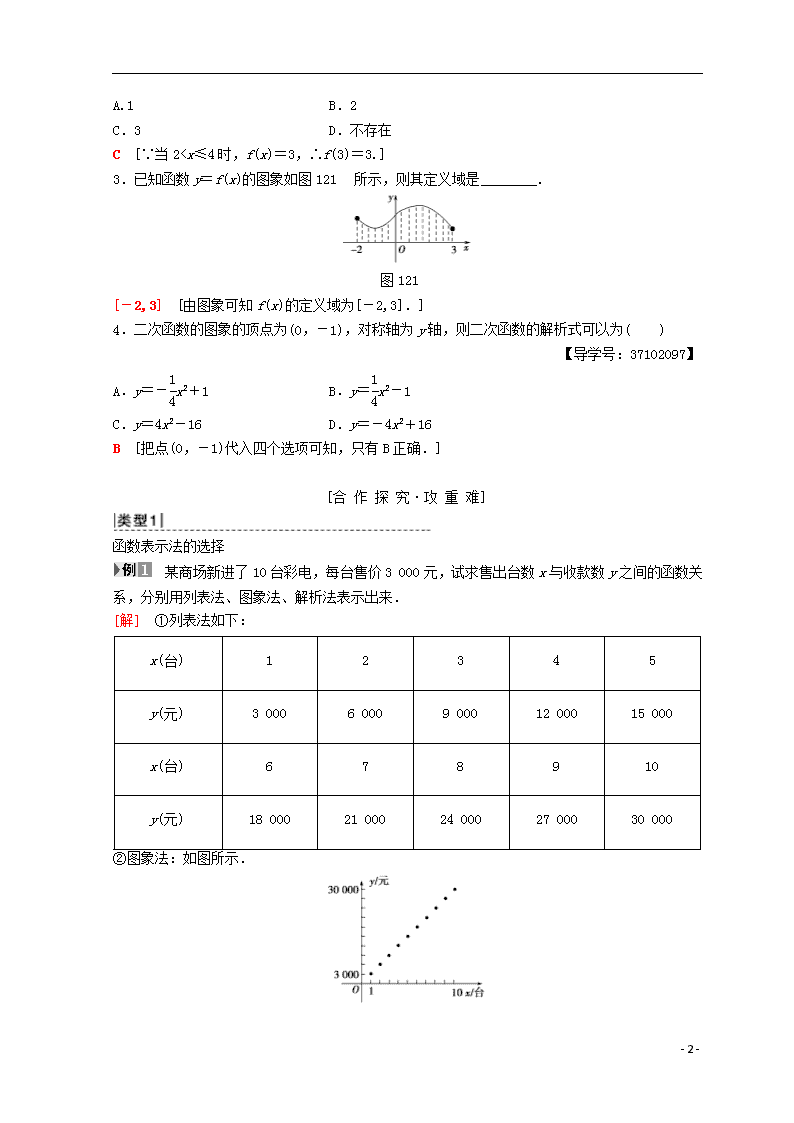
2020高中数学函数的表示法

第1课时　函数的表示法 学习目标：1.掌握函数的三种表示方法：解析法、图象法、列表法．(重点)2.会根据不同的需要选择恰当的方法表示函数．(难点)‎ ‎[自 主 预 习·探 新 知]‎ 函数的表示法 思考：(1)函数的三种表示方法各有什么优、缺点？‎ ‎(2)任何一个函数都可以用解析法、列表法、图表法三种形式表示吗？‎ ‎[提示]　(1)三种表示方法的优、缺点比较：‎ 优点 缺点 解析法 ‎①简明、全面地概括了变量间的关系；②可以通过解析式求出任意一个自变量所对应的函数值 不够形象、直观 列表法 不通过计算就可以直接看出与自变量的值相对应的函数值 一般只能表示部分自变量的函数值 图象法 直观、形象地表示出函数的变化情况，有利于通过图形研究函数的某些性质 只能近似地求出自变量所对应的函数值，有时误差较大 ‎(2)不一定．‎ 并不是所有的函数都可以用解析式表示，不仅如此，图象法也不适用于所有函数，如D(x)＝列表法虽在理论上适用于所有函数，但对于自变量有无数个取值的情况，列表法只能表示函数的一个概况或片段．‎ ‎[基础自测]‎ ‎1．思考辨析 ‎(1)任何一个函数都可以用列表法表示．(　　)‎ ‎(2)任何一个函数都可以用解析法表示．(　　)‎ ‎(3)函数的图象一定是其定义区间上的一条连续不断的曲线．(　　)‎ ‎[答案]　(1)×　(2)×　(3)×‎ ‎2．已知函数f(x)由下表给出，则f(3)等于(　　)‎ x ‎1≤x<2‎ ‎2‎ ‎21，或x<－1). ‎ ‎【导学号：37102099】‎ ‎[解]　(1)y＝x＋1(x≤0)表示一条射线，图象如图(1)．‎ ‎(2)y＝x2－2x＝(x－1)2－1(x>1，或x<－1)是抛物线y＝x2－2x去掉－1≤x≤1之间的部分后剩余曲线．如图(2)．‎ 解析式的求法 ‎[探究问题]‎ ‎1．已知函数的类型(如二次函数)，常用什么方法求其解析式？‎ 提示：常用待定系数法，如二次函数常有三种设法：‎ ‎(1)一般式：f(x)＝ax2＋bx＋c，(a≠0)；‎ ‎(2)顶点式：f(x)＝a(x－h)2＋k，(a≠0)；‎ ‎(3)交点式：f(x)＝a(x－x1)(x－x2)，其中x1，x2是图象与x轴交点的横坐标．‎ ‎2．已知f(x)的解析式，我们可以用代入法求f(g(x))，反之，若已知f(g(x))，如何求f(x)．‎ 提示：若已知f(g(x))的解析式，我们可以用换元法或配凑法求f(x)．‎ ‎　(1)已知f(＋1)＝x－2，则f(x)＝________；‎ ‎(2)已知函数f(x)是一次函数，若f(f(x))＝4x＋8，则f(x)＝________.‎ ‎(3)已知函数f(x)对于任意的x都有f(x)－‎2f(－x)＝1＋2x，则f(x)＝________. ‎ ‎【导学号：37102100】‎ 思路探究：(1)用换元法或配凑法求解；(2)用待定系数法求解；(3)用方程组法求解．‎ - 8 -‎ ‎(1)x2－4x＋3(x≥1)　(2)2x＋或－2x－8　(3)x－1　[(1)法一(换元法)：令t＝＋1，则t≥1，x＝(t－1)2，代入原式有f(t)＝(t－1)2－2(t－1)＝t2－4t＋3，f(x)＝x2－4x＋3(x≥1)．‎ 法二(配凑法)：f(＋1)＝x＋2＋1－4－4＋3＝(＋1)2－4(＋1)＋3，‎ 因为＋1≥1，‎ 所以f(x)＝x2－4x＋3(x≥1)．‎ ‎(2)设f(x)＝ax＋b(a≠0)，‎ 则f(f(x))＝f(ax＋b)＝a(ax＋b)＋b＝a2x＋ab＋b.‎ 又f(f(x))＝4x＋8，‎ 所以a2x＋ab＋b＝4x＋8，‎ 即解得或 所以f(x)＝2x＋或f(x)＝－2x－8.‎ ‎(3)由题意，在f(x)－‎2f(－x)＝1＋2x中，以－x代x可得f(－x)－‎2f(x)＝1－2x，联立可得消去f(－x)可得f(x)＝x－1.]‎ 母题探究：1.(变条件)把本例(2)的题干改为“已知函数f(x)是二次函数，且f(0)＝1，f(x＋1)－f(x)＝2x.”求f(x)的解析式．‎ ‎[解]　设f(x)＝ax2＋bx＋c，由f(0)＝1得c＝1.‎ 又f(x＋1)＝a(x＋1)2＋b(x＋1)＋1，‎ ‎∴f(x＋1)－f(x)＝2ax＋a＋b.‎ 由2ax＋a＋b＝2x，得 解得a＝1，b＝－1.‎ ‎∴f(x)＝x2－x＋1.‎ ‎2．(变条件)把本例(3)的题干改为“‎2f＋f(x)＝x(x≠0)”，求f(x)的解析式．‎ ‎[解]　f(x)＋‎2f＝x，令x＝，‎ 得f＋‎2f(x)＝.‎ 于是得关于f(x)与f的方程组 解得f(x)＝－(x≠0)．‎ ‎[规律方法]　求函数解析式的四种常用方法 ‎1．待定系数法：若已知f(x)的解析式的类型，设出它的一般形式，根据特殊值确定相关的系数即可．‎ 2．换元法：设t＝g(x)，解出x，代入f(g(x))，求f(t)的解析式即可．‎ - 8 -‎ 3．配凑法：对f(g(x))的解析式进行配凑变形，使它能用g(x)表示出来，再用x代替两边所有的“g(x)”即可．‎ 4．方程组法：当同一个对应关系中的两个之间有互为相反数或互为倒数关系时，可构造方程组求解．‎ 提醒：应用换元法求函数解析式时，务必保证函数在换元前后的等价性．‎ ‎[当 堂 达 标·固 双 基]‎ ‎1．已知函数f(x＋1)＝3x＋2，则f(x)的解析式是(　　)‎ ‎【导学号：37102101】‎ A．f(x)＝3x－1　　　　　　 B．f(x)＝3x＋1‎ C．f(x)＝3x＋2 D．f(x)＝3x＋4‎ A　[令x＋1＝t，则x＝t－1，∴f(t)＝3(t－1)＋2＝3t－1.∴f(x)＝3x－1.]‎ ‎2．由下表给出函数y＝f(x)，则f(f(1))等于(　　)‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ y ‎4‎ ‎5‎ ‎3‎ ‎2‎ ‎1‎ A.1 B．2‎ C．4 D．5‎ B　[由题表可知f(1)＝4，∴f(f(1))＝f(4)＝2.]‎ ‎3．若一个长方体的高为‎80 cm，长比宽多‎10 cm，则这个长方体的体积y(cm3)与长方体的宽x(cm)之间的表达式是________. ‎ ‎【导学号：37102102】‎ y＝80x(x＋10)，x∈(0，＋∞)　[由题意可知，长方体的长为(x＋10)cm，从而长方体的体积y＝80x(x＋10)，x>0.]‎ ‎4．f(x)的图象如图122所示，则f(x)的值域为________．‎ 图122‎ ‎[－4,3]　[由函数的图象可知，f(x)的值域为[－2,3]∪[－4,2.7]，即[－4,3]．]‎ ‎5．已知函数f(x)＝x2－2x(－1≤x≤2)．‎ ‎(1)画出f(x)图象的简图；‎ ‎(2)根据图象写出f(x)的值域. ‎ ‎【导学号：37102103】‎ - 8 -‎ ‎[解]　(1)f(x)图象的简图如图所示．‎ ‎(2)观察f(x)的图象可知，f(x)图象上所有点的纵坐标的取值范围是[－1,3]，‎ 即f(x)的值域是[－1,3]．‎ - 8 -‎