高中数学必修4：3_1_1两角差的余弦公式(教、学案)

高中数学必修4：3_1_1两角差的余弦公式(教、学案)

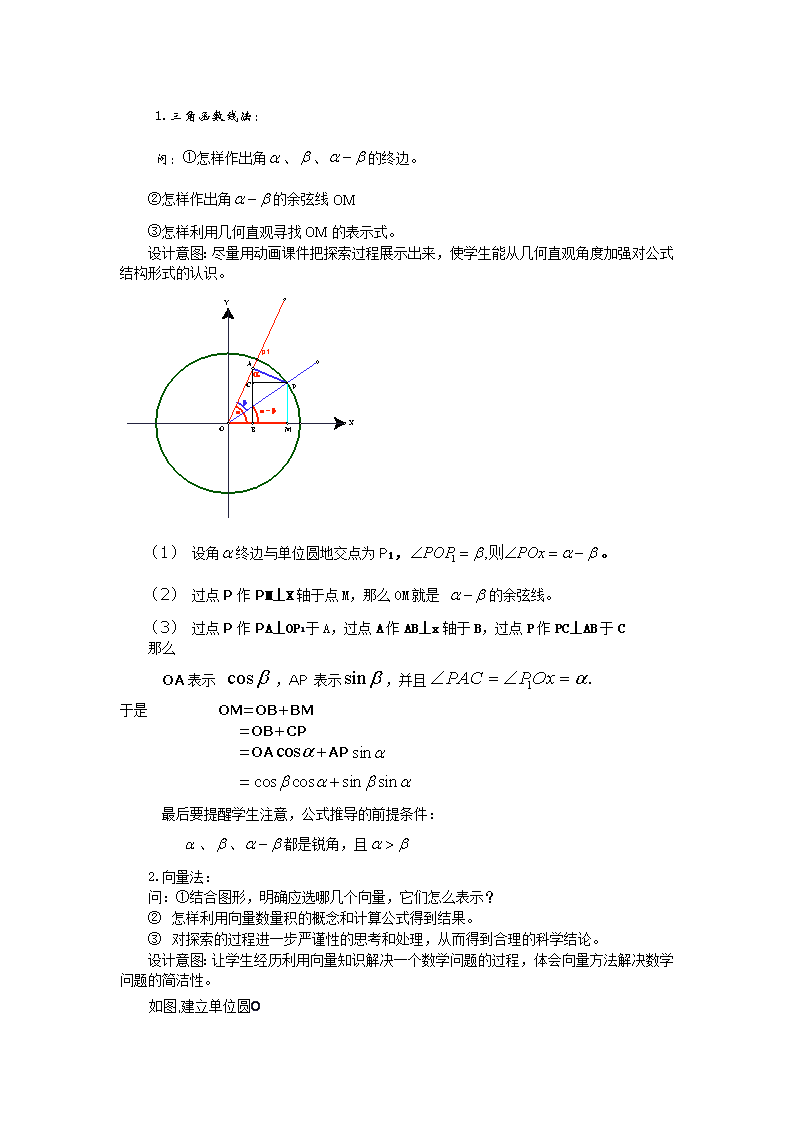
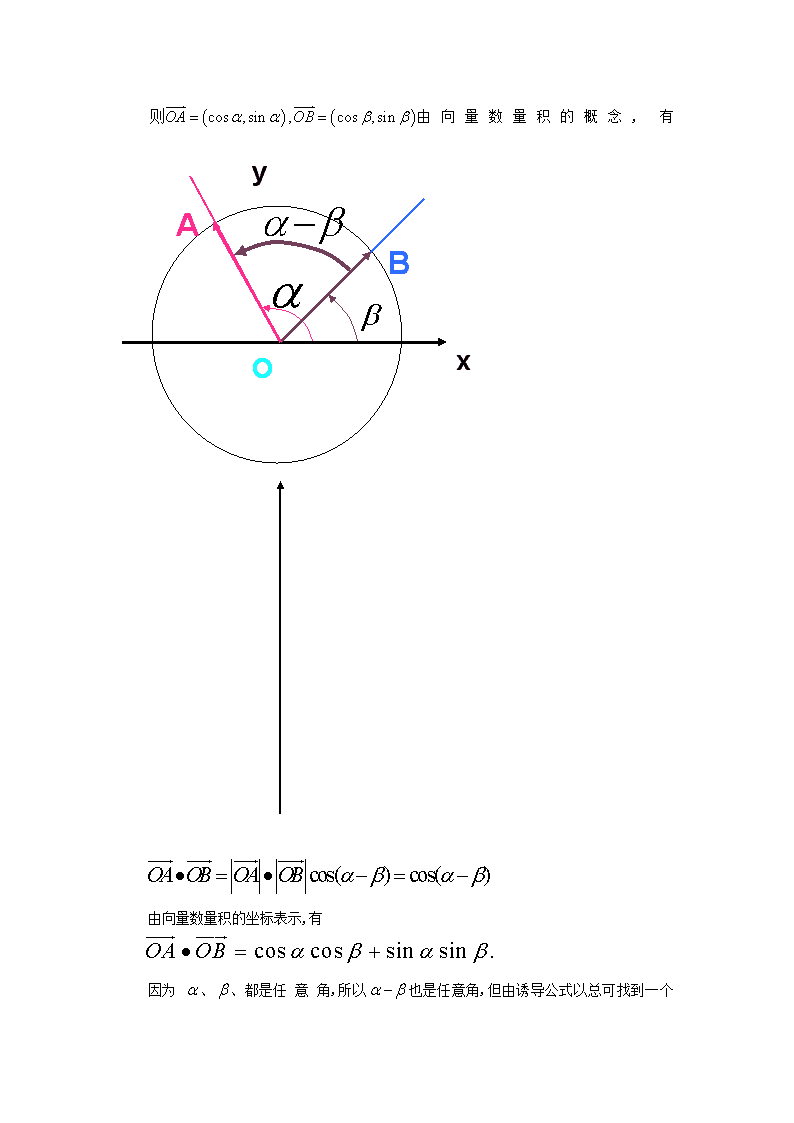
‎3. 1.1‎两角差的余弦公式 一、教材分析 ‎《两角差的余弦公式》是人教A版高中数学必修4第三章《三角恒等变换》第一节《两角和与差的正弦、余弦和正切公式》第一节课的内容。本节主要给出了两角差的余弦公式的推导，要引导学生主动参与，独立思索，自己得出相应的结论。‎ 二、教学目标 ‎1.引导学生建立两角差的余弦公式。通过公式的简单应用，使学生初步理解公式的结构 及其功能，并为建立其他和差公式打好基础。‎ ‎2.通过课题背景的设计，增强学生的应用意识，激发学生的学习积极性。‎ ‎3.在探究公式的过程中，逐步培养学生学会分析问题、解决问题的能力，培养学生学会合作交流的能力。‎ 三、教学重点难点 重点 两角差余弦公式的探索和简单应用。‎ 难点 探索过程的组织和引导。‎ 四、学情分析 之前学习了三角函数的性质，以及平面向量的运算和应用，在此基础上，要考虑如何利用任意角的正弦余弦值来表示，牢固的掌握这个公式，并会灵活运用公式进行下一节内容的学习。‎ 五、教学方法 ‎1.自主性学习法：通过自学掌握两角差的余弦公式.‎ ‎2.探究式学习法：通过分析、探索、掌握两角差的余弦公式的过程.‎ ‎3.反馈练习法：以练习来检验知识的应用情况，找出未掌握的内容及其存在的差距 六、课前准备 ‎1.学生准备：预习《两角差的余弦公式》，理解两种方法的推理过程。‎ ‎2.教师准备：课前预习学案，课内探究学案，课后延伸拓展学案。‎ 七、课时安排：1课时 八、教学过程 ‎（一）创设情景，揭示课题 ‎ 以学校教学楼为背景素材（见课件）引入问题。并针对问题中的用计算器或不用计算器计算求值，以激趣激疑，导入课题。‎ ‎ 教师问：想一想: 学校因某次活动的需要,需从楼顶的C点处往该点正对的地面上的A点处拉一条钢绳,为了在购买钢绳时不至于浪费,你能算一算到底需要多长钢绳吗? (要求在地面上测量,测量工具:皮尺,测角器)‎ 问题：（1）能不能不用计算器求值 ： ， ，‎ ‎（2）‎ 设计意图：由给出的背景素材，使学生感受数学源于生活，又应用于生活，唤起学生解决问题的兴趣，和抛出新知识引起学生的疑惑，在兴趣和疑惑中，激发学生的求知欲，引导学习方向。‎ ‎（二）、研探新知 ‎1.三角函数线法：‎ 问：①怎样作出角、、的终边。‎ ‎②怎样作出角的余弦线OM ‎③怎样利用几何直观寻找OM的表示式。‎ 设计意图：尽量用动画课件把探索过程展示出来，使学生能从几何直观角度加强对公式结构形式的认识。‎ （1） 设角终边与单位圆地交点为P1，。‎ （2） 过点P作PM⊥X轴于点M，那么OM就是 的余弦线。‎ （3） 过点P作PA⊥OP1于A，过点A作AB⊥x轴于B，过点P作PC⊥AB于C 那么 ‎ ‎ OA表示 ，AP 表示，并且 于是 OM=OB+BM ‎ =OB+CP ‎ =OA+AP ‎ =‎ ‎ 最后要提醒学生注意，公式推导的前提条件：‎ ‎、、都是锐角，且 ‎2.向量法：‎ 问：①结合图形，明确应选哪几个向量，它们怎么表示？‎ ② 怎样利用向量数量积的概念和计算公式得到结果。‎ ③ 对探索的过程进一步严谨性的思考和处理，从而得到合理的科学结论。‎ 设计意图：让学生经历利用向量知识解决一个数学问题的过程，体会向量方法解决数学问题的简洁性。‎ 如图,建立单位圆O ‎ 由向量数量积的概念,有A O B x y ‎ ‎ 由向量数量积的坐标表示,有 因为 、、都是任 意 角,所以也是任意角,但由诱导公式以总可找到一个 ‎，使得 。‎ ‎ 于是对于任意角、都有 ‎ ‎ 例1. 利用差角余弦公式求的值 ‎ ‎（求解过程让学生独立完成，注意引导学生多方向、多维度思考问题）‎ 解法1：‎ 解法2：‎ 变式训练：利用两角差的余弦公式证明下列诱导公式：‎ ‎（1）； （2）‎ ‎ （让学生联系公式和本题的条件，考虑清楚要计算，应作那些准备。） 解：由，得 又由，是第三象限角，得 所以 让学生结合公式，明确需要再求哪些三角函数值，可使问题得到解决。‎ 变式训练： ‎ ‎（三）、质疑答辩，排难解惑，发展思维 ‎ ‎1.利用两角和（差）的余弦公式，求 ‎【点评】：把一个具体角构造成两个角的和、差形式，有很多种构造方法，例如：，要学会灵活运用.‎ ‎2.求值 ‎ ‎3．化简 ‎ ‎ ‎ 提示：利用拆角思想的变换技巧 ‎（设计意图：通过变式训练，进一步加深学生对公式的理解和应用，体验公式既可正用、逆用，还可变用.还可使学生掌握“变角”和“拆角”的思想方法解决问题，培养了学生的灵活思维品质，提高学生的数学交流能力，促进思维的创新。） ‎ ‎ （四）发导学案、布置预习 本节我们学习了两角和与差的余弦公式，要求同学们掌握公式的推导，能熟练运用公式，注意公式的逆用。在解题过程中注意角、的象限，也就是符号问题，学会灵活运用.课下完成本节的课后练习以及课后延展作业，课本习题‎2.3.4‎ ‎(设计意图：布置下节课的预习作业，并对本节课巩固提高。教师课后及时批阅本节的延伸拓展训练。)‎ 九、板书设计 两角差的余弦公式 ‎1.三角函数线法 2.向量法 例1 变式训练 例2 变式训练 当堂训练1. 2.‎ 3. ‎4.‎ 十、教学反思 本节主要考察如何用任意角的正弦余弦值来表示，回顾公式 的推导过程，观察公式的特征，注意符号区别以及公式中角，的任意性，特别要注意公式既可正用、逆用，还可变用(即要活用).还要注意掌握“变角”和“拆角”的思想方法解决问题.‎ 设计意图：让学生通过自己小结，反思学习过程，加深对公式及其推导过程（包括发现、‎ 猜想、论证的数学化的过程）的理解。‎ ‎ 十一、学案设计(见下页)‎ ‎3.1.1‎两角差的余弦公式 课前预习学案 一、预习目标 预习《两角差的余弦公式》，体会两角差的余弦公式的推导过程 ，尤其是向量法的运用。‎ 二、 预习内容 阅读课本相关内容，经历用向量的数量积推导出两角差的余弦公式，进一步体会向量方法作用，并回答以下问题：‎ 1. 如何用任意角的正弦余弦值来表示；‎ 2. 如何求出的值;‎ 3. 会求的值吗？‎ 三、 提出疑惑 疑惑点 疑惑内容 课内探究学案 一、 学习内容 通过公式的简单应用，使学生初步理解公式的结构及其功能，并为建立其他和差公式打 好基础。‎ 二、 学习过程 ‎ 探究一：（1）能不能不用计算器求值 ： ， ，‎ ‎（2）‎ 探究二：两角差的余弦公式的推导 ‎1.三角函数线法：‎ 问：①怎样作出角、、的终边。‎ ‎②怎样作出角的余弦线OM ‎③怎样利用几何直观寻找OM的表示式。‎ ‎2.向量法：‎ 问：①结合图形，明确应选哪几个向量，它们怎么表示？‎ ② 怎样利用向量数量积的概念和计算公式得到结果。‎ ③ 对探索的过程进一步严谨性的思考和处理，从而得到合理的科学结论。‎ ‎ 例题整理 例1. 利用差角余弦公式求的值 ‎ 变式训练：利用两角差的余弦公式证明下列诱导公式：‎ ‎（1）； （2）‎ 变式训练：。‎ 一、 反思总结 本节主要考察如何用任意角的正弦余弦值来表示，回顾公式 的推导过程，观察公式的特征，注意符号区别以及公式中角，的任意性，特别要注意公式既可正用、逆用，还可变用(即要活用).在求值的过程中，还要注意掌握“变角”和“拆角”的思想方法解决问题.‎ 二、 当堂检测 ‎1.利用两角和（差）的余弦公式，求 ‎2.求值 ‎ ‎3．化简 ‎ 课后练习与提高 一、选择题 ‎1. 的值为 （ ）‎ A. B. C. D. ‎ ‎2. 的值为 （ ）‎ A. B. C. D .‎ ‎3.已知，则的值等于（ ）‎ A. B. C. D. ‎ 二、填空题 ‎4.化简= ‎ ‎5.若，则= ‎ 三、解答题、‎ ‎6.已知，求的值.‎