2021届高考数学一轮总复习第二章函数导数及其应用课时作业14导数与函数的单调性含解析苏教版
课时作业14 导数与函数的单调性
一、选择题
1.函数f(x)=x2-2lnx的单调递减区间是( A )
A.(0,1) B.(1,+∞)
C.(-∞,1) D.(-1,1)
解析:∵f′(x)=2x-=(x>0),
∴当x∈(0,1)时,f′(x)<0,f(x)为减函数;
当x∈(1,+∞)时,f′(x)>0,f(x)为增函数.
2.(2020·济南调研)已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是( C )
A.f(b)>f(c)>f(d)
B.f(b)>f(a)>f(e)
C.f(c)>f(b)>f(a)
D.f(c)>f(e)>f(d)
解析:由题意得,x∈(-∞,c)时,f′(x)>0,
所以函数f(x)在(-∞,c)上是增函数,
因为a
f(b)>f(a),故选C.
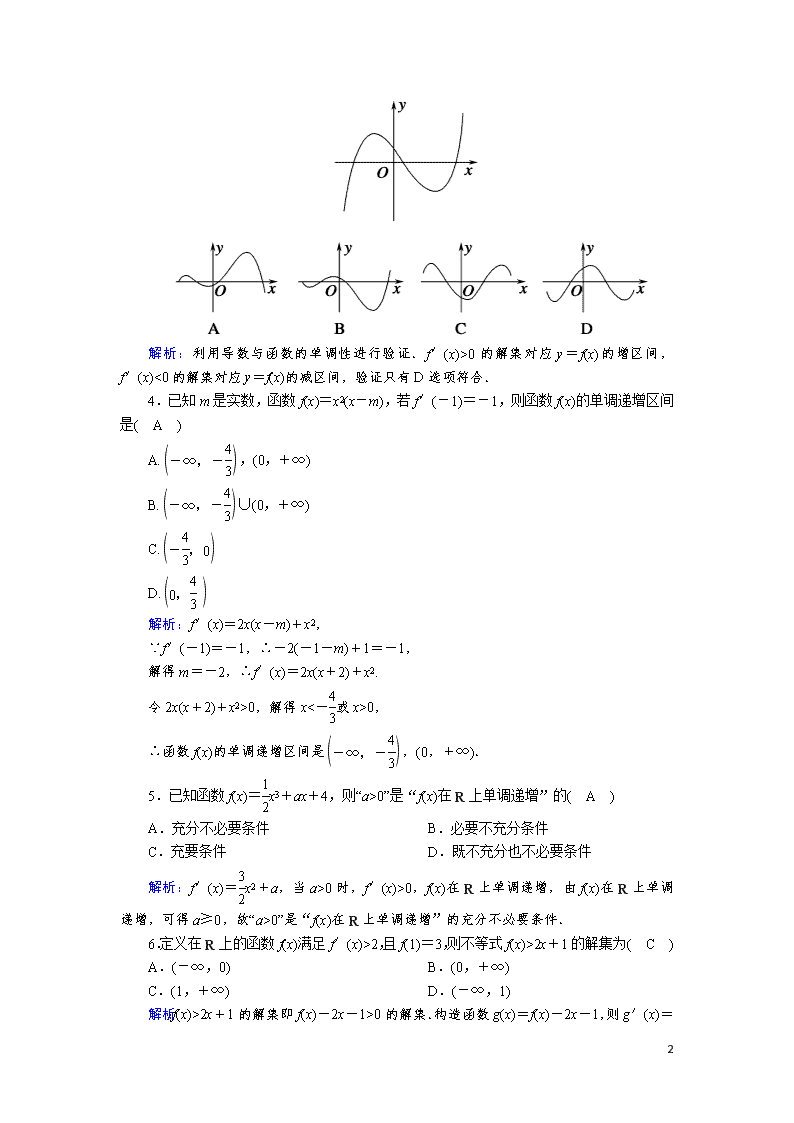
3.函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是( D )
6
解析:利用导数与函数的单调性进行验证.f′(x)>0的解集对应y=f(x)的增区间,f′(x)<0的解集对应y=f(x)的减区间,验证只有D选项符合.
4.已知m是实数,函数f(x)=x2(x-m),若f′(-1)=-1,则函数f(x)的单调递增区间是( A )
A.,(0,+∞)
B.∪(0,+∞)
C.
D.
解析:f′(x)=2x(x-m)+x2,
∵f′(-1)=-1,∴-2(-1-m)+1=-1,
解得m=-2,∴f′(x)=2x(x+2)+x2.
令2x(x+2)+x2>0,解得x<-或x>0,
∴函数f(x)的单调递增区间是,(0,+∞).
5.已知函数f(x)=x3+ax+4,则“a>0”是“f(x)在R上单调递增”的( A )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:f′(x)=x2+a,当a>0时,f′(x)>0,f(x)在R上单调递增,由f(x)在R上单调递增,可得a≥0,故“a>0”是“f(x)在R上单调递增”的充分不必要条件.
6.定义在R上的函数f(x)满足f′(x)>2,且f(1)=3,则不等式f(x)>2x+1的解集为( C )
A.(-∞,0) B.(0,+∞)
C.(1,+∞) D.(-∞,1)
解析:f(x)>2x+1的解集即f(x)-2x-1>0的解集.构造函数g(x)=f(x)-2x-1,则g′(x)=f′(x)-2,因为f′(x)>2,所以g′(x)=f′(x)-2>0,所以g(x)=f(x)-2x-1在R
6
上单调递增,且g(1)=f(1)-2-1=0,所以f(x)-2x-1>0的解集为(1,+∞),即不等式f(x)>2x+1的解集为(1,+∞).故选C.
7.(2020·山东济南质检)若函数f(x)=2x2-lnx在其定义域的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( C )
A.[1,+∞) B.[1,2)
C.[1,) D.[,2)
解析:f′(x)=4x-=,
令f′(x)>0,得x>;令f′(x)<0,得00.若a=f,b=0,c=-f,则a,b,c的大小关系是( A )
A.a0在(0,π)上恒成立,
所以g′(x)=f′(x)cosx-f(x)sinx>0在(0,π)上恒成立,
所以g(x)在(0,π)上单调递增,
所以gxf′(x)恒成立,则x2f-f(x)>0的解集为(1,+∞).
解析:当x∈(0,+∞)时,f(x)>xf′(x)⇔xf′(x)-f(x)<0⇔′<0.令g(x)=,则函数g(x)在(0,+∞)上单调递减.又当x∈(0,+∞)时,不等式x2f-f(x)>0⇔>,则0<0.
(1)当m=2时,求f(x)的极大值;
(2)试讨论f(x)在区间(0,1)上的单调性.
解:(1)当m=2时,f(x)=lnx+-x,
f′(x)=--1=-(x>0),
当02时,f′(x)<0,
当0,
∴f(x)在(0,)和(2,+∞)上单调递减,在(,2)上单调递增,∴f(x)的极大值为f(2)=ln2-.
(2)f′(x)=--1=-(x>0,m>0),
6
故当01时,f(x)在(0,)上单调递减,
在(,1)上单调递增.
14.(2020·江西赣州联考)已知函数f(x)=lnx,g(x)=ax+b.
(1)若f(x)与g(x)的图象在x=1处相切,求g(x)的表达式;
(2)若φ(x)=-f(x)在[1,+∞)上是减函数,求实数m的取值范围.
解:(1)由已知得f′(x)=,所以f′(1)=1=a,所以a=2.又因为g(1)=0=a+b,所以b=-1.所以g(x)=x-1.
(2)因为φ(x)=-f(x)=-lnx在[1,+∞)上是减函数,
所以φ′(x)=≤0在[1,+∞)上恒成立,
即x2-(2m-2)x+1≥0在[1,+∞)上恒成立,
则2m-2≤x+,x∈[1,+∞),
因为x+∈[2,+∞),所以2m-2≤2,即m≤2.
故实数m的取值范围是(-∞,2].
15.(2020·河南濮阳一模)已知f(x)=alnx+x2(a>0),若对任意两个不相等的正实数x1,x2,都有>2恒成立,则a的取值范围为( D )
A.(0,1] B.(1,+∞)
C.(0,1) D.[1,+∞)
解析:对任意两个不相等的正实数x1,x2,都有>2恒成立,则当x>0时,f′(x)≥2恒成立,f′(x)=+x≥2在(0,+∞)上恒成立,则a≥(2x-x2)max=1.故选D.
16.(2020·河南濮阳模拟)已知a=ln,b=e-1,c=,则a,b,c的大小关系为( D )
A.b>c>a B.a>c>b
C.a>b>c D.b>a>c
6
解析:依题意,得a=ln=,b=e-1=,c==.令f(x)=,则f′(x)=,易知函数f(x)在(0,e)上单调递增,在(e,+∞)上单调递减.所以f(x)max=f(e)==b,且f(3)>f(8),即a>c,所以b>a>c.故选D.
17.(2020·山东潍坊模拟)已知函数f(x)=(x-a)·ex-ax2+a(a-1)x(a∈R),讨论f(x)的单调性.
解:f′(x)=(x-a)ex+ex-ax+a(a-1)=[x-(a-1)](ex-a).
当a≤0时,ex-a>0.当x∈(-∞,a-1)时,f′(x)<0,f(x)为减函数;当x∈(a-1,+∞)时,f′(x)>0,f(x)为增函数.
当a>0时,令f′(x)=0,得x1=a-1,x2=lna.
令g(a)=a-1-lna,则g′(a)=1-=.
当a∈(0,1)时,g′(a)<0,g(a)为减函数;
当a∈(1,+∞)时,g′(a)>0,g(a)为增函数.
∴g(a)min=g(1)=0.
∴a-1≥lna(当且仅当a=1时取“=”).
∴当01时,x∈(-∞,lna),f′(x)>0,f(x)为增函数,x∈(lna,a-1),f′(x)<0,f(x)为减函数,x∈(a-1,+∞),f′(x)>0,f(x)为增函数.
当a=1时,f′(x)=x(ex-1)≥0,f(x)在(-∞,+∞)上为增函数.
综上所述,当a≤0时,f(x)在(-∞,a-1)上单调递减,在(a-1,+∞)上单调递增;
当01时,f(x)在(lna,a-1)上单调递减,在(-∞,lna)和(a-1,+∞)上单调递增;
当a=1时,f(x)在(-∞,+∞)上单调递增.
6