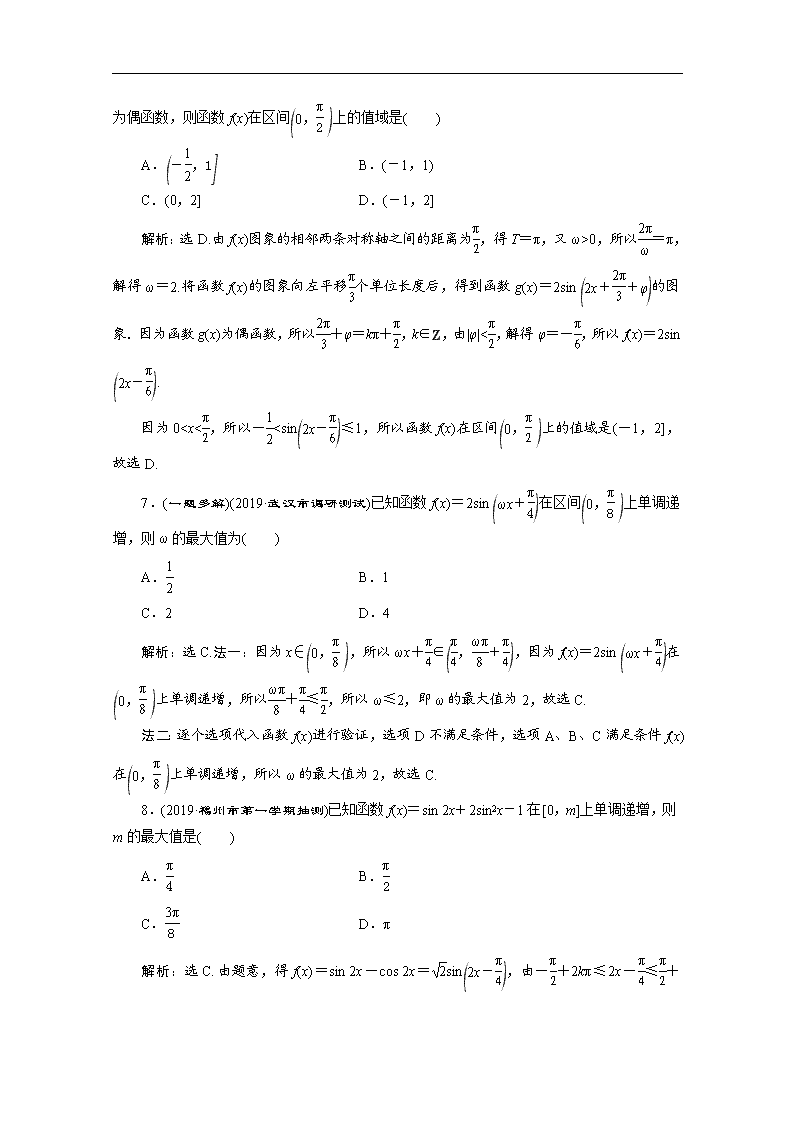2020高考数学二轮复习练习:第二部分 专题一 第1讲 三角函数的图象与性质 练典型习题 提数学素养含解析
一、选择题
1.(2019·高考全国卷Ⅱ)若 x1=π
4
,x2=3π
4
是函数 f(x)=sin ωx(ω>0)两个相邻的极值点,则
ω=( )
A.2 B.3
2
C.1 D.1
2
解析:选 A.依题意得函数 f(x)的最小正周期 T=2π
ω
=2×(3π
4
-π
4)=π,解得ω=2,选 A.
2.(2019·昆明市诊断测试)函数 y=sin 2x-π
3 图象的一条对称轴的方程为( )
A.x= π
12 B.x=π
6
C.x=π
3 D.x=5π
12
解析:选 D.由题意,令 2x-π
3
=π
2
+kπ(k∈Z),得对称轴方程为 x=5π
12
+kπ
2 (k∈Z),当 k=0
时,函数 y=sin 2x-π
3 图象的一条对称轴的方程为 x=5π
12.故选 D.
3.(2019·广东省七校联考)函数 f(x)=tan
x
2
-π
6 的单调递增区间是( )
A.2kπ-2π
3
,2kπ+4π
3 ,k∈Z
B.2kπ-2π
3
,2kπ+4π
3 ,k∈Z
C.4kπ-2π
3
,4kπ+4π
3 ,k∈Z
D. 4kπ-2π
3
,4kπ+4π
3 ,k∈Z
解析:选 B.由-π
2
+kπ
0,|φ|<π
2)的部分图象如图所示,
点 A(0, 3),B
π
6
,0 ,则函数 f(x)图象的一条对称轴为( )
A.x=-π
3 B.x=- π
12
C.x= π
18 D.x= π
24
解析:选 D.因为函数 f(x)=2cos(ωx+φ)的图象过点 A(0, 3),所以 2cos φ= 3,即 cos φ
= 3
2
,所以φ=2kπ±π
6(k∈Z).因为|φ|<π
2
,所以φ=±π
6
,由函数 f(x)的图象知φ
ω<0,又ω>0,所
以φ<0,所以φ=-π
6
,所以 f(x)=2cos(ωx-π
6).因为 f(x)=2cos(ωx-π
6)的图象过点 B
π
6
,0 ,所
以 cos(ω-1)π
6
=0,所以(ω-1)π
6
=mπ+π
2(m∈Z),所以ω=6m+4(m∈Z).因为ω>0,π
ω>π
6
,
所以 0<ω<6,所以ω=4,所以 f(x)=2cos 4x-π
6 .因为 x= π
24
时,f(x)=2,所以 x= π
24
为函数 f(x)
图象的一条对称轴,故选 D.
6.(2019·福州市质量检测)已知函数 f(x)=2sin(ωx+φ)(ω>0,|φ|<π
2)图象的相邻两条对称轴
之间的距离为π
2
,将函数 f(x)的图象向左平移π
3
个单位长度后,得到函数 g(x)的图象.若函数 g(x)
为偶函数,则函数 f(x)在区间 0,π
2 上的值域是( )
A. -1
2
,1 B.(-1,1)
C.(0,2] D.(-1,2]
解析:选 D.由 f(x)图象的相邻两条对称轴之间的距离为π
2
,得 T=π,又ω>0,所以2π
ω
=π,
解得ω=2.将函数 f(x)的图象向左平移π
3
个单位长度后,得到函数 g(x)=2sin 2x+2π
3
+φ 的图
象.因为函数 g(x)为偶函数,所以2π
3
+φ=kπ+π
2
,k∈Z,由|φ|<π
2
,解得φ=-π
6
,所以 f(x)=
2sin 2x-π
6 .
因为 0f
π
2 ,
则 f(x)取最大值时 x 的值为( )
A.π
3
+kπ,k∈Z B.π
4
+kπ,k∈Z
C.π
6
+kπ,k∈Z D.-π
6
+kπ,k∈Z
解析:选 C.由 f
π
3
-x =f(x)得 f(x)的图象关于直线 x=π
6
对称,即当 x=π
6
时,f(x)取得最值,
所以 2×π
6
+φ=nπ+π
2
,n∈Z,φ=nπ+π
6
,n∈Z.又 f(π)>f
π
2 ,所以 sin(2π+φ)>sin(π+φ),即
sin φ>-sin φ,得 sin φ>0,所以 n∈Z,且 n 为偶数.不妨取 n=0,即φ=π
6
,当 f(x)取最大值
时,2x+π
6
=2kπ+π
2
,k∈Z,解得 x=π
6
+kπ,k∈Z,故选 C.
10.(2019·广东六校第一次联考)已知 A 是函数 f(x)=sin 2 018x+π
6 +cos 2 018x-π
3 的最
大值,若存在实数 x1,x2 使得对任意实数 x,总有 f(x1)≤f(x)≤f(x2)成立,则 A|x1-x2|的最小值
为( )
A. π
2 018 B. π
1 009
C. 2π
1 009 D. π
4 036
解析:选 B.f(x)=sin 2 018x+π
6 +cos 2 018x-π
3 = 3
2 sin 2 018x+1
2cos 2 018x+1
2cos 2 018x
+ 3
2 sin 2 018x= 3sin 2 018x+cos 2 018x=2sin 2 018x+π
6 ,故 A=f(x)max=2,f(x)的最小正周
期 T= 2π
2 018
= π
1 009.又存在实数 x1,x2 使得对任意实数 x,总有 f(x1)≤f(x)≤f(x2)成立,所以 f(x2)
=f(x)max,f(x1)=f(x)min,故 A|x1-x2|的最小值为 A×1
2T= π
1 009
,故选 B.
11.(多选)已知函数 f(x)=sin4x-cos4x,则下列说法正确的是( )
A.f(x)的最小正周期为π
B.f(x)的最大值为 2
C.f(x)的图象关于 y 轴对称
D.f(x)在区间
π
4
,π
2 上单调递增
解析:选 ACD.因为 f(x)=sin4x-cos4x=sin2x-cos2x=-cos 2x,所以函数 f(x)的最小正周
期 T=π,f(x)的最大值为 1.
因为 f(-x)=-cos(-2x)=-cos 2x=f(x),所以 f(x)为偶函数,其图象关于 y 轴对称,因
为 y=cos 2x 在
π
4
,π
2 上单调递减,所以 f(x)=-cos 2x 在
π
4
,π
2 上单调递增,故选 ACD.
12.(多选)已知函数 f(x)=2sin(2x+φ)(0<φ<π),若将函数 f(x)的图象向右平移π
6
个单位长度
后,所得图象关于 y 轴对称,则下列结论中正确的是( )
A.φ=5π
6
B.
π
12
,0 是 f(x)图象的一个对称中心
C.f(φ)=-2
D.x=-π
6
是 f(x)图象的一条对称轴
解析:选 ABD.由题意得,平移后的函数 g(x)=f x-π
6 =2sin 2x-π
3
+φ 的图象关于 y 轴
对称,则-π
3
+φ=π
2
+kπ,k∈Z,因为 0<φ<π,所以φ=5π
6
,故 A 正确;f(x)=2sin 2x+5π
6 ,
由 2x+5π
6
=kπ,k∈Z,得对称中心的横坐标为-5π
12
+kπ
2
,k∈Z,故
π
12
,0 是 f(x)图象的一个
对称中心,故 B 正确;f(φ)=2sin
5π
3
+5π
6 =2sin 5π
2
=2,故 C 不正确;由 2x+5π
6
=π
2
+kπ,k
∈Z,得 x=-π
6
+kπ
2
,k∈Z,所以 x=-π
6
是 f(x)图象的一条对称轴,故 D 正确.
13.(多选)将函数 f(x)的图象向右平移π
6
个单位长度,再将所得函数图象上的所有点的横坐
标缩短到原来的2
3
,得到函数 g(x)=Asin(ωx+φ) A>0,ω>0,|φ|<π
2 的图象.已知函数 g(x)的部
分图象如图所示,则下列关于函数 f(x)的说法正确的是( )
A.f(x)的最小正周期为π,最大值为 2
B.f(x)的图象关于点
π
6
,0 中心对称
C.f(x)的图象关于直线 x=π
6
对称
D.f(x)在区间
π
6
,π
3 上单调递减
解析:选 ACD.由图可知,A=2,T=4×
2π
9
- π
18 =2π
3
,所以ω=2π
T
=3.
又由 g
2π
9 =2 可得φ=-π
6
+2kπ(k∈Z),且|φ|<π
2
,所以φ=-π
6.
所以 g(x)=2sin 3x-π
6 ,
所以 f(x)=2sin 2x+π
6 .
所以 f(x)的最小正周期为π,最大值为 2,选项 A 正确.
对于选项 B,令 2x+π
6
=k′π(k′∈Z),得 x=k′π
2
- π
12(k′∈Z),所以函数 f(x)图象的对称中心
为
k′π
2
- π
12
,0 (k′∈Z),由k′π
2
- π
12
=π
6
,
得 k′=1
2
,不符合 k′∈Z,B 错误.
对于选项 C,令 2x+π
6
=π
2
+kπ(k∈Z),得 x=π
6
+kπ
2 (k∈Z),所以函数 f(x)图象的对称轴为
直线 x=π
6
+kπ
2 (k∈Z),当 k=0 时,x=π
6
,故 C 正确.
当 x∈[π
6
,π
3]时,2x+π
6
∈
π
2
,5π
6 ,所以 f(x)在区间
π
6
,π
3 上单调递减,所以选项 D 正确.故
选 ACD.
二、填空题
14.已知函数 f(x)=4cos(ωx+φ)(ω>0,0<φ<π)为奇函数,A(a,0),B(b,0)是其图象上两
点,若|a-b|的最小值是 1,则 f
1
6 =________.
解析:因为函数 f(x)=4cos(ωx+φ)(ω>0,0<φ<π)为奇函数,所以 cos φ=0(0<φ<π),所以φ
=π
2
,所以 f(x)=-4sin ωx,又 A(a,0),B(b,0)是其图象上两点,且|a-b|的最小值是 1,所
以函数 f(x)的最小正周期为 2,所以ω=π,所以 f(x)=-4sin πx,所以 f
1
6 =-4sin π
6
=-2.
答案:-2
15.(2019·长春市质量监测(二))定义在[0,π]上的函数 y=sin ωx-π
6 (ω>0)有零点,且值
域 M⊆ -1
2
,+∞ ,则ω的取值范围是________.
解析:由 0≤x≤π,得-π
6
≤ωx-π
6
≤ωπ-π
6
,当 x=0 时,y=-1
2.因为函数 y=sin ωx-π
6
在[0,π]上有零点,所以 0≤ωπ-π
6
,ω≥1
6.因为值域 M⊆ -1
2
,+∞ ,所以ωπ-π
6
≤π+π
6
,ω
≤4
3
,从而1
6
≤ω≤4
3.
答案:
1
6
,4
3
16.(2019·蓉城名校第一次联考)已知关于 x 的方程 2sin2x- 3sin 2x+m-1=0 在
π
2
,π 上
有两个不同的实数根,则 m 的取值范围是________.
解析:因为 2sin2x- 3sin 2x+m-1=0,
所以 1-cos 2x- 3sin 2x+m-1=0,
所以 cos 2x+ 3sin 2x-m=0,
所以 2sin 2x+π
6 =m,即 sin 2x+π
6 =m
2.
方程 2sin2x- 3sin 2x+m-1=0 在
π
2
,π 上有两个不同的实数根,即 y=sin 2x+π
6 ,x∈
π
2
,π 的图象与 y=m
2
的图象有 2 个不同的交点.作出 y=sin 2x+π
6 ,x∈
π
2
,π 及 y=m
2
的图
象如图所示,则-10,x∈R,且 f(α)=-1
2
,
f(β)=1
2.若|α-β|的最小值为3π
4
,则 f
3π
4 =________,函数 f(x)的单调递增区间为________.
解析:函数 f(x)=sin ωx-π
6 +1
2
,ω>0,x∈R,由 f(α)=-1
2
,f(β)=1
2
,且|α-β|的最小值
为3π
4
,得T
4
=3π
4
,即 T=3π=2π
ω
,所以ω=2
3.所以 f(x)=sin
2
3x-π
6 +1
2.则 f
3π
4 =sin π
3
+1
2
= 3+1
2 .
由-π
2
+2kπ≤2
3x-π
6
≤π
2
+2kπ,k∈Z,得-π
2
+3kπ≤x≤π+3kπ,k∈Z,即函数 f(x)的单调递增
区间为 -π
2
+3kπ,π+3kπ ,k∈Z.
答案: 3+1
2
-π
2
+3kπ,π+3kπ ,k∈Z