- 2021-06-09 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届高考一轮复习北师大版理4-4简单的三角恒等变换学案
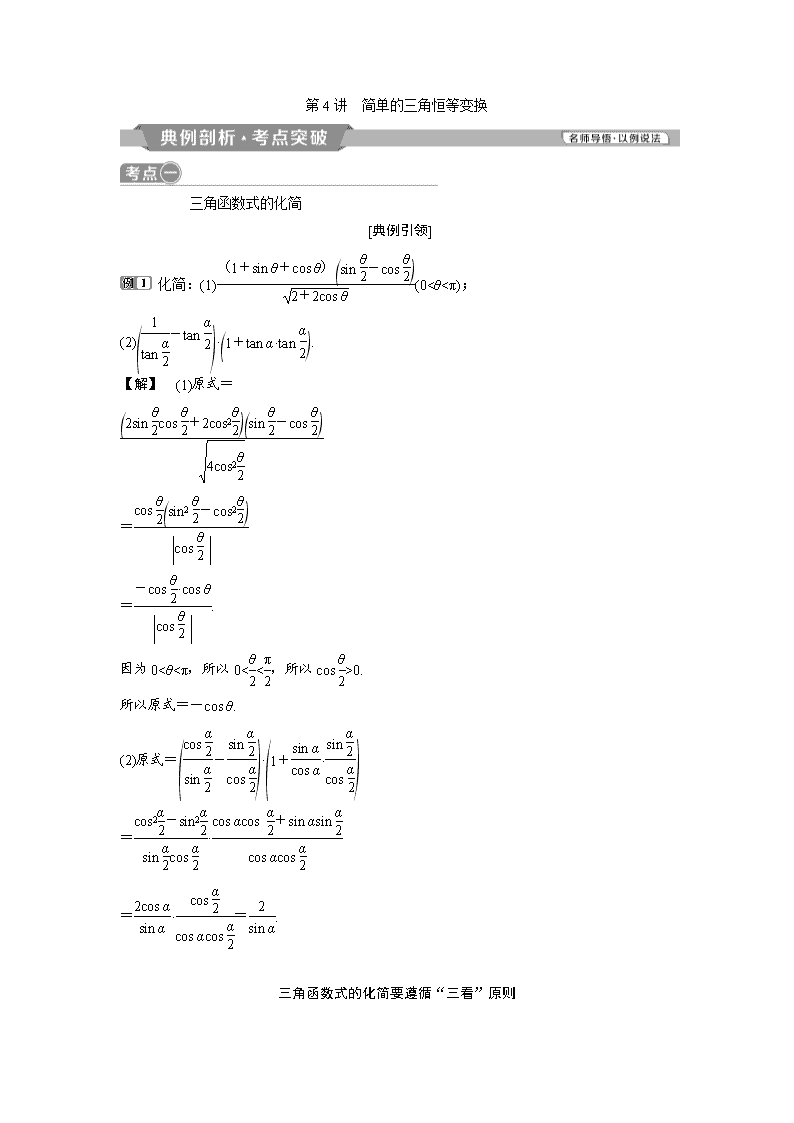
第4讲 简单的三角恒等变换 三角函数式的化简 [典例引领] 化简:(1)(0<θ<π); (2)·. 【解】 (1)原式= = =. 因为0<θ<π,所以0<<,所以cos >0. 所以原式=-cos θ. (2)原式=· =· =·=. 三角函数式的化简要遵循“三看”原则 [通关练习] 1.(2018·长沙模拟)化简:=________. 解析:== =4sin α. 答案:4sin α 2.化简:. 解:原式= = = =cos 2x. 三角函数式的求值(高频考点) 三角函数式的求值在高考中主要以选择题形式出现,有时以解答题某一步出现,试题难度较小.高考对三角函数求值的考查有以下三个命题角度: (1)给角求值; (2)给值求值; (3)给值求角. [典例引领] 角度一 给角求值 的值是________. 【解析】 = ===2. 【答案】 2 角度二 给值求值 已知α∈,且2sin2α-sin αcos α-3cos2 α=0,求的值. 【解】 因为α∈,且2sin2α-sin αcos α-3cos2α=0,则(2sin α-3cos α)(sin α+cos α)=0, 所以2sin α=3cos α,又sin2α+cos2α=1, 所以cos α=,sin α=, 所以 ==. 角度三 给值求角 已知tan α,tan β是方程x2+3x+4=0的两根,且α,β∈,则α+β=( ) A. B.或- C.-或 D.- 【解析】 由题意得tan α+tan β=-3<0,tan αtan β=4>0,所以tan(α+β)==,且tan α<0,tan β<0,又由α,β∈得α,β∈,所以α+β∈(-π,0),所以α+β =-. 【答案】 D 三角函数求值的3种情况 [通关练习] 1.计算:=( ) A. B.- C. D.- 解析:选D.原式=-·=-tan=-×=-. 2.已知sin α=且α为第二象限角,则tan=( ) A.- B.- C.- D.- 解析:选D.由题意得cos α=-,则sin 2α=-,cos 2α=2cos2α-1=,所以tan 2α=-,所以tan===-. 3.(2018·南充模拟)已知α∈,β∈,且cos α=,cos(α+β)=-,则β=________. 解析:因为α∈,β∈,且cos α=,cos=-, 所以sin α==, sin(α+β)==, 则sin β=sin[(α+β)-α] =sin(α+β)cos α-cos(α+β)sin α =×-×=,因为β∈,所以β=. 答案: 三角恒等变换的简单应用 [典例引领] 如图,现要在一块半径为1 m,圆心角为的扇形白铁片AOB上剪出一个平行四边形MNPQ,使点P在弧AB上,点Q在OA上,点M,N在OB上,设∠BOP=θ,平行四边形MNPQ的面积为S. (1)求S关于θ的函数关系式; (2)求S的最大值及相应的θ角. 【解】 (1)分别过P,Q作PD⊥OB于点D,QE⊥OB于点E,则四边形QEDP为矩形. 由扇形半径为1 m,得PD=sin θ,OD=cos θ. 在Rt△OEQ中, OE=QE=PD, MN=QP=DE=OD-OE=cos θ-sin θ, S=MN·PD=·sin θ =sin θcos θ-sin2θ,θ∈. (2)S=sin 2θ-(1-cos 2θ) =sin 2θ+cos 2θ-=sin-, 因为θ∈, 所以2θ+∈,sin∈. 当θ=时,Smax=(m2). 利用三角恒等变换解决实际问题的思路 (1)结合具体图形引进角为参数,利用三角函数的有关公式进行化简,解决最优化问题. (2)解决三角函数应用问题和解决一般应用性问题一样,先建模,再讨论变量的范围,最后作出结论并回答问题. [提醒] 注意恰当选择自变量,并利用解直角三角形等知识表示有关线段. 如图,有一块以点O为圆心的半圆形空地,要在这块空地上划出一个内接矩形ABCD开辟为绿地,使其一边AD落在半圆的直径上,另两点B,C落在半圆的圆周上.已知半圆的半径长为20 m,如何选择关于点O对称的点A,D的位置,可以使矩形ABCD的面积最大,最大值是多少? 解:连接OB,设∠AOB=θ, 则AB=OBsin θ=20sin θ,OA=OBcos θ=20cos θ,且θ∈. 因为A,D关于原点对称, 所以AD=2OA=40cos θ. 设矩形ABCD的面积为S,则 S=AD·AB=40cos θ·20sin θ =400sin 2θ.因为θ∈, 所以当sin 2θ=1, 即θ=时,Smax=400(m2). 此时AO=DO=10(m). 故当A、D距离圆心O为10 m时,矩形ABCD的面积最大,其最大面积是400 m2. 三角恒等变换三大原则 (1)变角:目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”. (2)变名:通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”“升幂与降幂”等. (3)变式:根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有“常值代换”“正用、逆用公式”“通分与约分”“分解与组合”“配方与平方”等. 易错防范 在求角的某个三角函数值时,应注意根据条件选择恰当的函数,尽量做到所选函数在确定角的范围内为一对一函数. (1)已知正切函数值,选正切函数; (2)已知正、余弦函数值,选正弦或余弦函数;若角的范围是,选正、余弦函数皆可;若角的范围是(0,π),选余弦函数较好;若角的范围为,选正弦函数较好. 1.已知sin 2α=,则cos2=( ) A. B.- C. D.- 解析:选C.cos2====,故选C. 2.已知f(x)=2tan x-,则f的值为( ) A.4 B. C.4 D.8 解析:选D.因为f(x)=2=2×=2×=, 所以f==8. 3.(2018·湖北新联考模拟)=( ) A. B. C. D.1 解析:选A.====.故选A. 4.已知α,β均为锐角,(1+tanα)(1+tan β)=2,则α+β为( ) A. B. C. D. 解析:选B.由(1+tan α)(1+tan β)=2得 tan α+tan β=1-tan αtan β, 所以tan(α+β)===1. 因为0<α,β<,所以0<α+β<π,所以α+β=. 5.sin220°+cos280°+sin 20°cos 80°的值为( ) A. B. C. D.1 解析:选A.sin220°+cos280°+sin 20°·cos 80° =(1-cos 40°)+(1+cos 160°)+sin 20°cos(60°+20°) =1-cos 40°+(cos 120°·cos 40°-sin 120°·sin 40°)+sin 20°(cos 60°cos 20°-sin 60°sin 20°) =1-cos 40°-cos 40°-sin 40°+sin 40°-sin220° =1-cos 40°-(1-cos 40°)=. 6.-=________. 解析:原式= ==tan 30°=. 答案: 7.已知cos 2θ=,则sin4θ+cos4θ=________. 解析:法一:因为cos 2θ=, 所以2cos2θ-1=,1-2sin2θ=, 因为cos2θ=,sin2θ=, 所以sin4θ+cos4θ=. 法二:sin4θ+cos4θ=(sin2θ+cos2θ)2-sin22θ =1-(1-cos22θ)=1-×=. 答案: 8.已知=,tan(α-β)=,则tan β=________. 解析:因为=,所以=,=1,所以tan α=1,又因为tan(α-β)=, 所以tan β=tan[α-(α-β)]===. 答案: 9.化简:. 解: == === ==tan α. 10.已知tan α=-,cos β=,α∈,β∈,求tan(α+β)的值,并求出α+β的值. 解:由cos β=,β∈, 得sin β=,tan β=2. 所以tan(α+β)= ==1. 因为α∈,β∈, 所以<α+β<, 所以α+β=. 1.若sin 2α=,sin(β-α)=,且α∈,β∈,则α+β的值是( ) A. B. C.或 D.或 解析:选A.因为sin 2α=,α∈,所以cos 2α=-且α∈,又因为sin(β-α)=,β∈, 所以cos(β-α)=-,因此cos(α+β)=cos[(β-α)+2α]=cos(β-α)·cos 2α-sin(β-α)sin 2α=-×-×=,又α+β∈,所以α+β=,故选A. 2.(2018·山西省晋中名校高三联合测试)对于集合{a1,a2,…,an}和常数a0,定义:ω= 为集合{a1,a2,…,an}相对a0的“正弦方差”,则集合相对a0的“正弦方差”为( ) A. B. C. D.与a0有关的一个值 解析:选A.集合相对a0的“正弦方差” ω= = = = = =. 3.(2018·云南省第一次统一检测)计算 =________(用数字作答). 解析:====. 答案: 4.(2018·济南模拟)设α∈,β∈,且5sin α+5cos α=8,sin β+cos β=2,则cos(α+β)的值为________. 解析:由5sin α+5cos α=8,得sin=, 因为α∈,α+∈, 所以cos=. 又β∈,β+∈, 由sin β+cos β=2,得 sin=. 所以cos=-. 所以cos(α+β)=sin =sin =sincos+cossin =-. 答案:- 5.已知函数f(x)=Acos(+),x∈R,且f=. (1)求A的值; (2)设α,β∈,f=-,f=,求cos(α+β)的值. 解:(1)因为f=Acos=Acos=A=, 所以A=2. (2)由f=2cos(α++)=2cos=-2sin α=-, 得sin α=,又α∈, 所以cos α=. 由f=2cos(β-+) =2cos β=, 得cos β=,又β∈, 所以sin β=, 所以cos(α+β)=cos αcos β-sin αsin β =×-×=-. 6.广告公司为某游乐场设计某项设施的宣传画,根据该设施的外观,设计成的平面图由半径为2 m的扇形AOB和三角区域BCO构成,其中C,O,A在一条直线上,∠ACB=, 记该设施平面图的面积为S(x)m2,∠AOB=x rad,其中查看更多
相关文章
- 当前文档收益归属上传用户