【物理】2019届一轮复习人教版电磁感应规律的综合应用(二)——动力学和能量、动量学案

【物理】2019届一轮复习人教版电磁感应规律的综合应用(二)——动力学和能量、动量学案

第4讲电磁感应规律的综合应用(二)——动力学和能量、动量 板块一　主干梳理·夯实基础 ‎【知识点1】　电磁感应现象中的动力学问题　Ⅱ ‎1．安培力的大小 ‎2．安培力的方向 ‎(1)先用右手定则或楞次定律确定感应电流方向，再用左手定则确定安培力方向。‎ ‎(2)根据楞次定律，安培力方向一定和导体切割磁感线运动方向相反。‎ ‎3．分析导体受力情况时，应做包含安培力在内的全面受力分析。‎ ‎4．根据平衡条件或牛顿第二定律列方程。‎ ‎【知识点2】　电磁感应现象中的能量问题　Ⅱ ‎1．电磁感应中的能量转化 闭合电路的部分导体做切割磁感线运动产生感应电流，通有感应电流的导体在磁场中受安培力。外力克服安培力做功，将其他形式的能转化为电能，通有感应电流的导体在磁场中受安培力作用或通过电阻发热，使电能转化为其他形式的能。‎ ‎2．实质 电磁感应现象的能量转化，实质是其他形式的能和电能之间的转化。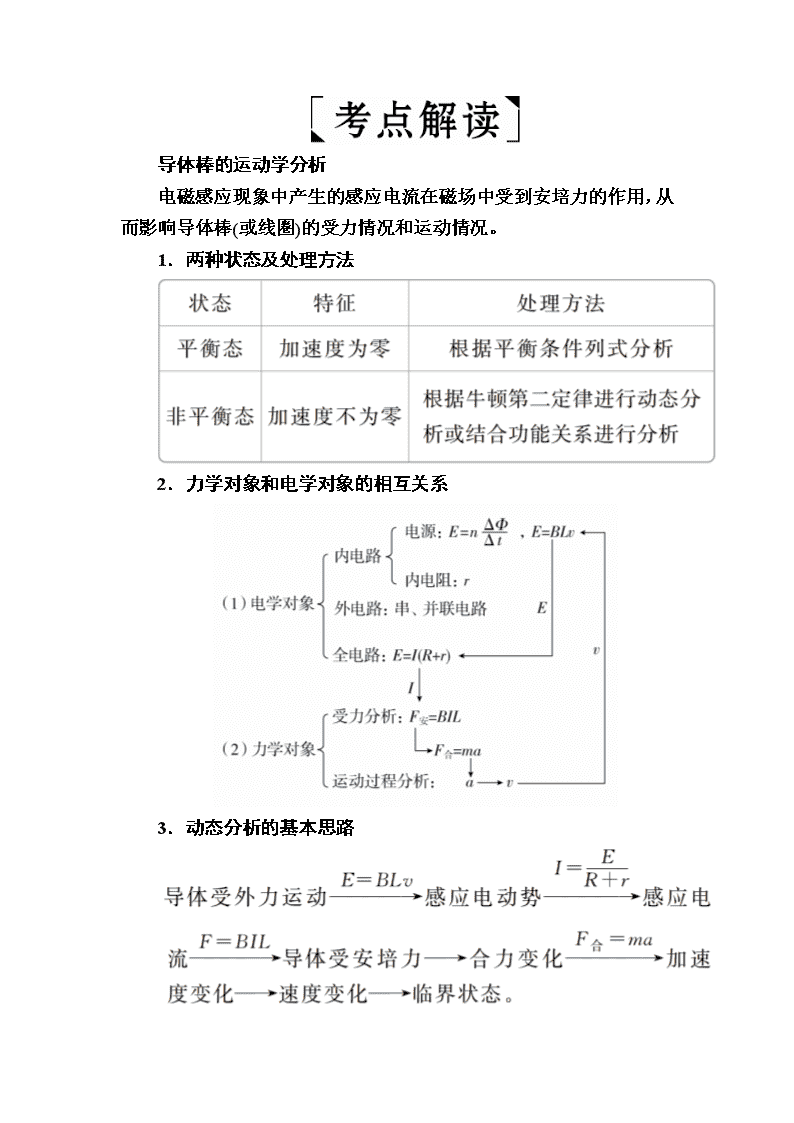‎ 板块二　考点细研·悟法培优 考点1 电磁感应中的动力学问题 [解题技巧]‎ 导体棒的运动学分析 电磁感应现象中产生的感应电流在磁场中受到安培力的作用，从而影响导体棒(或线圈)的受力情况和运动情况。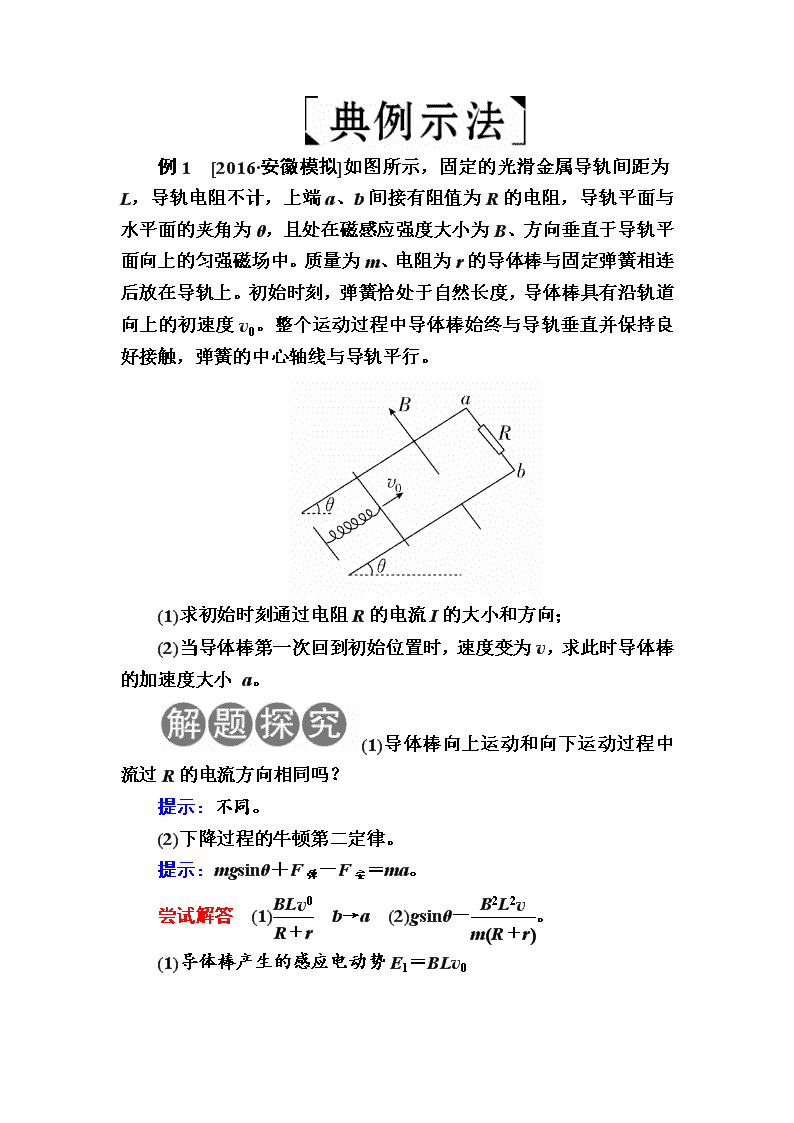‎ ‎1．两种状态及处理方法 ‎2．力学对象和电学对象的相互关系 ‎3．动态分析的基本思路 例1　[2016·安徽模拟]如图所示，固定的光滑金属导轨间距为L，导轨电阻不计，上端a、b间接有阻值为R的电阻，导轨平面与水平面的夹角为θ，且处在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中。质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上。初始时刻，弹簧恰处于自然长度，导体棒具有沿轨道向上的初速度v0。整个运动过程中导体棒始终与导轨垂直并保持良好接触，弹簧的中心轴线与导轨平行。‎ ‎(1)求初始时刻通过电阻R的电流I的大小和方向；‎ ‎(2)当导体棒第一次回到初始位置时，速度变为v，求此时导体棒的加速度大小 a。‎ ‎(1)导体棒向上运动和向下运动过程中流过R的电流方向相同吗？‎ 提示：不同。‎ ‎(2)下降过程的牛顿第二定律。‎ 提示：mgsinθ＋F弹－F安＝ma。‎ 尝试解答　(1)　b→a　(2)gsinθ－。‎ ‎(1)导体棒产生的感应电动势E1＝BLv0‎ 通过R的电流大小I1＝＝ 电流方向为b→a。‎ ‎(2)导体棒产生的感应电动势为E2＝BLv 感应电流I2＝＝ 导体棒受到的安培力大小F＝BIL＝，方向沿斜面向上。‎ 根据牛顿第二定律有mgsinθ－F＝ma 解得a＝gsinθ－。‎ 总结升华 单棒切割磁感线的两种模型 模型一：导体棒ab先自由下落再进入匀强磁场，如图甲所示。‎ 模型二：导体棒ab沿光滑的倾斜导轨自由下滑，然后进入匀强磁场(磁场垂直于轨道平面)，如图乙所示。‎ 两类模型中的临界条件是导体棒ab受力平衡。以模型一为例，有mg＝F安＝，即v0＝。‎ 若线框进入磁场时v>v0，则线框先减速再匀速；若v0，则金属棒做加速度增大的加速运动，其vt图象如图甲所示；由i＝可知感应电流i与v成正比，则it图线应该和vt图线形状相同；由FA＝得FA与v成正比，图象应该与vt图象形状相同，B正确；UR＝IR＝知UR与v成正比，图象应该与vt图象形状相同；由P＝＝得P与v2成正比，Pt图象应该是曲线。若k－<0，则金属棒做加速度减小的加速运动，其vt图象如图乙所示；由i＝可知感应电流i与v成正比，则it图线应该和vt图线形状相同，A错误；FA＝得FA与v成正比，图象应该与vt图象形状相同；由UR＝IR＝知UR 与v成正比，图象应该与vt图象形状相同，C正确；由P＝＝得P与v2成正比，Pt图象也应该是曲线，D错误；同理可知当k－＝0时A、D亦错误。故选B、C。‎ 二、非选择题 ‎10．[2017·江苏高考]如图所示，两条相距d的平行金属导轨位于同一水平面内，其右端接一阻值为R的电阻。质量为m的金属杆静置在导轨上，其左侧的矩形匀强磁场区域MNPQ的磁感应强度大小为B、方向竖直向下。当该磁场区域以速度v0匀速地向右扫过金属杆后，金属杆的速度变为v。导轨和金属杆的电阻不计，导轨光滑且足够长，杆在运动过程中始终与导轨垂直且两端与导轨保持良好接触。求：‎ ‎(1)MN刚扫过金属杆时，杆中感应电流的大小I；‎ ‎(2)MN刚扫过金属杆时，杆的加速度大小a；‎ ‎(3)PQ刚要离开金属杆时，感应电流的功率P。‎ 答案　(1)　(2)　(3) 解析　(1)MN刚扫过金属杆时，金属杆的感应电动势E＝Bdv0①‎ 回路的感应电流I＝②‎ 由①②式解得I＝③‎ ‎(2)金属杆所受的安培力F＝BId④‎ 由牛顿第二定律得，对金属杆F＝ma⑤‎ 由③④⑤式得a＝⑥‎ ‎(3)金属杆切割磁感线的相对速度v′＝v0－v⑦‎ 感应电动势E′＝Bdv′⑧‎ 感应电流的电功率P＝⑨‎ 由⑦⑧⑨式得P＝。‎ ‎11．[2017·天津高考]电磁轨道炮利用电流和磁场的作用使炮弹获得超高速度，其原理可用来研制新武器和航天运载器。电磁轨道炮示意如图，图中直流电源电动势为E，电容器的电容为C。两根固定于水平面内的光滑平行金属导轨间距离为l，电阻不计。炮弹可视为一质量为m、电阻为R的金属棒MN，垂直放在两导轨间处于静止状态，并与导轨良好接触。首先开关S接1，使电容器完全充电。然后将S接至2，导轨间存在垂直于导轨平面、磁感应强度大小为B的匀强磁场(图中未画出)，MN开始向右加速运动。当MN上的感应电动势与电容器两极板间的电压相等时，回路中电流为零，MN达到最大速度，之后离开导轨。问：‎ ‎(1)磁场的方向；‎ ‎(2)MN刚开始运动时加速度a的大小；‎ ‎(3)MN离开导轨后电容器上剩余的电荷量Q是多少。‎ 答案　(1)垂直于导轨平面向下　(2) ‎(3) 解析　(1)将S接1时，电容器充电，上极板带正电，下极板带负电，当将S接2时，电容器放电，流经MN的电流由M到N，又知MN向右运动，由左手定则可知磁场方向垂直于导轨平面向下。‎ ‎(2)电容器完全充电后，两极板间电压为E，当开关S接2时，电容器放电，设刚放电时流经MN的电流为I，有 I＝①‎ 设MN受到的安培力为F，有 F＝IlB②‎ 由牛顿第二定律，有 F＝ma③‎ 联立①②③式得 a＝④‎ ‎(3)当电容器充电完毕时，设电容器上电荷量为Q0，有 Q0＝CE⑤‎ 开关S接2后，MN开始向右加速运动，速度达到最大值vmax时，设MN上的感应电动势为E′，有 E′＝Blvmax⑥‎ 依题意有 E′＝⑦‎ 设在此过程中MN的平均电流为，MN上受到的平均安培力为，有 ＝lB⑧‎ 由动量定理，有 Δt＝mvmax－0⑨‎ 又Δt＝Q0－Q⑩‎ 联立⑤⑥⑦⑧⑨⑩式得 Q＝。‎ ‎12. [2016·全国卷Ⅰ]如图，两固定的绝缘斜面倾角均为θ，上沿相连。两细金属棒ab(仅标出a端)和cd(仅标出c端)长度均为L，质量分别为‎2m和m；用两根不可伸长的柔软轻导线将它们连成闭合回路abdca，并通过固定在斜面上沿的两光滑绝缘小定滑轮跨放在斜面上，使两金属棒水平。右斜面上存在匀强磁场，磁感应强度大小为B，方向垂直于斜面向上。已知两根导线刚好不在磁场中，回路电阻为R，两金属棒与斜面间的动摩擦因数均为μ，重力加速度大小为g。已知金属棒ab匀速下滑。求：‎ ‎(1)作用在金属棒ab上的安培力的大小；‎ ‎(2)金属棒运动速度的大小。‎ 答案　(1)mg(sinθ－3μcosθ)　(2) 解析　(1)设导线的张力的大小为T，右斜面对ab棒的支持力的大小为N1，作用在ab棒上的安培力的大小为F，左斜面对cd棒的 支持力大小为N2。‎ 对于ab棒，由力的平衡条件得 ‎2mgsinθ＝μN1＋2T＋F①‎ N1＝2mgcosθ②‎ 对于cd棒，同理有 mgsinθ＋μN2＝2T③‎ N2＝mgcosθ④‎ 联立①②③④式得 F＝mg(sinθ－3μcosθ)⑤‎ ‎(2)由安培力公式得 F＝BIL⑥‎ 这里I是回路abdca中的感应电流。ab棒上的感应电动势为 E＝BLv⑦‎ 式中，v是ab棒下滑速度的大小。由欧姆定律得 I＝⑧‎ 联立⑤⑥⑦⑧式得 v＝。‎