高二物理同步训练：2

高二物理同步训练：2

高二物理同步训练试题解析一、选择题1．关于电动势，以下说法中正确的是(　　)A．电源电动势等于电源正、负极之间的电势差B．用电压表直接测量电源两极得到的电压数值，实际上总略小于电源电动势的准确值C．电源电动势总等于内、外电路上的电压之和，所以它的数值与外电路的组成有关D．在闭合电路中，当外电阻变大时，路端电压增大，电源的电动势也增大解析：选B.电动势是电源本身的属性，是由电源本身决定的，与外电路的组成及变化无关，故C、D错误．由闭合电路的欧姆定律得E＝U＋Ir.用电压表直接测量电源两极时，虽然电压表的电阻很大，但电路中也有电流，内电路中也有电压降落，电压表直接测量电源两极得到的电压数值应略小于电动势，B正确，A错误．2．当外电路的电阻分别为8Ω和2Ω时，单位时间内在外电路上产生的热量正好相等，则该电源的内电阻是(　　)A．1Ω　　　　　　　B．2ΩC．4ΩD．6Ω解析：选C.由()2R1＝()2R2，代入数据解得r＝4Ω，选项C正确．3．如图2－7－17所示为闭合电路中两个不同电源的U－I图象，则下列说法中正确的是(　　)图2－7－17A．电动势E1＝E2，短路电流I1>I2B．电动势E1＝E2，内阻r1>r2C．电动势E1>E2，内阻r1>r2D．当两电源的工作电流变化量相同时，电源2的路端电压变化较大解析：选AD.由闭合电路的欧姆定律得E＝U＋Ir.当I＝0时电动势E等于路端电压U，即U－I图线和U轴的交点就是电动势，由图知，两电源的电动势相等．当U＝0时I＝E/r，U－I图线和I轴的交点就是短路电流，由图知I1>I2.A正确．而r＝E/I，即图线的斜率表示电源的内阻，由图知r1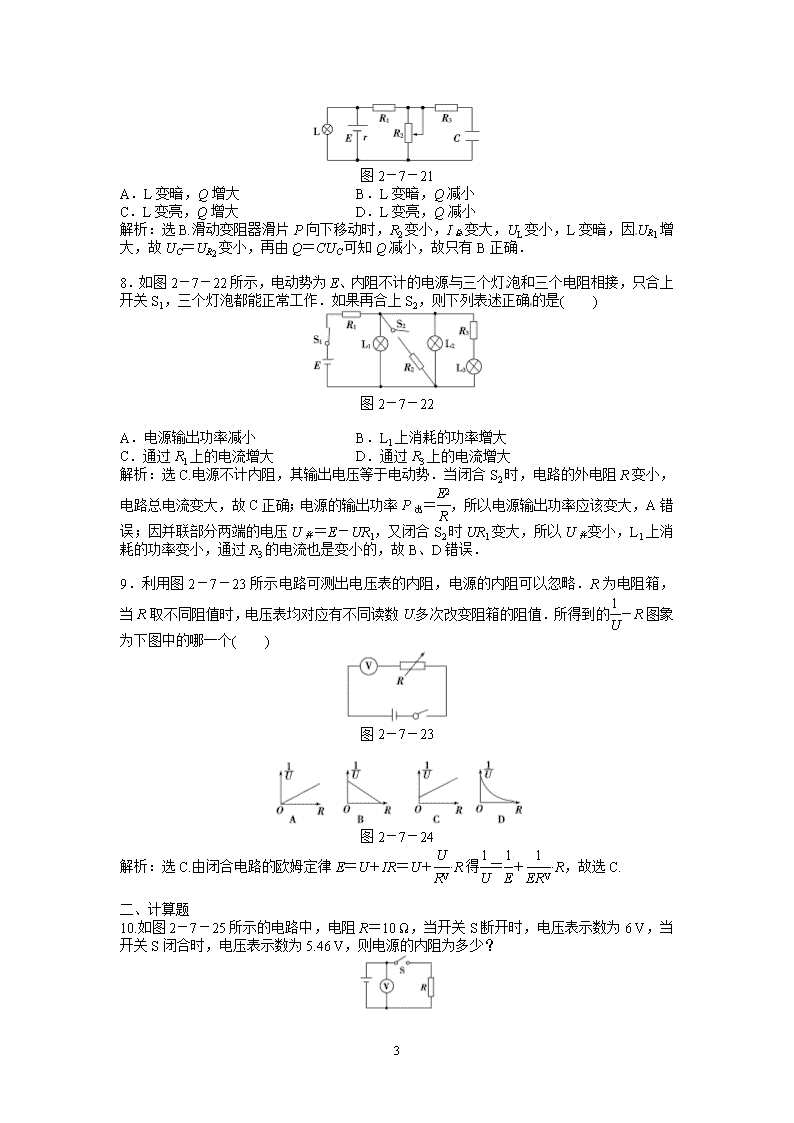P2B．P1η2D．η1<η2解析：选C.由直线A可知，E＝6V，r＝1Ω，由直线B、C可知，R1＝2Ω，R2＝0.5Ω，P1＝()2·R1＝8W，η1＝＝，P2＝()2R2＝8W，η2＝＝故有：P1＝P2　η1>η2，只有C正确．5．在图2－7－19所示的电路中，电源电动势为E、内电阻为r.在滑动变阻器的滑动触片P从图示位置向上滑动的过程中(　　)图2－7－19A．电路中的总电流变大B．路端电压变大C．通过电阻R2的电流变大D．通过滑动变阻器R1的电流变小解析：选BCD.本题可按照以下思路分析：　　　　　　　　　　　　　　　　　　　故B、C、D均正确．6．图2－7－20所示是一实验电路图．在滑动触头由a端滑向b端的过程中，下列表述正确的是(　　)图2－7－20A．路端电压变小B．电流表的示数变大C．电源内阻消耗的功率变小D．电路的总电阻变大解析：选A.由a到b，R1电阻值减小，因此总电阻变小，D错，总电流增大，内电压增大，路端电压减小，所以A正确．再结合欧姆定律知电流表的示数变小，B错，由P内＝I2r知电源内阻消耗的功率变大，C错．7．在如图2－7－21所示的电路中，当滑动变阻器的滑动片向下移动时，关于电灯L的亮度及电容器C所带电荷量Q的变化判断正确的是(　　)5 图2－7－21A．L变暗，Q增大B．L变暗，Q减小C．L变亮，Q增大D．L变亮，Q减小解析：选B.滑动变阻器滑片P向下移动时，R2变小，I总变大，UL变小，L变暗，因UR1增大，故UC＝UR2变小，再由Q＝CUC可知Q减小，故只有B正确．8．如图2－7－22所示，电动势为E、内阻不计的电源与三个灯泡和三个电阻相接，只合上开关S1，三个灯泡都能正常工作．如果再合上S2，则下列表述正确的是(　　)图2－7－22A．电源输出功率减小　　　B．L1上消耗的功率增大C．通过R1上的电流增大D．通过R3上的电流增大解析：选C.电源不计内阻，其输出电压等于电动势．当闭合S2时，电路的外电阻R变小，电路总电流变大，故C正确；电源的输出功率P出＝，所以电源输出功率应该变大，A错误；因并联部分两端的电压U并＝E－UR1，又闭合S2时UR1变大，所以U并变小，L1上消耗的功率变小，通过R3的电流也是变小的，故B、D错误．9．利用图2－7－23所示电路可测出电压表的内阻，电源的内阻可以忽略．R为电阻箱，当R取不同阻值时，电压表均对应有不同读数U.多次改变阻箱的阻值．所得到的－R图象为下图中的哪一个(　　)图2－7－23图2－7－24解析：选C.由闭合电路的欧姆定律E＝U＋IR＝U＋·R得＝＋·R，故选C.二、计算题10.如图2－7－25所示的电路中，电阻R＝10Ω，当开关S断开时，电压表示数为6V，当开关S闭合时，电压表示数为5.46V，则电源的内阻为多少？5 图2－7－25解析：当开关S断开时，R外→∞，所以E＝U外＝6V.当开关S闭合时，U外＝IR，即5.46V＝I×10Ω，所以I＝0.546A，又由E＝U外＋Ir，即6V＝5.46V＋0.546r，解得r≈1Ω.答案：1Ω11.如图2－7－26所示，E＝10V，r＝1Ω，R1＝R3＝5Ω，R2＝4Ω，C＝100μF.当S断开时，电容器中带电粒子恰好处于静止状态．求：图2－7－26(1)S闭合后，带电粒子加速度的大小和方向；(2)S闭合后流过R3的总电荷量．解析：(1)开始带电粒子恰好处于静止状态，必有qE＝mg且qE竖直向上．S闭合后，qE＝mg的平衡关系被打破．S断开，带电粒子恰好处于静止状态，设电容器两极板间距离为d，有UC＝E＝4V，qUC/d＝mg.S闭合后，U′C＝E＝8V设带电粒子加速度为a，则qU′C/d－mg＝ma，解得a＝g，方向竖直向上．(2)S闭合后，流过R3的总电荷量等于电容器上电荷的增加量，所以ΔQ＝C(U′C－UC)＝4×10－4C.答案：(1)g方向向上　(2)4×10－4C12．在图2－7－27甲所示电路中，R1、R2均为定值电阻，且R1＝100Ω，R2的阻值未知，R3是一滑动变阻器，当其滑片从最左端滑至最右端的过程中，测得电源的路端电压U随电流I的变化图线如图乙所示，其中图线上的A、B两点是滑片在变阻器上的两个不同端点时分别得到的．求：甲　　　　　　　　　　乙图2－7－27(1)电源的电动势和内电阻；(2)定值电阻R2的阻值；(3)滑动变阻器R3的最大值．解析：(1)由闭合电路欧姆定律得：E＝U＋Ir将图象中A、B两点的电压和电流代入得：5 E＝16＋0.2r　E＝4＋0.8r解得E＝20V，r＝20Ω.(2)当R3的滑片滑到最右端时，R3、R1均被短路，此时外电路电阻等于R2，且对应于图线上B点，故由B点的U、I值可求出R2的阻值为：R2＝＝Ω＝5Ω.(3)滑动变阻器的滑片置于最左端时，R3阻值最大．设此时外电路总电阻为R，由图象中A点坐标求出：R＝＝Ω＝80Ω.又R＝＋R2，代入数值解得滑动变阻器的最大阻值R3＝300Ω.答案：(1)20V　20Ω　(2)5Ω　(3)300Ω。5