高考一模北京西城北京市西城区高三一模数学理科试题版含答案

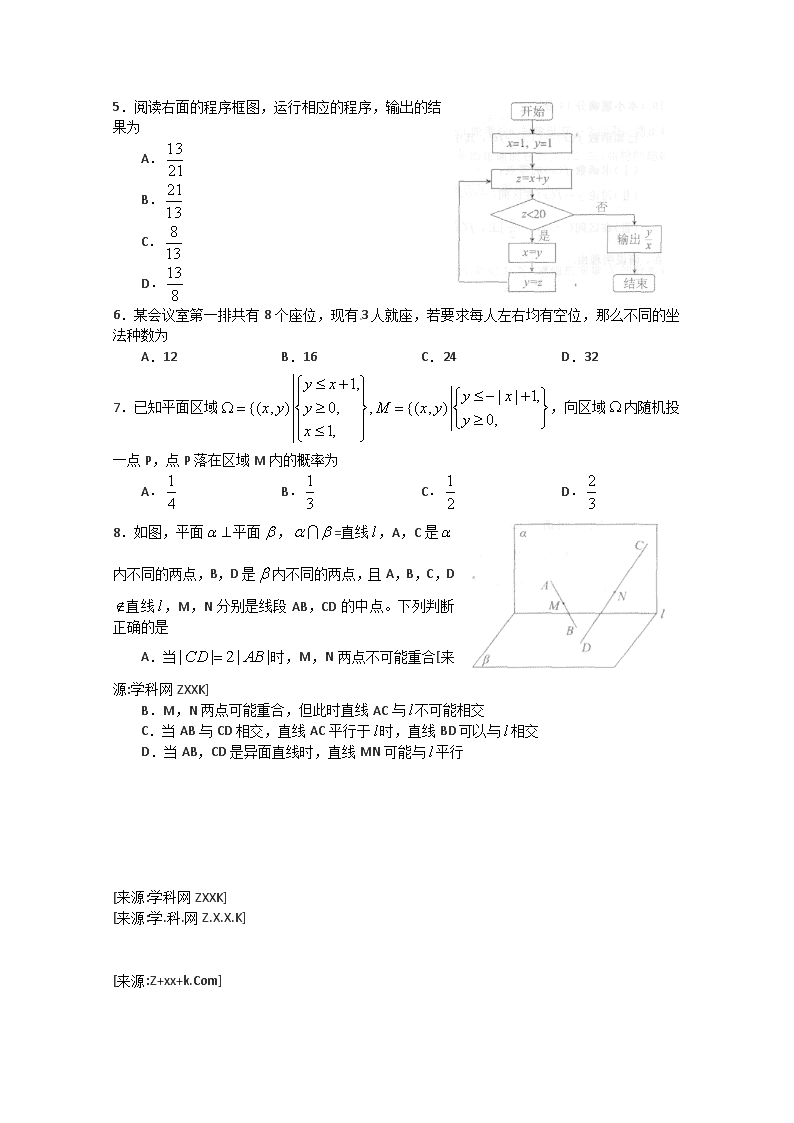
高考一模北京西城北京市西城区高三一模数学理科试题版含答案

北京市西城区2010年抽样测试 高三数学试卷（理科）‎ ‎ 本试卷分第I卷和第II卷两部分，第I卷1至2页，第II卷3至5页，共150分。考试时长120分钟。考生务必将答案答在答题纸上，在试卷上作答无效。考试结束后，将本试卷和答题纸一并交回。‎ 第I卷（选择题 共40分）‎ 一、选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，选出符合题目要求的一项。‎ ‎1．设集合，，则下列结论正确的是 ‎ A． B．‎ ‎ C． D．‎ ‎2．函数的最小值和最小正周期分别是 ‎ A． B．‎ ‎ C． D．‎ ‎3．设等差数列的前项和为，则等于 ‎ A．10 B．12‎ ‎ C．15 D．30‎ ‎4．甲乙两名运动员在某项测试中的8次成绩如茎叶图所示，，分别表示甲乙两名运动员这项测试成绩的平均数，，分别表示甲乙两名运动员这项测试成绩的标准差，则有 ‎ A．‎ ‎ B．‎ ‎ C．‎ ‎ D．[来源:学#科#网]‎ ‎[来源:学*科*网Z*X*X*K]‎ ‎5．阅读右面的程序框图，运行相应的程序，输出的结果为 ‎ A．‎ ‎ B．‎ ‎ C．‎ ‎ D．‎ ‎6．某会议室第一排共有8个座位，现有3人就座，若要求每人左右均有空位，那么不同的坐法种数为 ‎ A．12 B．‎16 ‎ C．24 D．32‎ ‎7．已知平面区域，向区域内随机投一点P，点P落在区域M内的概率为 ‎ A． B． C． D．‎ ‎8．如图，平面平面，=直线，A，C是 内不同的两点，B，D是内不同的两点，且A，B，C，D直线，M，N分别是线段AB，CD的中点。下列判断正确的是 ‎ A．当时，M，N两点不可能重合[来源:学科网ZXXK]‎ ‎ B．M，N两点可能重合，但此时直线AC与不可能相交 ‎ C．当AB与CD相交，直线AC平行于时，直线BD可以与相交 ‎ D．当AB，CD是异面直线时，直线MN可能与平行 ‎[来源:学科网ZXXK]‎ ‎[来源:学.科.网Z.X.X.K]‎ ‎[来源:Z+xx+k.Com]‎ 第II卷（非选择题 共110分）‎ 二、填空题：本大题共6小题，每小题5分，共30分。‎ ‎9．若，其中，i为虚数单位，则 。‎ ‎10．已知，，、的夹角为60°，则 。‎ ‎11．将极坐标方程化成直角坐标方程为 。‎ ‎12．如图，切于点，割线经过圆心，弦于点。已知的半径为3，，则 。 。‎ ‎13．已知双曲线的左顶点为，右焦点为 ，为双曲线右支上一点，则最小值为 。‎ ‎14．设函数的定义域为D，若存在非零实数使得对于任意，有，且，则称为M上的高调函数。‎ ‎ 如果定义域为的函数为上的高调函数，那么实数的取值范围是 。‎ ‎ 如果定义域为R的函数是奇函数，当时，，且为R上的4高调函数，那么实数的取值范围是 。‎ 三、解答题：本大题共6小题，共80分。解答应写出必要的文字说明、证明过程或演算步骤。‎ ‎15．(本小题满分12分)‎ ‎ 已知为锐角，且。‎ ‎ (I)求的值；‎ ‎ (II)求的值。‎ ‎ ‎ ‎16．（本小题满分13）‎ ‎ 在一个选拔项目中，每个选手都需要进行4轮考核，每轮设有一个问题，能正确回答者进入下一轮考核，否则被淘汰，已知某选手能正确回答第一、二、三、四轮问题的概率分别为、、、，且各轮问题能否正确回答互不影响.‎ ‎（I）求该选手进入第三轮才被淘汰的概率；‎ ‎（II）求该选手至多进入第三轮考核的概率；‎ ‎（III）该选手在选拔过程中回答过的问题的个数记为，求随机变量的分布列和期望 ‎[来源:学_科_网Z_X_X_K]‎ ‎17．（本小题满分14分）‎ ‎ 在四棱锥中，侧面底面，，为中点，底面是直角梯形，，=90°,，.‎ ‎ （I）求证：平面；‎ ‎ （II）求证：平面；‎ ‎ （III）设为侧棱上一点，，试确定的值，使得二面角为45°.‎ ‎[来源:学科网ZXXK]‎ ‎18．（本小题满分14分）‎ ‎ 椭圆：的离心率为，长轴端点与短轴端点间的距离为．‎ ‎ （I）求椭圆的方程；‎ ‎ （II）设过点的直线与椭圆交于两点，为坐标原点，若 为直角三角形，求直线的斜率．‎ ‎19．（本小题满分14分） ‎ 已知函数，其中，其中 ‎（I）求函数的零点；‎ ‎ （II）讨论在区间上的单调性；‎ ‎ （III）在区间上，是否存在最小值？若存在，求出最小值；若不存 在，请说明理由．[来源:Z,xx,k.Com]‎ ‎20．（本小题满分13分）‎ ‎ 对于各项均为整数的数列，如果(=1，2，3，…)为完全平方数，则称数 列具有“性质”．‎ ‎ 不论数列是否具有“性质”，如果存在与不是同一数列的，且同 时满足下面两个条件：①是的一个排列；②数列具有“性质”，则称数列具有“变换性质”．‎ ‎ （I）设数列的前项和，证明数列具有“性质”；‎ ‎ （II）试判断数列1，2，3，4，5和数列1，2，3，…，11是否具有“变换性质”，具有此性质的数列请写出相应的数列，不具此性质的说明理由；‎ ‎ （III）对于有限项数列：1，2，3，…，，某人已经验证当时，‎ 数列具有“变换性质”，试证明：当”时，数列也具有“变换 性质”． ‎ ‎[来源:Z|xx|k.Com]‎