广东各地高考一模练习——力学计算题

广东各地高考一模练习——力学计算题

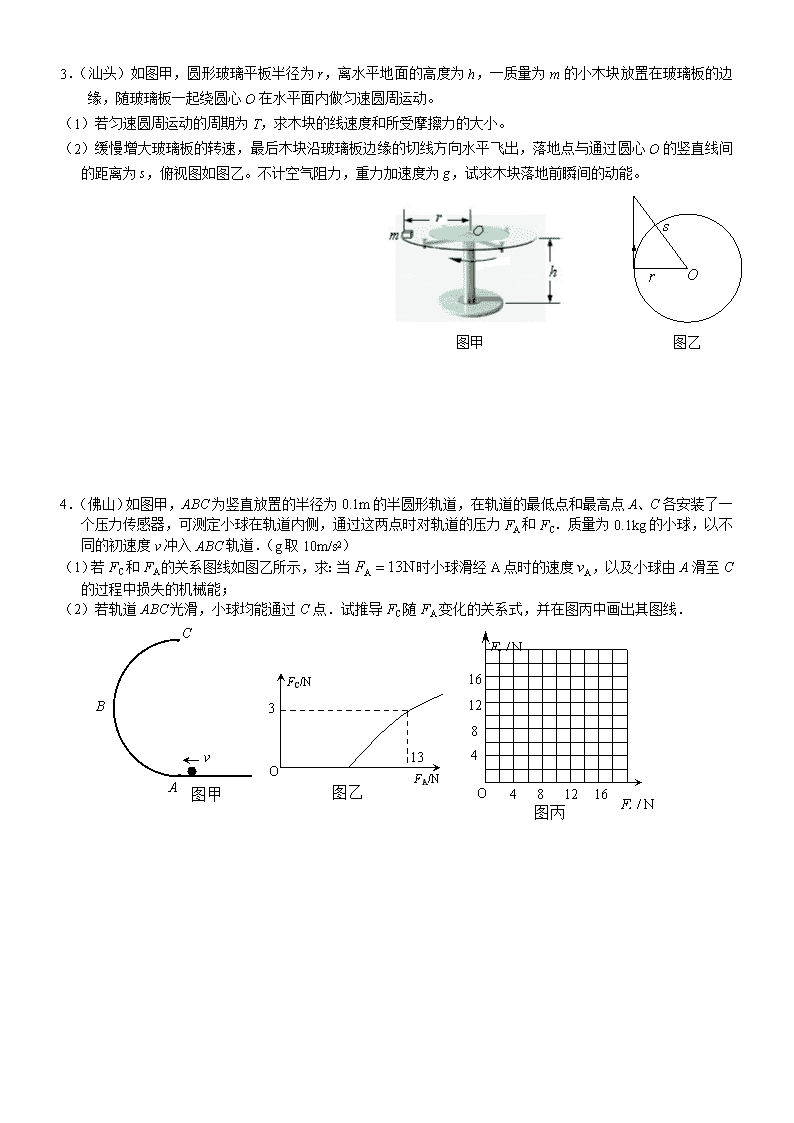
‎2012年广东各地高考一模练习——力学计算题 ‎1．（广州）如图，木板A静止在光滑水平面上，其左端与固定台阶相距x。与滑块B（可视为质点）相连的细线一端固定在O点．水平拉直细线并给B一个竖直向下的初速度，当B到达最低点时，细线恰好被拉断，B从A右端的上表面水平滑入．A与台阶碰撞无机械能损失，不计空气阻力。‎ 已知A的质量为‎2m，B的质量为m，A、B之间动摩擦因数为μ；细线长为L、能承受的最大拉力为B重力的5倍；A足够长，B不会从A表面滑出；重力加速度为g。‎ ‎（1）求B的初速度大小v0和细线被拉断瞬间B的速度大小v1；‎ ‎（2）A与台阶只发生一次碰撞，求x满足的条件；‎ 台阶 L v0‎ v1‎ A B x O B ‎（3）x在满足（2）条件下，讨论A与台阶碰撞前瞬间的速度。‎ ‎2．（18分）如图所示，质量为mA=‎2kg的木板A静止放在光滑水平面上，一质量为mB=‎1kg的小物块B从固定在地面上的光滑弧形轨道距木板A上表面某一高H处由静止开始滑下，以某一初速度v0滑上A的左端，当A向右运动的位移为L=‎0.5m时，B的速度为vB=‎4m/s，此时A的右端与固定竖直挡板相距x，已知木板A足够长（保证B始终不从A上滑出），A与挡板碰撞无机械能损失，A、B之间动摩擦因数为μ=0.2，g取‎10m/s2‎ ‎（1）求B滑上A的左端时的初速度值v0及静止滑下时距木板A上表面的高度H；‎ ‎（2）当x满足什么条件时，A与竖直挡板只能发生一次碰撞。‎ 挡板 v0‎ B A x L H ‎3．（汕头）如图甲，圆形玻璃平板半径为r，离水平地面的高度为h，一质量为m的小木块放置在玻璃板的边缘，随玻璃板一起绕圆心O在水平面内做匀速圆周运动。‎ ‎（1）若匀速圆周运动的周期为T，求木块的线速度和所受摩擦力的大小。‎ ‎（2）缓慢增大玻璃板的转速，最后木块沿玻璃板边缘的切线方向水平飞出，落地点与通过圆心O的竖直线间的距离为s，俯视图如图乙。不计空气阻力，重力加速度为g，试求木块落地前瞬间的动能。‎ 图甲 图乙 ‎4．（佛山）如图甲，ABC为竖直放置的半径为‎0.1m的半圆形轨道，在轨道的最低点和最高点A、C各安装了一个压力传感器，可测定小球在轨道内侧，通过这两点时对轨道的压力FA和FC．质量为‎0.1kg的小球，以不同的初速度v冲入ABC轨道．（g取‎10m/s2）‎ ‎（1）若FC和FA的关系图线如图乙所示，求：当时小球滑经A点时的速度，以及小球由A滑至C的过程中损失的机械能；‎ ‎（2）若轨道ABC光滑，小球均能通过C点．试推导FC随FA变化的关系式，并在图丙中画出其图线．‎ ‎16‎ FC/N FA/N O ‎13‎ ‎3‎ 图乙 O 图丙 ‎4‎ ‎8‎ ‎12‎ ‎16‎ ‎4‎ ‎8‎ ‎12‎ A B v 图甲 C ‎5．（肇庆）如下图（甲）所示，质量分别为m=‎1kg、M=‎2 kg的A、B两个小物块，用轻弹簧相连而静止在光滑水平面上，在A的左侧某处另有一质量也为m=‎1kg的小物块C，以v0=‎4m/s的速度正对A向右做匀速直线运动，一旦与A接触就将黏合在一起运动（黏合时间极短）。若在C与A接触前，瞬间使A获得一初速度vA0，并从此时刻开始计时，规定向右为正方向，A的速度随时间变化的图象如图（乙）所示（此图象仅限C与A接触前），弹簧始终未超出弹性限度，vA0 = ‎6m/s。求：‎ ‎（1）在C与A接触前，当A的速度分别为‎6m/s、‎2m/s、‎-2m/s时，求对应状态下B的速度，并据此在图（乙）中粗略画出B的速度随时间变化的图象（要求画出IT时间内）.‎ vAo A B C vo ‎（甲）‎ ‎（乙）‎ v(m·s-1)‎ t o ‎－2‎ ‎6‎ ‎4‎ T A ‎（2）当A的速度为vA时C与A接触，在接触后的运动过程中弹簧的弹性势能为Ep，当vA取何值时，Ep有最大值？试求出Ep的最大值.‎ ‎6．（深圳）如图（a）所示，“ ”型木块放在光滑水平地面上，木块水平表面AB粗糙，光滑表面BC且与水平面夹角为θ=37°。木块右侧与竖直墙壁之间连接着一个力传感器，当力传感器受压时，其示数为正值；当力传感器被拉时，其示数为负值。一个可视为质点的滑块从C点由静止开始下滑，运动过程中，传感器记录到的力和时间的关系如图（b）所示．已知sin37°=0.6，cos37°=0.8，g取‎10m/s2。求：‎ ‎0‎ F/N t/s ‎-5‎ ‎12‎ ‎1‎ ‎2‎ ‎3‎ ‎(1) 斜面BC的长度；‎ 图（a）‎ A θ B C 力传感器 ‎(2) 滑块的质量；‎ ‎(3) 运动过程中滑块克服摩擦力做的功。‎ 图（b）‎ ‎7．（惠州）单板滑雪U型池如图所示由两个完全相同的1/4圆弧滑道AB、CD和水平滑道BC构成，圆弧滑道的半径R=‎3.5m，B、C分别为圆弧滑道的最低点，B、C间的距离s=‎8.0m，假设某次比赛中运动员经过水平滑道B点时水平向右的速度v0=‎16.2m/s，运动员从B点运动到C点所用的时间t＝0.5s，从D点跃起时的速度vD=‎8.0m/s。设运动员连同滑板的质量m=‎50kg，忽略空气阻力的影响，重力加速度g取‎10m/s2。求：‎ ‎（1）运动员在B点对圆弧轨道的压力；‎ ‎（2）运动员从D点跃起后在空中完成运动的时间；‎ ‎（3）运动员从C点到D点运动的过程中需要克服摩擦阻力所做的功；‎ D C v0‎ A B R ‎8．（茂名）如图所示，地面和半圆轨道面均光滑。质量M = ‎1kg 、长L = ‎4m的小车放在地面上，其右端与墙壁的距离为S=‎3m，小车上表面与半圆轨道最低点P的切线相平。现有一质量m = ‎2kg的滑块（不计大小）以v0 = ‎6m/s的初速度滑上小车左端，带动小车向右运动。小车与墙壁碰撞时即被粘在墙壁上，已知滑块与小车表面的滑动摩擦因数μ = 0.2 ，g取‎10m/s2 。‎ ‎（1）求小车与墙壁碰撞时的速度；‎ ‎（2）要滑块能沿圆轨道运动而不脱离圆轨道，求半圆 轨道的半径R的取值。‎ ‎9．（湛江）如图所示，一辆质量为M 的小车静止在水平面上，车面上右端点有一可视为质点的滑块1，水平面上有与车右端相距为4R的固定的光滑圆弧轨道，其圆周半径为R，圆周E处的切线是竖直的，车上表面与地面平行且与圆弧轨道的末端D等高，在圆弧轨道的最低点D处，有另一个可视为质点的滑块2，两滑块质量均为m。某人由静止开始推车，当车与圆弧轨道的竖直壁CD碰撞后人即撤去推力并离开小车，车碰后靠着竖直壁静止但不粘连，滑块1和滑块2则发生碰撞，碰后两滑块牢牢粘在一起不再分离。车与地面的摩擦不计，滑块1、2与车面的摩擦系数均为，重力加速度为，滑块与车面的最大静摩擦力可认为等于滑动摩擦力。‎ O R E D A B C ‎1‎ ‎2‎ ‎（1）若人推车的力是水平方向且大小为，则在人推车的过程中，滑块1与车是否会发生相对运动？‎ ‎（2）在（1）的条件下，滑块1与滑块2碰前瞬间，滑块1的速度多大？若车面的长度为，小车质量，则的取值在什么范围内，两个滑块最终没有滑离车面？‎ ‎10．（揭阳）如图所示，质量为M的小球用长为R=‎0.45m的细绳固定于O点，从A（与O点等高）处由静止释放，与O点正下方B点处质量为的物块弹性正碰。重力加速度g=‎10m/s2‎ ‎（1）求小球碰后能上升的高度h O A B C D E F H ‎（2）已知粗糙水平地面BC及传送带的动摩擦因数均为μ=0.2，传送带长为，顺时针匀速转动，速度大小为υ=‎2m/s，DE、EF、FH的长度均为S=‎0.4m。若要保证物块碰后能落入FH间的沙坑内，求BC间的长度L 。‎ 参考答案：‎ ‎1．解析：（1）滑块B从释放到最低点，机械能守恒，有：……①‎ 在最低点，由牛顿运动定律：……②‎ 又：…③，联立①②③得：，‎ 评分说明：①②③以及两个结果正确各给1分，共5分 ‎（2）设A与台阶碰撞前瞬间，A、B的速度分别为vA和vB，由动量守恒：……④‎ 若A与台阶只碰撞一次，碰撞后必须满足…⑤，对A应用动能定理：…⑥‎ 联立④⑤⑥解得：，……⑦，即A与台阶只能碰撞一次的条件是：‎ 评分说明：④⑤⑥⑦以及结果正确各给1分，共5分 ‎（3）设x=时，A左端到台阶板前瞬间，A、B恰好达到共同速度，由动量守恒：…⑧‎ 对A应用动能定理：……⑨，联立⑧⑨得：……⑩‎ ‎ (i)当即时，AB共速后A与挡板碰撞。‎ 由⑧可得A与台阶碰撞前瞬间的速度：……⑩‎ ‎ (ii)当即时，AB共速前A就与台阶碰撞，‎ 对A应用动能定理：……，A与台阶碰撞前瞬间的速度：…… 评分说明：⑧⑨⑩各1分；（i）中的条件1分，结论1分；（ii）中条件1分，各1分。‎ ‎2．解：（1）假设B的速度从v0减为vB=‎4m/s时，A一直加速到vA，以A为研究对象，由动能定理 ‎...①（2分），代入数据解得vA=‎1m/s < vB，故假设成立（未进行此项判断扣2分）（2分） ‎ 在A向右运动位移L=‎0.5m的过程中，A、B系统动量守恒： ② （2分）‎ 联立①②解得 v0=6m/s（1分）‎ B下滑过程中机械能守恒（2分），解得 H=1.8m（1分）‎ ‎（2）设A、B与挡板碰前瞬间的速度分别为vA1、vB1，由动量守恒定律...③ （2分）‎ 以A为研究对象，由动能定理 ... ④（2分） ‎ 由于A与挡板碰撞无机械能损失，故A与挡板碰后瞬间的速度大小为，碰后系统总动量不再向右时，A与竖直挡板只能发生一次碰撞，即.... ⑤ （2分），联立③④⑤解得 x0.625m...（2分）‎ ‎3．（1）根据匀速圆周运动的规律可得木块的线速度大小 … ①（4分）‎ 木块所受摩擦力等于木块做匀速圆周运动的向心力 …②（4分）‎ ‎（2）木块脱离玻璃板后在在竖直方向上做自由落体运动，有 …③（2分）‎ 在水平方向上做匀速运动，水平位移 … ④（2分）‎ x与距离s、半径r的关系 … ⑤（2分）‎ 木块从抛出到落地前机械能守恒，得 …⑥（2分）‎ 由以上各式解得木块落地前瞬间的动能 …⑦（2分）‎ ‎4．（1）（12分）由牛顿第三定律可知，小球在A、C两点所受轨道的弹力大小，（1分）‎ 在A点由牛顿第二定律得：···①（3分），解得···②（1分）‎ 在C点由牛顿第二定律得：　····③（1分）‎ 对A至C的过程，由动能定理得：·····④（2分）‎ ‎①②③联立得···⑤（2分）‎ O ‎4‎ ‎8‎ ‎12‎ ‎16‎ ‎4‎ ‎8‎ ‎12‎ ‎16‎ 解得···⑥（2分），故损失的机械能为0.2J。‎ ‎（2）（共6分）‎ 因轨道光滑，小球由A至C的过程中机械能守恒 ‎ ‎····⑦（2分）‎ 联立①②⑥得，即···⑧（2分）‎ ‎ 图线如右图所示···⑨（2分）‎ ‎5．（18分）‎ v(m·s-1)‎ t o ‎－2‎ ‎6‎ ‎4‎ T A B 解：（1）由动量守恒定律可得：mvA0=mvA+MvB ①（2分）‎ 由①式可得： ②‎ 代入vA=‎6m/s、‎2m/s、‎-2m/s时，得到对应的VB=0、‎2m/s、‎4m/s（3分）‎ 描给的图象如答图所示。（2分，若未能画出一个周期的图象，仅根据三点描出图象且对的给1分）‎ ‎（2）无论C与A如何接触，当A、B、C具有相同的速度u时弹簧的弹性势能EP最大。‎ 由动量守恒定律可得：mv0+ mvA0=（‎2m+M）u ③（2分），由③式解得：u=2.5(m/s)‎ 设C与A碰撞前后A的瞬时速度分别为vA、v，碰撞过程中损失的机械能为ΔE，由动量守恒和能量守恒定律可得：mv0+ mvA=2mv ④（2分），⑤（2分）‎ 由④⑤式可得：⑥‎ 设弹簧的最大弹性势能为EP，由能量守恒可得 ⑦（2分）‎ 由⑦式可得：⑧（2分）‎ 由⑧式得：当vA= v0时C与A接触而黏在一起，此时不损失机械能，ΔE=0，‎ EP有最大值EPmax，将数据代入⑧式可得：EPmax=13.5(J) （1分）‎ ‎6．解：①分析滑块受力，由牛顿第二定律得：得：a1=gsinθ=‎6m/s2 ……2分 通过图像可知滑块在斜面上运动时间为：t1=1s……2分 由运动学公式得： =‎3m…2分 ②滑块对斜面的压力为：N1/=mgcosθ…2分，木板对传感器的压力为：F1=N1/sinθ…2分 A θ B C 力传感器 N1‎ N1/‎ F1‎ mg mg N2‎ f f1‎ 由图像可知：F1=12N……1分，解得：m=‎2.5Kg……1分 ‎(说明：如果从系统考虑，答案正确得满分)‎ ③滑块滑到B点的速度为：v1=a1t1=‎6m/s……1分 由图像可知：f1=5N，t2=2s……2分，=‎2m/s2…1分 ‎ ‎ =‎8m…1分，W=fs2=40J……1分 ‎7．解：（1）由N－mg= 知，N=4249.1（N）(3分），由牛三知，压力为4249.1N。(1分）‎ ‎（2）运动员从D点跃起后在空中做竖直上抛运动，设运动员上升的时间为t1，根据运动学公式vD=gt1 (3分）‎ 运动员在空中完成动作的时间：=1.6s (2分）‎ ‎（3）运动员从B点到C点，做匀变速直线运动，运动过程的平均速度 解得运动员到达C点时的速度=‎15.8m/s (3分）‎ 运动员从C点到D点的过程中,克服摩擦力和重力做功,根据动能定理 (3分)‎ 得运动员克服摩擦力做功 代入数值解得 Wf=2891J（3分）‎ ‎8．解：（1）滑块与小车的共同速度为v1 ，滑块与小车相对运动过程中动量守恒，有mv0 = (m + M)v1（2分）‎ 代入数据解得v1 = ‎4m/s（1分）‎ 设滑块与小车的相对位移为 L1 ，由系统能量守恒定律，‎ 有μmgL1 = (2分）‎ 代入数据解得L1 = ‎3m（1分）‎ 设与滑块相对静止时小车的位移为S1 ，根据动能定理，‎ 有μmgS1 =（2分）‎ 代入数据解得S1 = ‎2m（1分）‎ 因L1＜L ，S1＜S ，说明小车与墙壁碰撞前滑块与小车已具有共同速度，且共速时小车与墙壁还未发生碰撞，故小车与碰壁碰撞时的速度即v1 = ‎4m/s（1分）‎ ‎（2）滑块将在小车上继续向右做初速度为v1 = ‎4m/s，位移为L2 = L－L1 = ‎1m的匀减速运动，然后滑上圆轨道的最低点P 。‎ 若滑块恰能滑过圆的最高点，设滑至最高点的速度为v ，临界条件为mg = m（1分）‎ 根据动能定理，有－μmgL2－（2分），①②联立并代入数据解得R = ‎0.24m（1分）‎ 若滑块恰好滑至圆弧到达T点时就停止，则滑块也能沿圆轨道运动而不脱离圆轨道。‎ 根据动能定理，有－μmgL2－（2分），代入数据解得R = ‎0.6m（1分）‎ 综上所述，滑块能沿圆轨道运动而不脱离圆轨道，半圆轨道的半径必须满足R≤‎0.24m或R≥‎0.6m（1分）‎ ‎9. 解：（1）设滑块1与车不发生相对滑动，它们的加速度大小为，由牛顿第二定律有①（2分），此时滑块受到的静摩擦力大小为…②（1分），而…③‎ 由①②③解得…④（1分），又滑块1与车面的最大静摩擦力为…⑤（1分）‎ 显然，说明滑块1与车面之间没有发生相对滑动 （1分）‎ ‎（2）设滑块1与滑块2碰撞前瞬间滑块1的速度为，根据动能定理有⑥（2分）‎ 联立③⑥求得 …⑦(1分)‎ 设滑块1和2发生碰撞后的共同速度为，由动量守恒定律有： … ⑧（2分）‎ 联立⑦⑧求得 …⑨ (1分)‎ 两滑块粘合在一起后以的速度冲上光滑圆弧轨道，由于圆弧轨道的E处的切线是竖直的，则无论两滑块在圆弧轨道上运动，还是从E处竖直向上离开圆弧轨道，最后还是沿着圆弧轨道回到D处，整个过程中两滑块的机械能守恒，两滑块最终以速度冲上车面。‎ 设两滑块滑到车的左端时，若滑块刚好不滑出车面，滑块和车应有共同的速度设为，由系统的动量守恒有： …⑩ （2分）‎ 由系统的动能守恒有 ⑪（2分）‎ 联立⑨⑩⑪解得…⑫(1分)，所以当时，两个滑块最终没有滑离小车 (1分)‎ ‎10．解：（1）小球摆至B点碰前速度为υ0，由机械能守恒得：…① 1分 代入数据解得：=‎3m/s…②1分 小球与物块弹性正碰，设碰后速度分别为有υ1、υ2，有： … ③ 2分 ‎ …④ 2分，联立②③④解得：v1=‎1m/s，v2=‎4m/s（2分）‎ 小球碰后上升至高度h的过程机械能守恒，有：…⑤ (1分)‎ 代入数据解得：h=‎0.05m…⑥（1分）‎ ‎（2）设物块从D点以速度υD做平抛落入沙坑，时间为t，有：…⑦（1分），⑧（1分）‎ 由题知：，可解得：…⑨ （1分）‎ 讨论：Ⅰ）当，物块在传送带上一定做匀减速运动，此时C点速度最大为，由得： ⑩ （1分）‎ Ⅱ）当m/s

查看更多