- 2021-05-14 发布 |
- 37.5 KB |
- 75页
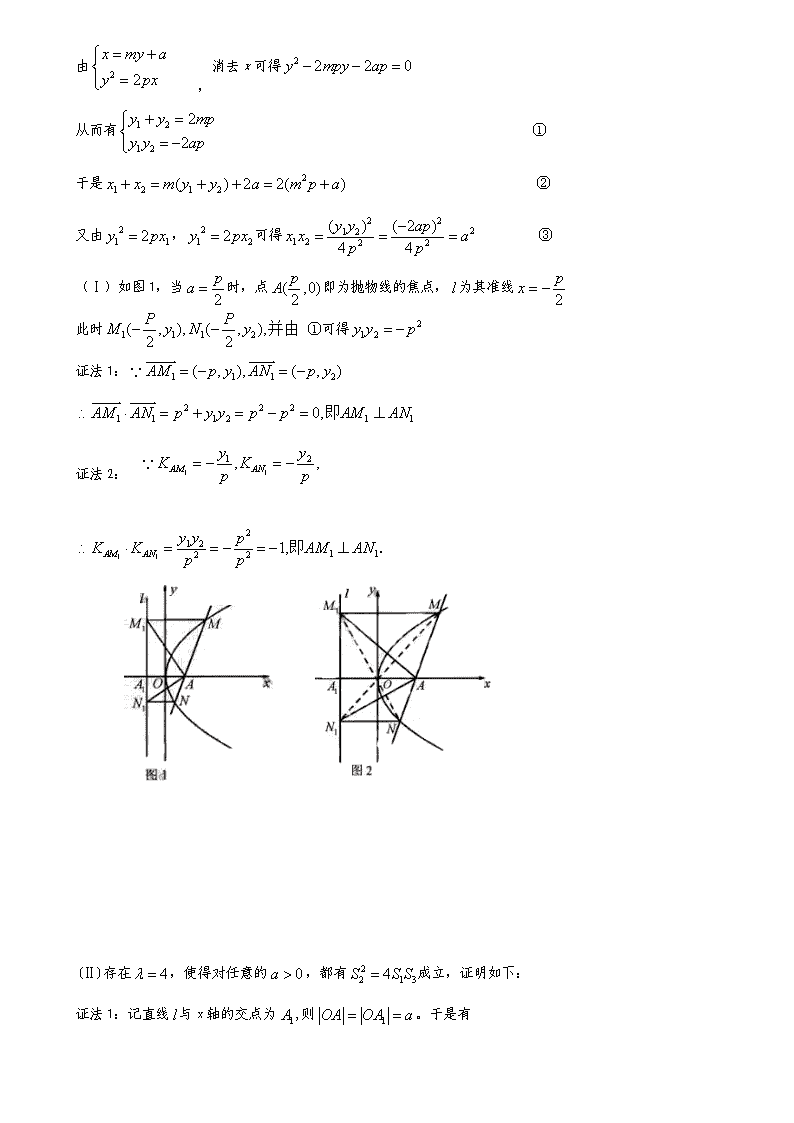


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学复习年高考年模拟汇编试题
由 ,消去x可得 从而有 ① 于是 ② 又由,可得 ③ (Ⅰ)如图1,当时,点即为抛物线的焦点,为其准线 此时 ①可得 证法1: 证法2: (Ⅱ)存在,使得对任意的,都有成立,证明如下: 证法1:记直线与x轴的交点为,则。于是有 将①、②、③代入上式化简可得 上式恒成立,即对任意成立 证法2:如图2,连接,则由可得 ,所以直线经过原点O, 同理可证直线也经过原点O 又设则 56.(2009四川卷文)(本小题满分12分) 已知椭圆的左、右焦点分别为,离心率,右准线方程为。 (I)求椭圆的标准方程; (II)过点的直线与该椭圆交于两点,且,求直线的方程。 解(I)由已知得,解得 ∴ ∴ 所求椭圆的方程为 . (II)由(I)得、 ①若直线的斜率不存在,则直线的方程为,由得 设、, ∴ ,这与已知相矛盾。 ②若直线的斜率存在,设直线直线的斜率为,则直线的方程为, 设、, 联立,消元得 ∴ , ∴ , 又∵ ∴ ∴ 化简得 解得 ∴ ∴ 所求直线的方程为 . 57.(2009全国卷Ⅱ理)(本小题满分12分) 已知椭圆的离心率为,过右焦点F的直线与相交于、两点,当的斜率为1时,坐标原点到的距离为 (I)求,的值; (II)上是否存在点P,使得当绕F转到某一位置时,有成立? 若存在,求出所有的P的坐标与的方程;若不存在,说明理由。 解 (I)设,直线,由坐标原点到的距离为 则,解得 .又. (II)由(I)知椭圆的方程为.设、 由题意知的斜率为一定不为0,故不妨设 代入椭圆的方程中整理得,显然。 由韦达定理有:........① .假设存在点P,使成立,则其充要条件为: 点,点P在椭圆上,即。 整理得。 又在椭圆上,即. 故................................② 将及①代入②解得 ,=,即. 当; 当. 58.(2009湖南卷文)(本小题满分13分) 已知椭圆C的中心在原点,焦点在轴上,以两个焦点和短轴的两个端点 为顶点的四边形是一个面积为8的正方形(记为Q). (Ⅰ)求椭圆C的方程; (Ⅱ)设点P是椭圆C的左准线与轴的交点,过点P的直线与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线的斜率的取值范围。 解 (Ⅰ)依题意,设椭圆C的方程为焦距为, 由题设条件知, 所以 故椭圆C的方程为 . (Ⅱ)椭圆C的左准线方程为所以点P的坐标, 显然直线的斜率存在,所以直线的方程为。 如图,设点M,N的坐标分别为线段MN的中点为G, 由得. ……① 由解得. ……② 因为是方程①的两根,所以,于是 =, . 因为,所以点G不可能在轴的右边, 又直线,方程分别为 所以点在正方形内(包括边界)的充要条件为 即 亦即 解得,此时②也成立. 故直线斜率的取值范围是 59.(2009福建卷理)(本小题满分13分) 已知A,B 分别为曲线C: +=1(y0,a>0)与x轴 的左、右两个交点,直线过点B,且与轴垂直,S为上 异于点B的一点,连结AS交曲线C于点T. (1)若曲线C为半圆,点T为圆弧的三等分点,试求出点S的坐标; (II)如图,点M是以SB为直径的圆与线段TB的交点,试问:是否存在,使得O,M,S三点共线?若存在,求出a的值,若不存在,请说明理由。 解 方法一 (Ⅰ)当曲线C为半圆时,如图,由点T为圆弧的三等分点得∠BOT=60°或120°. (1)当∠BOT=60°时, ∠SAE=30°. 又AB=2,故在△SAE中,有 (2)当∠BOT=120°时,同理可求得点S的坐标为,综上, (Ⅱ)假设存在,使得O,M,S三点共线. 由于点M在以SB为直线的圆上,故. 显然,直线AS的斜率k存在且k>0,可设直线AS的方程为. 由 设点 故,从而. 亦即 由得 由,可得即 经检验,当时,O,M,S三点共线. 故存在,使得O,M,S三点共线. 方法二: (Ⅰ)同方法一. (Ⅱ)假设存在a,使得O,M,S三点共线. 由于点M在以SO为直径的圆上,故. 显然,直线AS的斜率k存在且k>0,可设直线AS的方程为 由 设点,则有 故 由所直线SM的方程为 O,S,M三点共线当且仅当O在直线SM上,即. 故存在,使得O,M,S三点共线. 60.(2009辽宁卷文、理)(本小题满分12分) 已知,椭圆C以过点A(1,),两个焦点为(-1,0)(1,0)。 (1) 求椭圆C的方程; (2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。 (Ⅰ)解 由题意,c=1,可设椭圆方程为。 因为A在椭圆上,所以,解得=3,=(舍去)。 所以椭圆方程为 . (Ⅱ)证明 设直线AE方程:得,代入得 设E(,),F(,).因为点A(1,)在椭圆上, 所以, 。 又直线AF的斜率与AE的斜率互为相反数,在上式中以代,可得 , 。 所以直线EF的斜率。 即直线EF的斜率为定值,其值为。 61.(2009宁夏海南卷理)(本小题满分12分) 已知椭圆C的中心为直角坐标系xOy的原点,焦点在s轴上,它的一个顶点到两个焦点的距离分别是7和1. (Ⅰ)求椭圆C的方程; (Ⅱ)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的点,=λ,求点M的轨迹方程,并说明轨迹是什么曲线。 解 (Ⅰ)设椭圆长半轴长及半焦距分别为,由已知得 , 所以椭圆的标准方程为 (Ⅱ)设,其中。由已知及点在椭圆上可得 。 整理得,其中。 (i)时。化简得 所以点的轨迹方程为,轨迹是两条平行于轴的线段。 (ii)时,方程变形为,其中 当时,点的轨迹为中心在原点、实轴在轴上的双曲线满足的部分。 当时,点的轨迹为中心在原点、长轴在轴上的椭圆满足的部分; 当时,点的轨迹为中心在原点、长轴在轴上的椭圆; 62.(2009陕西卷文)(本小题满分12分) 已知双曲线C的方程为,离心率,顶点到渐近线的距离为。 (1)求双曲线C的方程; (2)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若,求面积的取值范围。 方法一 解(Ⅰ)由题意知,双曲线C的顶点(0,a)到渐近线, 所以所以 由 所以曲线的方程是 (Ⅱ)由(Ⅰ)知双曲线C的两条渐近线方程为 设 由 将P点的坐标代入 因为 又 所以 记 则 由 又S(1)=2, 当时,面积取到最小值,当当时,面积取到最大值 所以面积范围是 方法二(Ⅰ)由题意知,双曲线C的顶点(0,a)到渐近线, 由 所以曲线的方程是. (Ⅱ)设直线AB的方程为 由题意知 由 由 将P点的坐标代入得 设Q为直线AB与y轴的交点,则Q点的坐标为(0,m) =. 63.(2009四川卷文、理)(本小题满分12分) 已知椭圆的左、右焦点分别为,离心率,右准线方程为。 (I)求椭圆的标准方程; (II)过点的直线与该椭圆交于两点,且,求直线的方程。 解 (I)由已知得,解得 ∴ ∴ 所求椭圆的方程为 . (II)由(I)得、 ①若直线的斜率不存在,则直线的方程为,由得 设、, ∴ ,这与已知相矛盾。 ②若直线的斜率存在,设直线直线的斜率为,则直线的方程为, 设、, 联立,消元得 ∴ , ∴ , 又∵ ∴ ∴ 化简得 解得 ∴ ∴ 所求直线的方程为 64.(2009全国卷Ⅰ文)(本小题满分12分) 如图,已知抛物线与圆相交于A、B、C、D四个点。 (Ⅰ)求r的取值范围 (Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。 解:(Ⅰ)将抛物线代入圆的方程, 消去,整理得 抛物线与圆相交于、、、四个点的充要条件是:方程(1)有两个不相等的正根 ∴即。 解这个方程组得. (II)设四个交点的坐标分别为、、、。 则由(I)根据韦达定理有, 则 令,则 下面求的最大值。 方法1:由三次均值有: 当且仅当,即时取最大值。经检验此时满足题意。 方法2:设四个交点的坐标分别为、、、 则直线AC、BD的方程分别为 解得点P的坐标为。 设,由及(Ⅰ)得 由于四边形ABCD为等腰梯形,因而其面积 则将, 代入上式,并令,等 , ∴, 令得,或(舍去) 当时,;当时;当时, 故当且仅当时,有最大值,即四边形ABCD的面积最大, 故所求的点P的坐标为。 65.(2009湖北卷文)(本小题满分13分) 如图,过抛物线y2=2PX(P﹥0)的焦点F的直线与抛物线相交于M、N两点, 自M、N向准线L作垂线,垂足分别为M1、N1 (Ⅰ)求证:FM1⊥FN1: (Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为S1、、S2、,S3,试判断S22=4S1S3是否成立,并证明你的结论。 (1) 证明 方法一 由抛物线的定义得 如图,设准线l与x的交点为 而 即 故 方法二 依题意,焦点为准线l的方程为 设点M,N的坐标分别为直线MN的方程为,则有 由 得 于是,, ,故 (Ⅱ)解 成立,证明如下: 方法一 设,则由抛物线的定义得 ,于是 将与代入上式化简可得 ,此式恒成立。 故成立。 方法二 如图,设直线M的倾角为, 则由抛物线的定义得 于是 在和中,由余弦定理可得 由(I)的结论,得 即,得证。 66.(2009宁夏海南卷文)(本小题满分12分) 已知椭圆的中心为直角坐标系的原点,焦点在轴上,它的一个项点到两个 焦点的距离分别是7和1 (1)求椭圆的方程‘ (2)若为椭圆的动点,为过且垂直于轴的直线上的点,(e为椭圆C的离心率),求点的轨迹方程,并说明轨迹是什么曲线。 解(1)设椭圆长半轴长及分别为a,c,由已知得 { 解得a=4,c=3, 所以椭圆C的方程为 (Ⅱ)设M(x,y),P(x,),其中 由已知得 而,故 ① 由点P在椭圆C上得 , 代入①式并化简得 所以点M的轨迹方程为轨迹是两条平行于x轴的线段. 67.(2009湖南卷理)(本小题满分13分)在平面直角坐标系xOy中,点P到点F(3,0)的距离的4倍与它到直线x=2的距离的3倍之和记为d,当P点运动时,d恒等于 点P的横坐标与18之和 (Ⅰ)求点P的轨迹C; (Ⅱ)设过点F的直线l与轨迹C相交于M,N两点,求线段 MN长度的最大值。 解(Ⅰ)设点P的坐标为(x,y),则3︳x-2︳ 由题设 当x>2时,由①得 化简得 当时 由①得化简得 故点P的轨迹C是椭圆在直线x=2的右侧部分与 抛物线在直线x=2的左侧部分(包括它与直线x=2的交点) 所组成的曲线,参见图1 (Ⅱ)如图2所示,易知直线x=2与,的交点都是 A(2,),B(2,), 直线AF,BF的斜率分别为=,=. 当点P在上时,由②知 . ④ 当点P在上时,由③知 ⑤ 若直线l的斜率k存在,则直线l的方程为 (i)当k≤,或k≥,即k≤-2 时,直线I与轨迹C的两个交点M(,),N(,)都在C 上,此时由④知 ∣MF∣= 6 - ∣NF∣= 6 - 从而∣MN∣= ∣MF∣+ ∣NF∣= (6 - )+ (6 - )=12 - ( +) 由 得 则,是这个方程的两根,所以+=*∣MN∣=12 - (+)=12 - 因为当 当且仅当时,等号成立。 (2)当时,直线L与轨迹C的两个交点 分别在上,不妨设点在上,点上,则④⑤知, 设直线AF与椭圆的另一交点为E 所以。而点A,E都在上,且 有(1)知 若直线的斜率不存在,则==3,此时 综上所述,线段MN长度的最大值为. 68.(2009福建卷文)(本小题满分14分) 已知直线经过椭圆 的左顶点A和上顶点D,椭圆的右顶点为,点和椭圆上位于轴上方的动点,直线,与直线 分别交于两点。 (I)求椭圆的方程; (Ⅱ)求线段MN的长度的最小值; (Ⅲ)当线段MN的长度最小时,在椭圆上是否存在这样的点,使得的面积为?若存在,确定点的个数,若不存在,说明理由 解 方法一(I)由已知得,椭圆的左顶点为上顶点为 故椭圆的方程为 (Ⅱ)直线AS的斜率显然存在,且,故可设直线的方程为, 从而 由得0 设则得,从而 即又 由得 故 又 当且仅当,即时等号成立 时,线段的长度取最小值 (Ⅲ)由(Ⅱ)可知,当取最小值时, 此时的方程为 要使椭圆上存在点,使得的面积等于,只须到直线的距离等于,所以在平行于且与距离等于的直线上。 设直线 则由解得或 69.(2009年上海卷理)(本题满分16分) 已知双曲线设过点的直线l的方向向量 (1) 当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离; (2) 证明:当>时,在双曲线C的右支上不存在点Q,使之到直线l的距离为。 (1)解 双曲线C的渐近线 · 直线l的方程 · 直线l与m的距离 (2)证明 方法一设过原点且平行与l的直线 则直线l与b的距离 当 又双曲线C的渐近线为 双曲线C的右支在直线b的右下方, 双曲线右支上的任意点到直线的距离为。 故在双曲线的右支上不存在点,使之到直线的距离为。 (2)方法二 双曲线的右支上存在点到直线的距离为, 则 由(1)得, 设 当,0 将 代入(2)得 (*) 方程(*)不存在正根,即假设不成立 故在双曲线C的右支上不存在Q,使之到直线l 的距离为 70.(2009上海卷文)(本题满分16分) 已知双曲线C的中心是原点,右焦点为F,一条渐近线m:,设过点A的直线l的方向向量。 (1) 求双曲线C的方程; (1) 若过原点的直线,且a与l的距离为,求K的值; (2) 证明:当时,在双曲线C的右支上不存在点Q,使之到直线l的距离为. (1)解 设双曲线的方程为 ,解得,双曲线的方程为 (2)解 直线,直线 由题意,得,解得 (3)证明 方法一 设过原点且平行于的直线 则直线与的距离当时, 又双曲线的渐近线为 双曲线的右支在直线的右下方, 双曲线右支上的任意点到直线的距离大于。 故在双曲线的右支上不存在点,使之到直线的距离为 (3)方法二 假设双曲线右支上存在点到直线的距离为, 则 由(1)得 设, 当时,; 将代入(2)得 , 方程不存在正根,即假设不成立, 故在双曲线的右支上不存在点,使之到直线的距离为 71.(2009重庆卷理)(本小题满分12分) 已知以原点为中心的椭圆的一条准线方程为,离心率,是椭圆上的动点. (Ⅰ)若的坐标分别是,求的最大值; (Ⅱ)如题图,点的坐标为,是圆上的点,是点在轴上的射影,点满足条件:,.求线段的中点的轨迹方程; 解 (Ⅰ)由题设条件知焦点在y轴上,故设椭圆方程为(a >b> 0 ). 设,由准线方程得.由得,解得 a = 2 ,c = ,从而 b = 1,椭圆方程为 . 又易知C,D两点是椭圆的焦点,所以, 从而,当且仅当, 即点M的坐标为时上式取等号,的最大值为4 . (II)如图(20)图,设 .因为,故 ① 因为 所以 . ② 记P点的坐标为,因为P是BQ的中点 所以 由因为 ,结合①,②得 故动点P的估计方程为 72.(2009重庆卷文)(本小题满分12分) 已知以原点为中心的双曲线的一条准线方程为,离心率. (Ⅰ)求该双曲线的方程; (Ⅱ)如题(20)图,点的坐标为,是圆上的点,点在双曲线右支上,求的最小值,并求此时点的坐标; 解 (Ⅰ)由题意可知,双曲线的焦点在轴上,故可设双曲线的方程为,设,由准线方程为得,由得 解得 从而,该双曲线的方程为. (Ⅱ)设点D的坐标为,则点A、D为双曲线的焦点, 所以 ,是圆上的点,其圆心为,半径为1,故 从而 当在线段CD上时取等号,此时的最小值为 直线CD的方程为,因点M在双曲线右支上,故 由方程组 解得 所以点的坐标为. 2005—2008年高考题 一、选择题 1.(2008湖北卷10)如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞 向月球,在月球附近一点轨进入以月球球心为一个焦点的椭圆 轨道Ⅰ绕月飞行,之后卫星在变点第二次变轨进入仍以月球球心为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在点第三次变轨进入以为圆心的圆形轨道Ⅲ绕月飞行,若用和分别表示椭轨道Ⅰ和Ⅱ的焦距,用和分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子: ①; ②; ③; ④<. 其中正确式子的序号是 ( ) A. ①③ B. ②③ C. ①④ D. ②④ 答案 B 2.(2008江西理7)已知、是椭圆的两个焦点,满足的点总在椭圆内部,则椭圆离心率的取值范围是 ( ) A. B. C. D. 答案 C 3.(2008全国Ⅱ理9)设,则双曲线的离心率的取值范围是 ( ) A. B. C. D. 答案 B 4.(2008海南理11)已知点P在抛物线y2 = 4x上,那么点P到点Q(2,-1)的距离与 点P 到抛物线焦点距离之和取得最小值时,点P的坐标为 ( ) A.(,-1) B.(,1) C.(1,2) D.(1,-2) 答案 A 5.(2008辽宁理10)已知点P是抛物线上的一个动点,则点P到点(0,2)的距 离与P到该抛物线准线的距离之和的最小值为 ( ) A. B. C. D. 答案 A 6.(2008天津文7)设椭圆(,)的右焦点与抛物线的焦 点相同,离心率为,则此椭圆的方程为 ( ) A. B. C. D. 答案 B 7.(2007重庆文)已知以F1(2,0),F2(2,0)为焦点的椭圆与直线有且仅有一个交点,则椭圆的长轴长为 ( ) A. B. C. D. 答案 C 8.(2007浙江文)已知双曲线 的左、右焦点分别为F1、F2,P 是准线上一点,且PF1⊥PF2,|PF1||PF2 |=4ab,则双曲线的离心率是 ( ) A. B. C.2 D.3 答案 B 9.(2007天津文)设双曲线的离心率为,且它的一条准线与 抛物线的准线重合,则此双曲线的方程为 ( ) A. B. C. D. 答案 D 10. (2006上海春季15) 若,则“”是“方程表示双曲线” 的 ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 答案 A 11.(2005年上海理15) 过抛物线的焦点作一条直线与抛物线相交于A、B两点, 它们的横坐标之和等于5,则这样的直线 ( ) A.有且仅有一条 B.有且仅有两条 C.有无穷多条 D.不存在 答案 B 解析 的焦点是(1,0),设直线方程为 (1),将(1)代入抛物线方程可得,x显然有两个实根,且都大于0,它们的横坐标之和是,选B. 二、填空题 12.(2008湖南理12)已知椭圆(a>b>0)的右焦点为F,右准线为,离心率 e=过顶点A(0,b)作AM,垂足为M,则直线FM的斜率等于 . 答案 13.(2008江苏12)在平面直角坐标系中,椭圆1( 0)的焦距为2,以O 为圆心,为半径的圆,过点作圆的两切线互相垂直,则离心率= . 答案 14.(2008全国Ⅰ理15)在中,,.若以为焦点的 椭圆经过点C,则该椭圆的离心率 . 答案 15.(2008浙江理12)已知为椭圆的两个焦点,过的直线交椭圆于 A、B两点.若,则=______________. 答案 8 16.(2008上海春季7) 已知是双曲线右支上的一点,双曲线的一条渐近线方 程为. 设分别为双曲线的左、右焦点. 若,则 . 答案 5 17.(2007山东理)设O是坐标原点,F是抛物线的焦点,A是抛物线上 的一点,与轴正向的夹角为,则为 . 答案 18.(2007上海春季6) 在平面直角坐标系中,若抛物线上的点到该抛物线的 焦点的距离为6,则点P的横坐标 . 答案 5 19.(2006上海理7) 已知椭圆中心在原点,一个焦点为F(-2,0),且长轴长是短轴长 的2倍,则该椭圆的标准方程是 . 答案 20.(2005江西理)以下四个关于圆锥曲线的命题中: ①设A、B为两个定点,k为非零常数,,则动点P的轨迹为双曲线; ②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若则动点 P的轨迹为椭圆; ③方程的两根可分别作为椭圆和双曲线的离心率; ④双曲线有相同的焦点. 其中真命题的序号为 (写出所有真命题的序号) 答案 ③④ 三、解答题 21.(2008全国Ⅰ理21)双曲线的中心为原点,焦点在轴上,两条渐近线分别为l1,l2, 经过右焦点垂直于l1的直线分别交l1、l2于两点.已知成等差数 列,且与同向. (Ⅰ)求双曲线的离心率; (Ⅱ)设被双曲线所截得的线段的长为4,求双曲线的方程. 解:(Ⅰ)设,, 由勾股定理可得: 得:,, 由倍角公式,解得,则离心率. (Ⅱ)过直线方程为,与双曲线方程联立 将,代入,化简有 将数值代入,有,解得 故所求的双曲线方程为。 第二部分 四年联考汇编 2010年联考题 题组二(5月份更新) 1.(马鞍山学业水平测试)双曲线的渐近线方程是 A. B. C. D. 答案 A 2. (昆明一中二次月考理)已知是以为焦点的椭圆上的一点,若,,则此椭圆的的离心率为( ) A. B. C. D. 答案:D 3.(师大附中理)如图2,设在椭圆中,和是短轴端点,是椭圆上 不同于的任一点,直线分别交轴于,,则 A.4 B.4.5 C.5 D.5.5 答案:C 4. (马鞍山学业水平测试)椭圆的焦点坐标为 A. B. C. D. 答案 C 5.(马鞍山学业水平测试)过抛物线的焦点的直线交抛物线于、两点,如果,则 A.9 B.8 C.7 D.6 答案 B 6. (马鞍山学业水平测试)已知动点P(x,y)满足,则动点P的轨迹是 A.双曲线 B.双曲线左支 C. 双曲线右支 D. 一条射线 答案 C 7.(昆明一中三次月考理)若抛物线的焦点与椭圆的左焦点重合,则p的值为 A.-2 B.2 C.-4 D.4 答案:C 8.(昆明一中三次月考理)设双曲线的半焦距为c,直线l过A(a,0),B(0,b)两点,若原点O到l的距离为,则双曲线的离心率为 A. B.2 C. D. 答案:A 9.(马鞍山学业水平测试)方程表示的曲线为 A. 抛物线 B. 椭圆 C. 双曲线 D.圆 答案 A 10. (安徽六校联考)简化北京奥动会主体育场“鸟巢”的钢结构俯视图 如图所示,内外两圈的钢骨架是离心率相同的椭圆,外层椭圆顶点向内 层椭圆引切线、.设内层椭圆方程为,则外层椭 圆方程可设为.若与的斜率之积为,则椭圆的离心率为( ) A. B. C. D. 答案A 11. (玉溪一中期中) 从双曲线的左焦点F引圆的切线l,切点为T,且l交双曲线的右支于点P. 若点M是线段FP的中点,O为坐标原点,则|OM|-|TM|=( ) A. B. C. D. 答案:B 12.(池州市七校元旦调研)过双曲线的右顶点作斜率为的直线,该直线与双曲线的两条渐近线的交点分别为.若,则双曲线的离心率是 ( ) A B. C. D. 答案 C 【解析】对于,则直线方程为,直线与两渐近线的交点为B,C,,则有 ,因. 13.(岳野两校联考)双曲线的一条准线被它的两条渐近线所截得线段长度恰好为它的一个焦点到一条渐近线的距离,则该双曲线的离心率是( ) A.3 B.2 C. D. 答案 B 14.(岳野两校联考)如图,F为抛物线的焦点,A、B、C在抛物线上,若,则( ) A. 6 B. 4 C. 3 D.2 答案 A 15.(三明市三校联考)设椭圆(,)的右焦点与抛物线的焦点相同,离心率为,则此椭圆的方程为 ( ) A. B. C. D. 答案B 16.(祥云一中月考理)如果双曲线的离心率为,则该双曲线的渐近线方程为( ) A. B. C. D. 答案:C 17.(三明市三校联考)已知椭圆的左焦点分别为,过作倾斜角为的直线与椭圆的一个交点P,且轴,则此椭圆的离心率为 ( ) A. B. C. D. 答案A 18.(昆明一中四次月考理)已知、分别是双曲线的左、右焦点,P为双曲线左支上任意一点,若 的最小值为8,则双曲线的离心率的取值范围为( ) (A) (B) (C) (D) 答案:A 二、填空题 1.(马鞍山学业水平测试)设抛物线型拱桥的顶点距水面2米,测量水面宽度为8米.当水面上升1米后,水面宽度 为 米. 答案 2.(昆明一中一次月考理)设F为抛物线的焦点,与抛物线相切于点的直线l与x轴的交点为Q,__. 答案:90° 3.(玉溪一中期中)点P(3,1)在椭圆的右准线上,过P点且方向向量为的光线经直线y=-2反射后通过椭圆的右焦点,则这个椭圆的离心率为 . 答案: 4. 与双曲线有共同的渐近线,且过点的双曲线的方程为 . 答案 5.(昆明一中四次月考理)抛物线上的点M到焦点F的距离为4,则点M的横坐标是 . 答案:3 6.(昆明一中四次月考理)若球的表面积为,边长为2的正三角形的三个顶点在球的表面上,则球心到平面的距离为 . 答案: 7.(安庆市四校元旦联考)若椭圆的左、右焦点分别为,线 段被抛物线的焦点分成5 :3的两段,则此椭圆的离心率为 答案 8.(玉溪一中期中文)双曲线的右支上存在一点,它到右焦点及 左准线的距离相等,则双曲线离心率的取值范围是 。 答案: 9.(祥云一中月考理)两个正数、的等差中项是,一个等比中项是,且则 双曲线的离心率为 。 答案: 三、解答题 1. (马鞍山学业水平测试)(本小题满分8分) 设椭圆的中心在原点,焦点在轴上,离心率,且过点,求这个椭圆的方程. 解:∵椭圆的中心在原点,焦点在轴上且过点 ∴………………………………………………………………………………3分 又,∴,∴……………………………6分 故这个椭圆方程是…………………………………………………8分 20090423 2.(池州市七校元旦调研)已知,椭圆C过点A,两个焦点为(-1,0),(1,0)。 (1)求椭圆C的方程; (2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数, 证明直线EF的斜率为定值,并求出这个定值。 解: (Ⅰ)由题意,c=1,可设椭圆方程为,解得,(舍去) 所以椭圆方程为。 ……………4分 (Ⅱ)设直线AE方程为:,代入得 设,,因为点在椭圆上,所以 ; 又直线AF的斜率与AE的斜率互为相反数,在上式中以—K代K,可得 ; 所以直线EF的斜率. 3.(肥城市第二次联考)(本小题满分12分) 如图,在直角坐标系中,已知椭圆的离 心率e=,左右两个焦分别为.过右焦点且与轴垂直的 直线与椭圆相交M、N两点,且|MN|=1. (Ⅰ) 求椭圆的方程; (Ⅱ) 设椭圆的左顶点为A,下顶点为B,动点P满足,()试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆上. 解:(Ⅰ)∵轴,∴,由椭圆的定义得:,------1分 ∵, ∴,-----------------------------------3分 又得 ∴ ∴,-------------------------------4分 ∴所求椭圆C的方程为.-----------------------------------5分 (Ⅱ)由(Ⅰ)知点A(-2,0),点B为(0,-1),设点P的坐标为 则,, 由-4得-, ∴点P的轨迹方程为------------------------------------7分 设点B关于P的轨迹的对称点为,则由轴对称的性质可得:, 解得:,------------------------------9分 ∵点在椭圆上,∴ ,整理得解得或 ∴点P的轨迹方程为或,-------------------------------------------11分 经检验和都符合题设, ∴满足条件的点P的轨迹方程为或.----------------12分 4. (马鞍山学业水平测试)(本小题满分10分) 已知椭圆C:的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,且向量与共线. (Ⅰ)求椭圆的离心率e; (Ⅱ)若是椭圆C的一条准线,求椭圆C的方程. 解:(Ⅰ)∵,∴.……………………………2分 ∵是共线向量,∴,∴b=c,故.……………4分 (Ⅱ) 由, 又,…………………………8分 所以椭圆C的方程为…………………………………………………………10分 5. (哈师大附中、东北师大附中、辽宁省实验中学)如图,设抛物线的准线与轴交于,焦点为;以为焦点,离心率的椭圆与抛物线在轴上方的交点为,延长交抛物线于点,是抛物线上一动点,且M在与之间运动. (1)当时,求椭圆的方程; (2)当的边长恰好是三个连续的自然数时,求面积的最大值. 解:(1)当时, ,则 设椭圆方程为,则又,所以 所以椭圆C2方程为 ………… (2)因为,,则,,设椭圆方程为 由,得 ………… 即,得代入抛物线方程得,即 ,, 因为的边长恰好是三个连续的自然数,所以 ………… 此时抛物线方程为,,直线方程为:. 联立,得,即, 所以,代入抛物线方程得,即 ∴. 设到直线PQ的距离为 , 则 ………… 当时,, 即面积的最大值为. ………… 6. (玉溪一中期中)(本小题12分)已知A,B,C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆的中心O,且,, (Ⅰ)求椭圆的方程; (Ⅱ)如果椭圆上的两点P,Q使的平分线垂直于OA,是否总存在实数,使得?请说明理由; . 解: (1)以O为原点,OA所在直线为x轴建立 平面直角坐标系,则, 设椭圆方程为,不妨设C在x轴上方, 由椭圆的对称性,, 又,即为等腰直角三角形, 由得:,代入椭圆方程得:, 即,椭圆方程为; (2)假设总存在实数,使得,即, 由得,则, 若设CP:,则CQ:, 由, 由得是方程的一个根, 由韦达定理得:,以代k得, 故,故, 即总存在实数,使得. 题组一(1月份更新) 一、选择题 1、(2009东莞一模)设是椭圆上的点.若是椭圆的两个焦点,则等于( ) A.4 B5 C.8 D.10 答案 D 2、(2009滨州一模)已知点,,,动圆与直线切于点,过、与圆相切的两直线相交于点,则点的轨迹方程为 . . . . 答案 A 3、(2009茂名一模)已知是椭圆的两个焦点,过且与椭圆长轴垂直的直线交椭圆于A、B两点,若是等腰直角三角形,则这个椭圆的离心率是( ) A、 B、 C、 D、 答案 C 4、(2009临沂一模)已知双曲线的两个焦点F1(,0),F2(,0),M是此双曲线上的一点,且则该双曲线的方程是 A、 B、 C、 D、 答案 A 5、(2009汕头一模)中心在原点,焦点在x轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为,则双曲线方程为( ) A、x2-y2=2 B、x2-y2= C、x2-y2=1 D、x2-y2= 答案 A 6、(2009泰安一模)已知曲线C:y=2x,点 A(0,-2)及点B(3,a),从点A观察点B,要使实现不被曲线C挡住,则实数a的取值范围是 A.(4,+) B.(,4) C.(10,) D. 答案 D 7、(2009韶关一模)圆上的动点到直线的最小距离为 A.1 B. C. D. 答案 B 8、(2009潍坊一模)抛物线的准线与双曲线等的两条渐近线所围成的三角形面积等于 (A) (B) (C)2 (D) 答案 A 9、(2009深圳一模)设平面区域是由双曲线的两条渐近线和椭圆的右准线所围成的三角形(含边界与内部).若点,则目标函数的最大值为 A. B. C. D. 答案 C 10、(2009湛江一模)过点A (3 , 0 ) 的直线l与曲线 有公共点,则直线l斜率的取值范围为 A.(, ) B.[, ] C.(, ) D.[, ] 答案 D 二、填空题 1、(2009临沂一模)已知A、B是抛物线上的两点,线段AB的中点为M(2,2),则|AB|等于 答案 2、(2009上海十四校联考)以原点为顶点,x轴为对称轴且焦点在上的抛物线方程是 答案 。 3、(2009日照一模)抛物线的焦点坐标是_______________。 答案 4、(2009冠龙高级中学3月月考)以椭圆中心为顶点,右顶点为焦点的抛物线的标准方程为_____________。 答案 5、(2009上海普陀区)设联结双曲线与(,)的个顶点的四边形面积为,联结其个焦点的四边形面积为,则的最大值为 . 答案 6、(2009泰安一模)P为双曲线右支上一点,M、N分别是圆 上的点,则|PM|-|PN|的最大值为 答案 5 7、(2009闵行三中模拟)已知为双曲线的右顶点,F是双曲线的右焦点,则|AF|=_______。 答案 1 8、(2009枣庄一模)设椭圆的右焦点与抛物线的 焦点相同,离心率为,则此椭圆的标准方程为 。 答案 9、(2009上海青浦区)已知是椭圆上的一个动点,则 的最大值是 答案 5 三、解答题 1、(2009滨州一模)已知方向向量为的直线过点和椭圆的右焦点,且椭圆的离心率为. (I)求椭圆的方程; (II)若已知点,点是椭圆上不重合的两点,且,求实数的取值范围. (1)∵直线的方向向量为 ∴直线的斜率为,又∵直线过点 ∴直线的方程为 ∵,∴椭圆的焦点为直线与轴的交点 ∴椭圆的焦点为 ∴,又∵ ∴ ,∴ ∴椭圆方程为 (2)设直线MN的方程为 由,得 设坐标分别为 则 (1) (2) >0∴, ∵,显然,且 ∴∴ 代入(1) (2),得 ∵,得,即 解得且. 2、(2009广州一模)已知动圆C过点A(-2,0),且与圆M:(x-2)2+x2=64相内切 (1)求动圆C的圆心的轨迹方程; (2)设直线l: y=kx+m(其中k,m∈Z)与(1)所求轨迹交于不同两点B,D,与双曲线交于不同两点E,F,问是否存在直线l,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由. (本题主要考查圆、椭圆、直线等基础知识和数学探究,考查数形结合、类与整的数学思想方法,以及推理论证能力、运算求解能力和创新意识) 解:(1)圆M:(x-2)2+x2=64,圆心M的坐标为(2,0),半径R=8. ∵|AM|=4查看更多