安徽省芜湖市第一中学高考物理一轮复习 第三章 第11讲 连接体问题1、加速度相等型教案（通用）

安徽省芜湖市第一中学高考物理一轮复习 第三章 第11讲 连接体问题1、加速度相等型教案（通用）

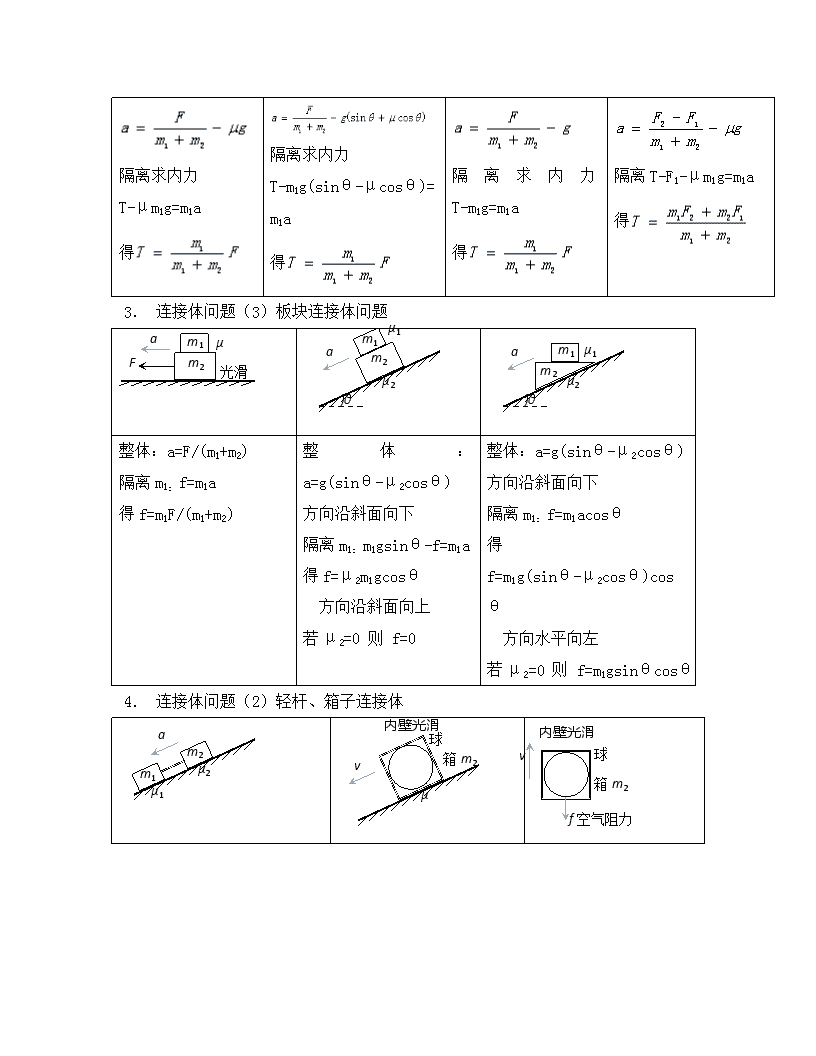
连接体问题1、加速度相等型 ‎ 班级__________ 座号_____ 姓名__________ 分数__________‎ 一、知识清单 ‎1． 应用整体法与隔离法处理连接体问题 ‎(1)连接体问题的类型 物物连接体、轻杆连接体、弹簧连接体、轻绳连接体．‎ ‎(2)整体法的选取原则 若连接体内各物体具有相同的加速度，且不需要求物体之间的作用力，可以把它们看成一个整体，分析整体受到的合外力，应用牛顿第二定律求出加速度(或其他未知量)．‎ ‎(3)隔离法的选取原则 若连接体内各物体的加速度不相同，或者要求出系统内 各物体之间的作用力时，就需要把物体从系统中隔离出来，应用牛顿第二定律列方程求解．‎ ‎(4)整体法、隔离法的交替运用 若连接体内各物体具有相同的加速度，且要求出物体之间的作用力时，一般采用“先整体求加速度，后隔离求内力”．‎ ‎2． 连接体问题（1）轻绳相连加速度相同的连接体 m1‎ m2‎ F μ μ a m1‎ m2‎ F μ μ a m1‎ m2‎ F μ μ a m1‎ m2‎ F a m1‎ m2‎ F μ μ a m3‎ μ 求m2、m3间作用力,将m1和m2看作整体 整体求加速度 整体求加速度 整体求加速度 m1‎ m2‎ F2‎ μ μ a F1‎ 隔离求内力 T-μm‎1g=m‎1a 得 隔离求内力 T-m‎1g(sinθ-μcosθ)=m‎1a 得 隔离求内力T-m‎1g=m‎1a 得 隔离T-F1-μm‎1g=m‎1a 得 ‎3． 连接体问题（3）板块连接体问题 m1‎ m2‎ μ 光滑 a F m1‎ m2‎ μ1‎ μ2‎ a ‎)θ m1‎ μ1‎ μ2‎ a ‎)θ m2‎ 整体：a=F/(m1+m2)‎ 隔离m1：f=m‎1a 得f=m‎1F/(m1+m2)‎ 整体：a=g(sinθ-μ2cosθ)‎ 方向沿斜面向下 隔离m1：m1gsinθ-f=m‎1a 得f=μ‎2m1gcosθ 方向沿斜面向上 若μ2=0 则 f=0‎ 整体：a=g(sinθ-μ2cosθ)‎ 方向沿斜面向下 隔离m1：f=m1acosθ 得f=m‎1g(sinθ-μ2cosθ)cosθ 方向水平向左 若μ2=0 则 f=m1gsinθcosθ ‎4． 连接体问题（2）轻杆、箱子连接体 m1‎ m2‎ μ1‎ μ2‎ a 球m1‎ m2‎ μ v 内壁光滑 箱m2‎ 球m1‎ v 内壁光滑 箱m2‎ f空气阻力 隔离m1：m‎1g(sinθ-μ1cosθ)-T=m‎1a 隔离m2：m‎2g(sinθ-μ2cosθ)+T=m‎2a 得 ‎（1）若μ1=μ2 T=0，即杆无弹力 ‎（2）若μ1<μ2 T>0，即杆为拉力 ‎（3）若μ1>μ2 T<0，即杆为压力 ‎①下滑 整体：a=g(sinθ-μcosθ)‎ 隔离m1：m1gsinθ-FN=m‎1a 得：FN=μm1gcosθ 方向向上，即左侧壁有弹力 若μ=0 FN=0，即球无弹力 ‎②上冲 方向向下，即右侧壁有弹力 ‎①上抛 整体：a=g+f/(m1+m2)‎ 隔离m1：m‎1g+FN=m‎1a 得：FN=m‎1f/(m1+m2)‎ 方向向下，即上侧壁有弹力 若f=0则FN=0，即球无弹力 ‎②下落 方向向上，即下侧壁有弹力 ‎5． 连接体问题（4）轻绳绕滑轮加速度问题 m1‎ m2‎ a a μ m1‎ m2‎ a a 隔离m1：T-μm‎1g=m‎1a 隔离m2：m‎2g-T=m‎2a 得，‎ 隔离m1：m‎1g-T=m‎1a 隔离m2：T-m‎2g=m‎2a 得，‎ 若μ=0， 且m2<a2‎ C．a1μ2‎ ‎.在此过程中，滑块B对A的压力为（ ）‎ A. B．(μ1－μ2)mgcosθ C．mgsinθ－μ1mgcosθ D．0‎ ‎20．如图所示，倾角为α的斜面是光滑的，斜面上有一滑块A，A的水平上表面站有质量为m的人，则当A从斜面上自由滑下时，要使人相对滑块A静止，则人与滑块间的摩擦力大小为（ ）‎ A．mgsinα B．mgcosα C．0 D．mgsinα•cosα ‎21．（多选）如图10所示，位于光滑水平桌面上的物块P用跨过定滑轮的轻绳与小托盘相连，托盘内有砝码。托盘与砝码的总质量为m，P的质量为‎2m，重力加速度为g。释放后，P从静止开始沿桌面运动的过程中，下列说法正确的是(　　)‎ A．托盘运动的加速度大小为g B．P运动的加速度大小为 C．托盘对轻绳的拉力大小为mg D．砝码处于超重状态 ‎22．(多选)一足够长的倾角为θ的斜面固定在水平面上，在斜面顶端放置一长木板，木板与斜面之间的动摩擦因数为μ，木板上固定一力传感器，连接传感器和光滑小球间是一平行于斜面的轻杆，如图所示，当木板固定时，传感器的示数为F1.现由静止释放木板，木板沿斜面下滑，稳定时传感器的示数为F2.则下列说法正确的是（ ）‎ A．稳定后传感器的示数一定不为零 B．tanθ＝ C．tanθ＝ D．tanθ＝ ‎23．（多选）如图9所示，A、B、C三球的质量均为m，轻质弹簧一端固定在斜面顶端、另一端与A球相连，A、B间由一轻质细线连接，B、C间由一轻杆相连。倾角为θ的光滑斜面固定在地面上，弹簧、细线与轻杆均平行于斜面，初始系统处于静止状态，细线被烧断的瞬间，下列说法正确的是(　　)‎ A．A球的加速度沿斜面向上，大小为gsin θ B．C球的受力情况未变，加速度为0‎ C．B、C两球的加速度均沿斜面向下，大小均为gsin θ D．B、C之间杆的弹力大小为0‎ ‎24．如图2所示，质量为‎4 kg的物体A静止在竖直的轻弹簧上面。质量为‎1 kg的物体B用细线悬挂起来，A、B紧挨在一起但A、B之间无压力。某时刻将细线剪断，则细线剪断瞬间，B对A的压力大小为(取g＝‎10 m/s2)（ ）‎ 图2‎ A．0 N B．8 N C．10 N D．50 N