高考数学理二轮复习几何体与球切接的问题

高考数学理二轮复习几何体与球切接的问题

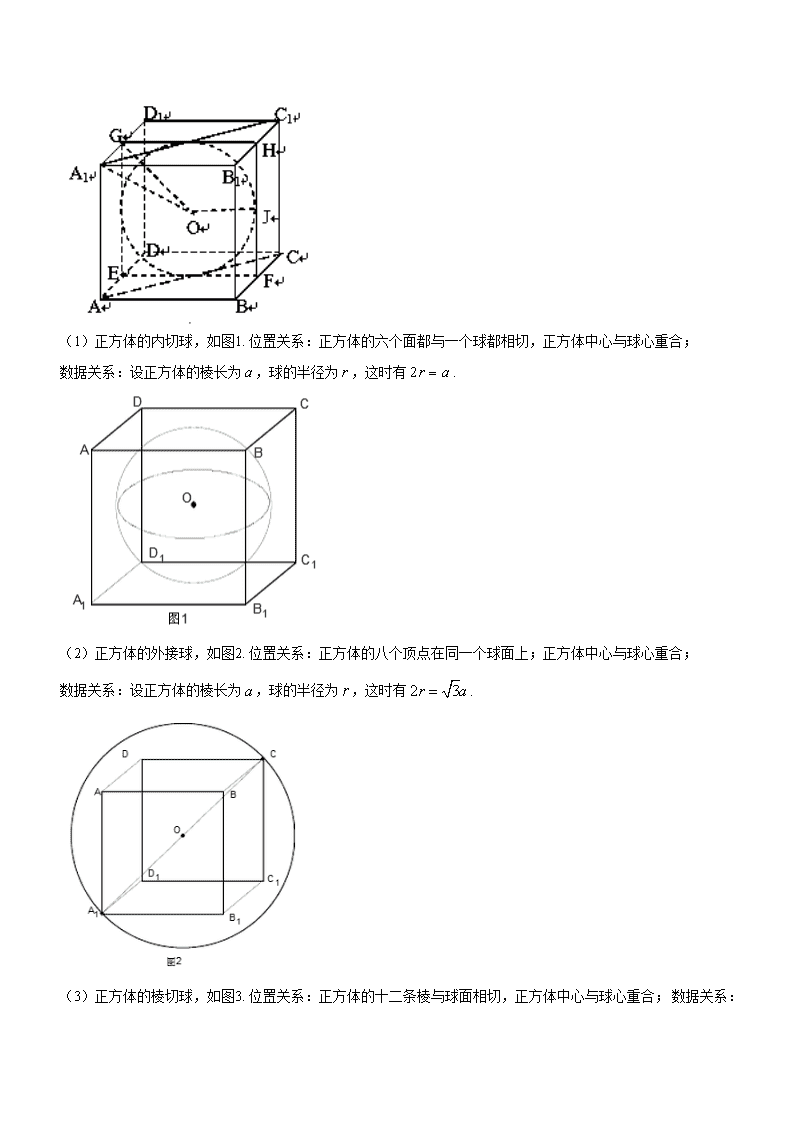
热点七 几何体与球切、接的问题 ‎ 纵观近几年高考对于组合体的考查，与球相关的外接与内切问题是高考命题的热点之一.高考命题小题综合化倾向尤为明显，要求学生有较强的空间想象能力和准确的计算能力，才能顺利解答.从实际教学来看，这部分知识学生掌握较为薄弱、认识较为模糊，看到就头疼的题目.分析原因，除了这类题目的入手确实不易之外，主要是学生没有形成解题的模式和套路，以至于遇到类似的题目便产生畏惧心理. 下面结合近几年高考题对球与几何体的切接问题作深入的探究,以便更好地把握高考命题的趋势和高考的命题思路,力争在这部分内容不失分.从近几年全国高考命题来看,这部分内容以选择题、填空题为主，大题很少见. ‎ 首先明确定义1：若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球。‎ 定义2：若一个多面体的各面都与一个球的球面相切， 则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球.‎ ‎1 球与柱体的切接 ‎ 规则的柱体，如正方体、长方体、正棱柱等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱柱的棱产生联系，然后考查几何体的体积或者表面积等相关问题.‎ 1.1 ‎ 球与正方体 ‎ 如图所示，正方体，设正方体的棱长为，为棱的中点，为球的球心.常见组合方式有三类：一是球为正方体的内切球，截面图为正方形和其内切圆，则；二是与正方体各棱相切的球，截面图为正方形和其外接圆，则；三是球为正方体的外接球，截面图为长方形和其外接圆，则.通过这三种类型可以发现，解决正方体与球的组合问题，常用工具是截面图，即根据组合的形式找到两个几何体的轴截面，通过两个截面图的位置关系，确定好正方体的棱与球的半径的关系，进而将空间问题转化为平面问题.‎ ‎（1）正方体的内切球，如图1. 位置关系：正方体的六个面都与一个球都相切，正方体中心与球心重合； ‎ 数据关系：设正方体的棱长为，球的半径为，这时有. ‎ ‎（2）正方体的外接球，如图2. 位置关系：正方体的八个顶点在同一个球面上；正方体中心与球心重合； ‎ 数据关系：设正方体的棱长为，球的半径为，这时有.‎ ‎（3）正方体的棱切球，如图3. 位置关系：正方体的十二条棱与球面相切，正方体中心与球心重合； ‎ 数据关系：设正方体的棱长为，球的半径为，这时有.‎ 例 1【2018届福建省三明市A片区高中联盟校高三上学期期末】某几何体的三视图如图所示，则该几何体的外接球的表面积为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【针对练习】‎ ‎1.如图，虚线小方格是边长为1的正方形，粗实(虚)线画出的是某几何体的三视图，则该几何体外接球的表面积为 A．36π B． 32π C．9π D．8π 答案及解析：‎ ‎1.B 几何体的直观图如图所示为三棱锥，三棱锥中，‎ ‎，所以外接球的直径为，则半径，所以外接球的表面积,故选B.‎ ‎ ‎ 1.1 球与长方体 例 2 自半径为的球面上一点，引球的三条两两垂直的弦，求的值．‎ ‎【答案】.‎ ‎【解析】以为从一个顶点出发的三条棱，将三棱锥补成一个长方体，则另外四个顶点必在球面上，故长方体是球的内接长方体，则长方体的对角线长是球的直径． ‎ ‎=．‎ 例 3【2018届二轮复习专题】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥PABC为鳖臑，PA⊥平面ABC，PA＝AB＝2，AC＝4，三棱锥PABC的四个顶点都在球O的球面上，则球O的表面积为(　　)‎ A. 8π B. 12π C. 20π D. 24π ‎【答案】C ‎【针对练习】 1.已知边长为2的等边三角形ABC，D为BC的中点，以AD为折痕，将△ABC折成直二面角，则过A，B，C，D四点的球的表面积为 A. 2π B. 3π C. 4π 　 D. 5π ‎ 答案及解析：‎ ‎1.D折后的图形可放到一个长方体中，其体对角线长为， 故其外接球的半径为，其表面积为.故选D.‎ ‎2 球与锥体的切接 ‎ 规则的锥体，如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱锥的棱和高产生联系，然后考查几何体的体积或者表面积等相关问题.‎ ‎2.1正四面体与球的切接问题 ‎ ‎ ‎ ‎ （1） 正四面体的内切球，如图4. 位置关系：正四面体的四个面都与一个球相切，正四面体的中心与球心重合； ‎ ‎ 数据关系：设正四面体的棱长为，高为；球的半径为，这时有；（可以利用体积桥证明） ‎ ‎ （2） 正四面体的外接球，如图5. 位置关系：正四面体的四个顶点都在一个球面上，正四面体的中心与球心重合； ‎ ‎ 数据关系：设正四面体的棱长为，高为；球的半径为，这时有；（可用正四面体高减去内切球的半径得到）‎ ‎ ‎ ‎ （3） 正四面体的棱切球，如图6. 位置关系：正四面体的六条棱与球面相切，正四面体的中心与球心重合； ‎ ‎ 数据关系：设正四面体的棱长为，高为；球的半径为，这时有 ‎ 例 4【2018届广西防城港市高三1月模拟】各面均为等边三角形的四面体的外接球的表面积为，过棱作球的截面，则截面面积的最小值为__________．‎ ‎【答案】‎ ‎【解析】将四面体放回一个正方体中,使正四面体的棱都是正方体的面对角线,那么正四面体和正方体的外接球是同一个球,当AB是截面圆的直径时,截面面积最小.‎ 因外接球的表面积为,则球的直径为,则正方体的体对角线为,棱长为1,面对角线为,截面圆面积最小值为.‎ 点评：与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图.‎ ‎【针对练习】 ‎ ‎1.设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为，则三棱锥D-ABC体积的最大值为 （ ）‎ ‎ A. B. C. D. ‎ 答案及解析：‎ ‎1.C ‎2.在四面体ABCD中，，则四面体体积最大时，它的外接球半径R= ．‎ 答案及解析：‎ ‎2.‎ 如图，‎ 取AB中点E，连接CE，DE，‎ 设AB=2x（0＜x＜1），则CE=DE=，‎ ‎∴当平面ABC⊥平面ABD时，四面体体积最大，‎ 为V===．‎ V′=，当x∈（0，）时，V为增函数，当x∈（，1）时，V为减函数，‎ 则当x=时，V有最大值．‎ 设△ABD的外心为G，△ABC的外心为H，‎ 分别过G、H作平面ABD、平面ABC的垂线交于O，则O为四面体ABCD的外接球的球心．‎ 在△ABD中，有sin，则cos，‎ ‎∴sin=．‎ 设△ABD的外接圆的半径为r，则，即DG=r=．‎ 又DE=，∴OG=HE=GE=．‎ ‎∴它的外接球半径R=OD=．‎ ‎2.2其它棱锥与球的切接问题 ‎ ‎ ‎ 球与正棱锥的组合，常见的有两类，一是球为三棱锥的外接球，此时三棱锥的各个顶点在球面上，根据截面图的特点，可以构造直角三角形进行求解.二是球为正棱锥的内切球，例如正三棱锥的内切球，球与正三棱锥四个面相切，球心到四个面的距离相等，都为球半径．这样求球的半径可转化为球球心到三棱锥面的距离，故可采用等体积法解决，即四个小三棱锥的体积和为正三棱锥的体积.‎ ‎ 球与一些特殊的棱锥进行组合，一定要抓住棱锥的几何性质，可综合利用截面法、补形法等进行求解.例如，四个面都是直角三角形的三棱锥，可利用直角三角形斜边中点几何特征，巧定球心位置.‎ 例5【湖南省长沙市长郡中学2017届高三摸底】已知边长为的菱形中，，沿对角线折成二面角为的四面体，则四面体的外接球的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】D 例6【江西省新余市第一中学2017届高三上学期调研考试（一）】某几何体的正视图和侧视图如图（1）所示, 它的府视图的直观图是,如图（2）所示, 其中,则该几何体的外接球的表面积为 ．‎ ‎ ‎ ‎【答案】‎ ‎【解析】‎ 由斜二测画法易知，该几何体的俯视图是一个边长为4的等边三角形,再结合正视图和侧视图可知，该几何体是如下图所示的高为4的三棱锥D－ABC，将其补形为三棱柱ABC-EDF,设球心为O，的中心为，则,所以该几何体的外接球的半径,其表面积为.‎ 例7【2018届山西省太原十二中高三上学期1月】在四棱锥中， 底面，底面为正方形， ， ，记四棱锥的外接球与三棱锥的外接球的表面积分别为，则___．‎ ‎【答案】‎ ‎【解析】设正方形的边长为，设为的中点，因为平面，而平面 ‎，所以，又，故，又，故平面， 平面，所以，故为直角三角形， 为斜边，所以．同理也为直角三角形，结合 ，所以，又， ，所以平面， 平面，所以， 为直角三角形，所以， 为三棱锥 外接球的球心，且半径．同理设为的中点，则为四棱锥外接球的球心，且半径，所以．填．‎ 点睛：球的半径的计算，关键在球心位置的确定，三棱锥中均为直角三角形，因此外接球的球心就是的中点，因为它到四个顶点的距离是相等的．同理四棱锥外接球的球心就是的中点．‎ ‎【针对练习】 1.已知在三棱锥P-ABC中，，，，平面PAB⊥平面ABC，若三棱锥的顶点在同一个球面上，则该球的表面积为（ ）‎ A． B． C． D．‎ 答案及解析：‎ ‎1.B试题分析：如下图所示，设球心为，则可知球心在面的投影在外心，即中点处，取中点，连，，，，由题意得，面，∴在四边形中，设，∴半径，，即球心即为中点，∴表面积，故选B.‎ ‎2.在四面体S﹣ABC中，SA⊥平面ABC，∠BAC=120°，SA=AC=2，AB=1，则该四面体的外接球的表面积为 A．11π B． C． D．‎ 答案及解析：‎ ‎2.D ∵AC=2，AB=1，∠BAC=120°，‎ ‎∴BC= ，‎ ‎∴三角形ABC的外接圆半径为r，2r= ，r= ，‎ ‎∵SA⊥平面ABC，SA=2，‎ 由于三角形OSA为等腰三角形，O是外接球的球心．‎ 则有该三棱锥的外接球的半径R= ，‎ ‎∴该三棱锥的外接球的表面积为S=4πR2= ．‎ 选D.‎ ‎3.在四面体ABCD中，△BCD与△ACD均是边长为4的等边三角形，二面角A-CD-B的大小为60°，则四面体ABCD外接球的表面积为（ ）‎ A． B． C． D．‎ 答案及解析：‎ ‎3.A 根据题意得到这个模型是两个全等的三角形，二面角大小为，取CD的中点记为O，连结OB，OA，根据题意需要找到外接球的球心，选择OA的离O点近的3等分店记为E，同理去OB上一点记为F，自这两点分别做两个面的垂线，交于点P，则点P就是球心。在三角形POE中，角POE为三十度，OE= ‎ 故答案为：A.‎ ‎4.已知在三棱锥 A - BCD中，，，底面BCD为等边三角形，且平面ABD⊥平面BCD，则三棱锥A - BCD外接球的表面积为 ．‎ 答案及解析：‎ ‎4.16π 取BD的中点E，连接AE，CE，取CE的三等分点为O，使得CO=2OE，则O为等边△BCD的中心.由于平面ABD⊥平面BCD，且平面ABD∩平面BCD=BD，CE⊥BD，所以平面ACE⊥平面ABD.由于AB2+AD2=BD2，所以△ABD为直角三角形，且E为△ABD的外心，所以OA=OB=OD.又OB=OC=OD，所以O为三棱锥A-BCD外接球的球心，且球的半径 ‎.故三棱锥A-BCD外接球的表面积为.‎ ‎3 球与球相切问题 ‎ 对于球与球的相切组合成复杂的几何体问题，要根据丰富的空间想象力，通过准确确定各个小球的球心的位置，或者巧借截面图等方法，将空间问题转化平面问题求解.‎ 例8 已知有半径分别为2、3的球各两个，且这四个球彼此相外切，现有一个球与此四个球都相外切，则此球 的半径为 .‎ ‎【答案】‎ ‎【解析】如图：设四个球的球心分别为A、B、C、D，则AD=AC=BD=BC=5，AB=6，CD=4.设AB中点为E、‎ CD中点为F，连结EF.在△ABF中求得BF=，在△EBF中求得EF=.‎ 由于对称性可得第五个球的球心O在EF上，连结OA、OD.设第五个球的半径为r，则OA=r+3，OD=r+2， ‎ 于是OE=，OF=，∵OE+OF=EF ‎∴平方整理再平方得 解得或（舍掉），故答案为.‎ 例9 把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与 前三个都相切，求第四个球的最高点与桌面的距离．‎ ‎【答案】.‎ ‎【针对练习】 1.两球和在棱长为1的正方体的内部，且互相外切，若球与过点的正方体的三个面相切，球与过点的正方体的三个面相切，则球和的表面积之和的最小值为( )‎ A． B． C. D．‎ 答案及解析：‎ ‎1.A ‎4球与几何体的各条棱相切问题 ‎ 球与几何体的各条棱相切问题，关键要抓住棱与球相切的几何性质，达到明确球心的位置为目的，然后通过构造直角三角形进行转换和求解.如与正四面体各棱都相切的球的半径为相对棱的一半：.‎ 例10 把一个皮球放入如图10所示的由8根长均为20 cm的铁丝接成的四棱锥形骨架内，使皮球的表面与 ‎8根铁丝都有接触点，则皮球的半径为（ ）‎ A．l0cm B．10 cm C．10cm D．30cm ‎【答案】‎ ‎【解析】如图所示，由题意球心在AP上，球心为O，过O作BP的垂线ON垂足为N，ON=R，OM=R，因为各个棱都为20，所以AM=10，BP=20,BM=10，AB=,设，‎ 在BPM中，,所以.在PAM中, ,所以 ‎.在ABP中, ，在ONP中, ,所以 ‎，所以.在OAM中, ,所以，‎ ‎,解得，或30（舍）,所以，故选B.‎ ‎ ‎ 4 球与旋转体切接问题 ‎ 首先画出球及其它旋转体的公共轴截面，然后寻找几何体与几何体几何元素之间的关系．‎ 例11 求球与它的外切圆柱、外切等边圆锥的体积之比．‎ ‎【答案】‎ ‎【解析】如图，等边为圆锥的轴截面，此截面截圆柱得正方形，截球面得球的大圆圆．‎ ‎ 设球的半径，则它的外切圆柱的高为，底面半径为；‎ ‎， ，‎ ‎∴，， ，‎ ‎∴．‎ ‎ ‎ 例12在棱长为1的正方体内有两个球相外切且又分别与正方体内切．（1）求两球半径之和；（2）球的半径 为多少时，两球体积之和最小．‎ ‎【答案】‎ ‎【解析】如图，球心和在上，过，分别作的垂线交于．‎ 则由得．‎ ‎， ．‎ ‎ ‎ ‎【反思提升】综合上面的五种类型，解决与球的外切问题主要是指球外切多面体与旋转体，解答时首先要找准切点，将问题转化成平面几何问题，应用三角形中的边角关系，建立与球半径的联系，将球的体积之和用或表示.如果外切的是多面体，则作截面时主要抓住多面体过球心的对角面来作；把一个多面体的几个顶点放在球面上即为球的内接问题．解决这类问题的关键是抓住内接的特点，即球心到多面体的顶点的距离等于球的半径．发挥好空间想象力，借助于数形结合进行转化，问题即可得解．如果是一些特殊的几何体，如正方体、正四面体等可以借助结论直接求解,此时结论的记忆必须准确.高考题往往与三视图相结合，题目的难易不一，在复习中切忌好高骛远，应重视各种题型的备考演练，重视高考信息的搜集，不断充实题目的类型，升华解题的境界.‎ ‎【针对练习】‎ ‎1.已知四棱锥S—ABCD，SA⊥平面ABCD，AB⊥BC，∠BCD＋∠DAB＝π，SA＝2，，二面角S—BC—A的大小为．若四面体SACD的四个顶点都在同一球面上，则该球的表面积为 A． B．4π C．8π D．16π 答案及解析：‎ ‎10.C ‎2.已知三棱柱ABC-A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为 ‎,则此球的体积等于(   )‎ A.B.C.D.‎ 答案及解析：‎ ‎19.B ‎3.‎ 在四面体ABCD中，AD⊥底面ABC，，BC=2，E为棱BC的中点，点G在AE上且满足AG=2GE，若四面体ABCD的外接球的表面积为，则（ ）‎ A． B． C． D．2‎ 答案及解析：‎ ‎3.D 设△ABC的外心为O，则点O在AE上，设OE=r,则.‎ 设四面体ABCD的外接球半径为R，则.‎ 因为 所以. 故选D.‎ ‎4.《九章算术》是我国古代数学名著，它在几何学中的研究比西方早一千多年，其中有很多对几何体外接球的研究，如下图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的外接球的体积是（ ）‎ A．81π B．33π C. 56π D．41π 答案及解析：‎ ‎4.D 由三视图可得，该几何体是一个如图所示的四棱锥，其中是边长为4的正方形，平面平面．‎ ‎ ‎ 设为的中点，为正方形的中心，为四棱锥外接球的球心，为外接圆的圆心，则球心为过点且与平面垂直的直线与过且与平面垂直的直线的交点．‎ 由于为钝角三角形，故在的外部，从而球心与点P在平面的两侧．‎ 由题意得，‎ 设球半径为，则,‎ 即，解得，‎ ‎∴，‎ ‎∴．选D．‎ ‎5.正三棱柱的顶点都在同一个球面上，若球的半径为4，则该三棱柱的侧面面积的最大值为 （ ）‎ ‎（A） （B） （C） （D）‎ 答案及解析：‎ ‎5.A 设正三棱柱高为h，底面正三角形边长为a，则三棱柱侧面面积为 ，因为 ，所以 因此三棱柱侧面面积最大值为 ，选A ‎6.四棱锥P - ABCD的底面ABCD为正方形，PA⊥底面ABCD，AB=2，若该四棱锥的所有顶点都在体积为的同一球面上，则PA=（　 ）‎ ‎（A）3　　　（B）　　　（C）　　　　（D）‎ 答案及解析：‎ ‎6.B 试题分析：连结交于点，取的中点，连结，则，所以底面，则到四棱锥的所有顶点的距离相等，即为球心，半径为,所以球的体积为，解得，故选B．‎ ‎7.某棱锥的三视图如下图所示,则该棱锥的外接球的表面积为（ ）‎ A．11π B．12π C. 13π D．14π 答案及解析：‎ ‎7.A 由三视图可知该几何体是如图所示的三棱锥，‎ 外接球球心在过中点且垂直于平面的直线上，‎ 又点到距离相等，∴点又在线段的垂直平分面上，‎ 故是直线与面的交点，可知是直线与直线的交点 ‎（分别是左侧正方体对棱的中点）‎ ‎∴，， ‎ 故三棱锥外接球的半径，表面积为 ‎8.下图是某四棱锥的三视图，网格纸上小正方形的边长为1，则该四棱锥的外接球的表面积为（ ）‎ A． B． C. 41π D．31π 答案及解析：‎ ‎8.C 根据三视图得出：该几何体是镶嵌在正方体中的四棱锥O﹣ABCD，正方体的棱长为2，‎ A，D为棱的中点 其中.‎ 根据几何体可以判断：球心应该在过A，D的平行于底面的中截面上，‎ 设球心到截面BCO的距离为x，则到AD的距离为：4﹣x，‎ ‎∴R2=x2+（）2，R2=22+（4﹣x）2，‎ 解得出：，‎ 该多面体外接球的表面积为：4πR2=，‎ 故选：C．‎ ‎9.三棱锥P-ABC中，底面ABC满足，，点P在底面ABC的射影为AC的中点，且该三棱锥的体积为，当其外接球的表面积最小时，P到底面ABC的距离为 .‎ 答案及解析：‎ ‎9.‎ ‎67.‎ 在三棱锥P-ABC中，,,,,则该三棱锥的外接球的表面积为 ‎ 答案及解析：‎ ‎67.5π ‎ ‎68.‎ 在四面体ABCD中，若AB=CD=，AC=BD=2，AD=BC=，则四面体ABCD的外接球的表面积为__________．‎ 答案及解析：‎ ‎68. 6π ‎69.‎ 已知三棱锥均为等边三角形，二面角的平面角为60°，则三棱锥外接球的表面积是 .‎ ‎81.‎ 表面积为的球面上有四点，，，，且为等边三角形，球心到平面的距离为，若平面平面，则三棱锥的体积的最大值为 ．‎ 答案及解析：‎ ‎81.‎ 过O作OF⊥平面SAB,则F为△SAB的中心,过F作FE⊥SA于E点,则E为SA中点,‎ 取AB中点D,连结SD,则∠ASD=30∘，设球O半径为r,则,解得.‎ 连结OS,则 ‎.‎ 过O作OM⊥平面ABC，则当C，M，D三点共线时，C到平面SAB的距离最大，即三棱锥S−ABC体积最大.‎ 连结OC，∵平面SAB⊥平面ABC，∴四边形OMDF是矩形，‎ ‎∴三棱锥S−ABC体积.‎ 点睛：‎ 求三棱锥的体积时要注意三棱锥的每个面都可以作为底面，例如三棱锥的三条侧棱两两垂直，我们就选择其中的一个侧面作为底面，另一条侧棱作为高来求体积．与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，‎ ‎83.‎ 已知三棱锥中，，当三棱锥的体积最大时，其外接球的体积为 ． ‎ 答案及解析：‎ ‎83.‎ 当平面时，三棱锥的体积最大，‎ 由于，‎ ‎，则为直角三角形，‎ 三棱锥的外接球就是以为棱的长方体的外接球，‎ 长方体的对角线等于外接球的直径，‎ 设外接球的半径为，‎ 则，解得，‎ 球体的体积为，故答案为.‎ ‎87.‎ 在三棱锥中，,,PA与平面ABC所成角的余弦值为，则三棱锥P - ABC外接球的表面积为 ．‎ 答案及解析：‎ ‎87.12π ‎89.‎ 在几何体中，是正三角形，平面平面，且，，则的外接球的表面积等于 ．‎ 答案及解析：‎ ‎89.‎ ‎ ‎ 由题意，取AB,PB的中点E,F，连接AF,PE，且 ，则点M为正三角形PAB的中点， ，易证PE ⊥平面ABC，取AC中点D，连接ED，‎ 作OD∥PE，OM∥ED，连接OA，则OA为外接球的半径，又 ， ，则 ，‎ 所以外接球的表面积为 ，从而问题可得解.‎ ‎91.‎ 已知一个四面体的每个顶点都在表面积为的球的表面积，且，，则 ．‎ 答案及解析：‎ ‎91.‎ ‎98.‎ 矩形中，，，平面，，，分别是，的中点，则四棱锥的外接球表面积为 ．‎ 答案及解析：‎ ‎98.‎ ‎99.‎ 某艺术品公司欲生产一款迎新春工艺礼品，该礼品是由玻璃球面和该球的内接圆锥组成，圆锥的侧面用于艺术装饰，如图1.为了便于设计，可将该礼品看成是由圆O及其内接等腰三角形ABC绕底边BC上的高所在直线AO旋转180°而成，如图2.已知圆O的半径为10cm，设，圆锥的侧面积为Scm2.‎ ‎（1）求S关于的函数关系式；‎ ‎（2）为了达到最佳观赏效果，要求圆锥的侧面积S最大.求S取得最大值时腰AB的长度.‎ 答案及解析：‎ ‎99.‎ ‎（1）设交于点，过作，垂足为， ‎ 在中，，，‎ 在中，，‎ 所以 ‎， ‎ ‎（2）要使侧面积最大，由（1）得：‎ ‎ ‎ 设 ‎ 则，由得：‎ 当时，，当时，‎ 所以在区间上单调递增，在区间上单调递减，‎ 所以在时取得极大值，也是最大值；‎ 所以当时，侧面积取得最大值， ‎ 此时等腰三角形的腰长 答：侧面积取得最大值时，等腰三角形的腰的长度为 ‎ ‎100.‎ 如图，在四面体ABCD中，平面ABC⊥平面BCD，DC⊥BC，AB=，BC=2，AC=1．‎ ‎（1）求证：AB⊥AD；‎ ‎（2）设E是BD的中点，若直线CE与平面ACD的夹角为30°，求四面体ABCD外接球的表面积．‎ 答案及解析：‎ ‎100.‎ ‎【分析】（1）证明DC⊥BC，AB⊥CD，推出AB⊥AC，然后证明AB⊥平面ADC，得到AB⊥AD．‎ ‎（2）取AD的中点F，连接EF，则EF∥BA，证明EF⊥平面ADC，连接FC，说明∠ECF=30°，求出以四面体ABCD的外接球的半径然后求解即可．‎ ‎【解答】解：（1）证明：由平面ABC⊥平面BCD，DC⊥BC，得DC⊥平面ABC，∴AB⊥CD…（2分）‎ 又由，BC=2，AC=1，得BC2=AB2+AC2，所以AB⊥AC…（4分）‎ 故AB⊥平面ADC，所以AB⊥AD…（6分）‎ ‎（2）取AD的中点F，连接EF，则EF∥BA，‎ 因为AB⊥平面ADC∴EF⊥平面ADC…（8分）‎ 连接FC，则∠ECF=30°，∴…（9分）‎ 又∠BAD=∠BCD=90°，‎ 所以四面体ABCD的外接球的半径…（11分）‎ 故四面体ABCD的外接球的表面积=…（12分）‎ ‎（向量解法酌情给分）‎ ‎【点评】本题考查直线与平面垂直的判定定理的应用，几何体的外接球的表面积的求法，直线与平面所成角的应用，考查空间想象能力以及计算能力．‎