新课标2007-2013高考真题数学理
2007 年普通高等学校招生全国统一考试
理科数学(宁夏、 海南卷)
本试卷分第 I 卷(选择题)和第 II 卷(非选择题)两部分.第 II 卷第 22 题为选考题,其他题为必考题.考
生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回.
注意事项:
1.答题前,考生先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的
准考证号、姓名,并将条形码粘贴在指定位置上.
2.选择题答案使用 2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案
使用 0.5 毫米的黑色中性(签字)笔或炭素笔书写,字体工整,笔迹清楚.
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.
4.保持卡面清洁,不折叠,不破损.
5.作选考题时,考生按照题目要求作答,并用 2B 铅笔在答题卡上把所选题目对应的标号涂黑.
参考公式:
样本数据 1x , 2x ,, nx 的标准差 锥体体积公式
2 2 2
1 2
1 [( ) ( ) ( ) ]ns x x x x x x
n
1
3
V Sh
其中 x为样本平均数 其中 S为底面面积、 h为高
柱体体积公式 球的表面积、体积公式
V Sh 24πS R ,
34 π
3
V R
其中 S为底面面积, h为高 其中 R为球的半径
第 I卷
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.已知命题 :p x R , sin 1x≤ ,则( )
A. :p x R , sin 1x≥ B. :p x R , sin 1x≥
C. :p x R , sin 1x D. :p x R , sin 1x
【解析】 p 是对 p的否定,故有: ,x R sin 1.x
答案:C
2.已知平面向量 (11) (1 1) ,, ,a b ,则向量
1 3
2 2
a b ( )
A. ( 2 1) , B. ( 2 1) ,
C. ( 1 0) , D. ( 1 2) ,
【解析】
1 3
2 2
a b ( 1 2). ,
答案:D
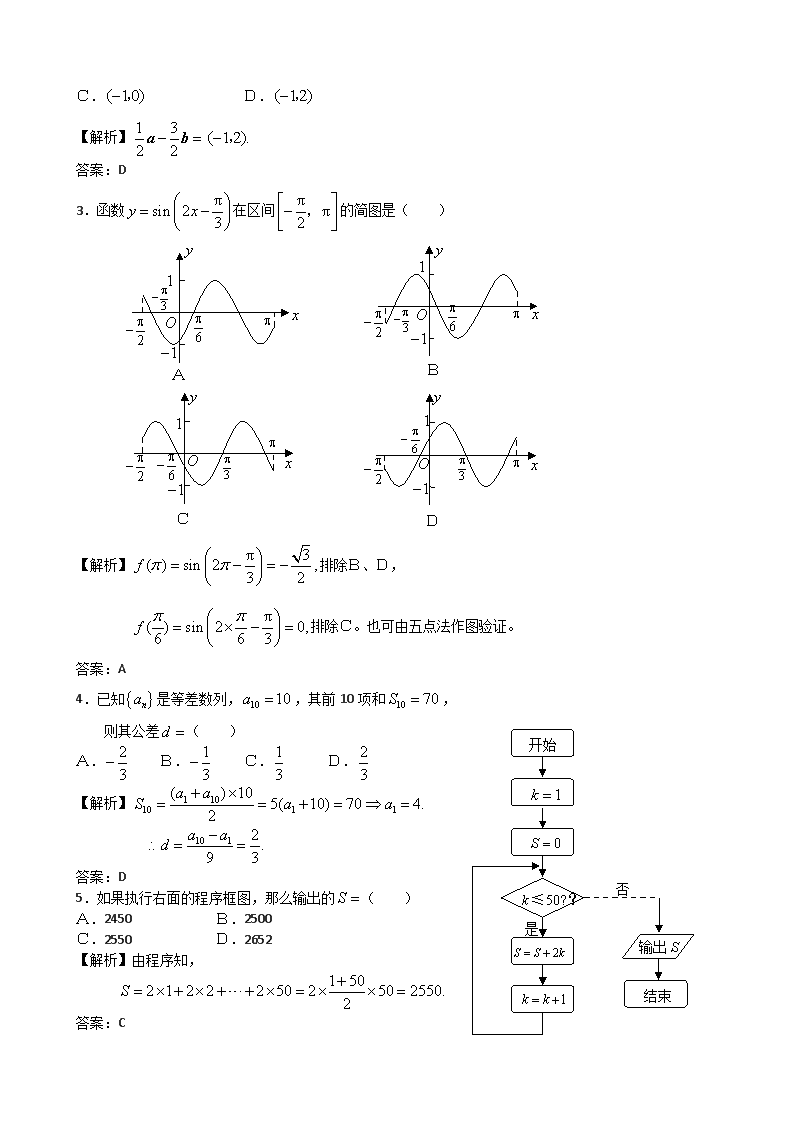
3.函数
πsin 2
3
y x
在区间
π π
2
, 的简图是( )
【解析】
π 3( ) sin 2 ,
3 2
f
排除B、D,
π( ) sin 2 0,
6 6 3
f
排除C。也可由五点法作图验证。
答案:A
4.已知 na 是等差数列, 10 10a ,其前 10 项和 10 70S ,
则其公差 d ( )
A.
2
3
B.
1
3
C.
1
3
D.
2
3
【解析】 1 10
10 1 1
( ) 10 5( 10) 70 4.
2
a aS a a
10 1 2 .
9 3
a ad
答案:D
5.如果执行右面的程序框图,那么输出的 S ( )
A.2450 B.2500
C.2550 D.2652
【解析】由程序知,
1 502 1 2 2 2 50 2 50 2550.
2
S
答案:C
6.已知抛物线
2 2 ( 0)y px p 的焦点为 F ,
y
x
1
1
2
3
O
6
y
x
1
12
3
O
6
y
x
1
1
2
3
O
6
y
x
2
6
1
O
1
3
A. B.
C. D.
开始
1k
0S
50?k≤
是
2S S k
1k k
否
输出 S
结束
�
P
D C
BA
点 1 1 1 2 2 2( ) ( )P x y P x y, , , , 3 3 3( )P x y, 在抛物线上,
且 2 1 32x x x , 则有( )
A. 1 2 3FP FP FP B.
2 2 2
1 2 3FP FP FP
C. 2 1 32 FP FP FP D.
2
2 1 3FP FP FP ·
【解析】由抛物线定义,
2 1 32( ) ( ) ( ),
2 2 2
p p px x x 即: 2 1 32 FP FP FP .
答案:C
7.已知 0x , 0y , x a b y, , , 成等差数列, x c d y, , , 成等比数列,
则
2( )a b
cd
的最小值是( )
A. 0 B.1 C. 2 D. 4
【解析】 , ,a b x y cd xy
22 2 (2 )( ) ( ) 4.
xya b x y
cd xy xy
答案:D
8.已知某个几何体的三视图如下,根据图中
标出 的尺寸(单位:cm),可得这个几
何体的体积是( )
A.
34000 cm
3
B.
38000 cm
3
C.
32000cm
D.
34000cm
【解析】如图,
1 800020 20 20 .
3 3
V
答案:B
9.若
cos 2 2
π 2sin
4
,则 cos sin 的值为( )
A.
7
2
B.
1
2
C.
1
2
D.
7
2
20
20
正视图
20
侧视图
10
10
20
俯视图
【解析】
2 2cos 2 cos sin 22(sin cos ) ,
π 22sin (sin cos )4 2
1cos sin .
2
答案:C
10.曲线
1
2e
x
y 在点
2(4 e ), 处的切线与坐标轴所围三角形的面积为( )
A.
29 e
2
B.
24e C.
22e D.
2e
【 解 析 】
1 1
2 21( ) ,
2
x x
y e e 曲 线 在 点
2(4 e ), 处 的 切 线 斜 率 为
21
2
e , 因 此 切 线 方 程 为
2 21 ( 4),
2
y e e x 则切线与坐标轴交点为
2(2,0), (0, ),A B e 所以:
2 21 | | 2 .
2AOBS e e
答案:D
11.甲、乙、丙三名射箭运动员在某次测试中各射箭 20 次,三人的测试成绩如下表
1 2 3s s s, , 分 别 表示甲、乙、丙
三名运动员这次测试成绩的标准差,则有( )
A. 3 1 2s s s B. 2 1 3s s s
C. 1 2 3s s s D. 2 3 1s s s
【解析】
(7 8 9 10) 5 8.5,
20
x
甲
2 2 2 2
2
1
5 [(7 8.5) (8 8.5) (9 8.5) (10 8.5) ] 1.25,
20
s
(7 10) 6 (8 9) 4 8.5,
20
x
乙
2 2 2 2
2
2
6 [(7 8.5) (10 8.5) ] 4 [(8 8.5) (9 8.5) ] 1.45,
20
s
(7 10) 4 (8 9) 6 8.5,
20
x
丙
2 2 2 2
2
3
4 [(7 8.5) (10 8.5) ] 6 [(8 8.5) (9 8.5) ] 1.05,
20
s
2 2
2 1 3 2 1 3 .s s s s s s 2由 得
甲的成绩
环数 7 8 9
1
0
频数 5 5 5 5
乙的成绩
环数 7 8 9
1
0
频数 6 4 4 6
丙的成绩
环数 7 8 9
1
0
频数 4 6 6 4
�
h
�
1
h(h2)
P
D
C
B
A
E
答案:B
12.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形,
且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、
三棱锥、三棱柱的高分别为 1h , 2h , h,则 1 2: :h h h ( )
A. 3 :1:1 B. 3 : 2 : 2 C. 3 : 2 : 2 D. 3 : 2 : 3
【解析】如图,设正三棱锥 P ABE 的各棱长为a,
则四棱锥 P ABCD 的各棱长也为 a,
于是
2 2
1
2 2( ) ,
2 2
h a a a
2 2
2
3 2 6( ) ,
2 3 2
h a a a h
1 2: : 3 : 2 : 2.h h h
答案:B
第 II卷
本卷包括必考题和选考题两部分,第 13 题-第 21 题为必考题,每个试题考生都必须做答,第 22 题
为选考题,考生根据要求做答.
二、填空题:本大题共 4 小题,每小题 5 分.
13.已知双曲线的顶点到渐近线的距离为 2,焦点到渐近线
的距离为 6,则该双曲线的离心率为 .
【解析】如图,过双曲线的顶点 A、焦点 F 分别
向其渐近线作垂线,垂足分别为 B、C,
则:
| | | | 6 3.
| | | | 2
OF FC c
OA AB a
答案:3
14.设函数
( 1)( )( ) x x af x
x
为奇函数,则 a .
【解析】 (1) ( 1) 0 2(1 ) 0 0, 1.f f a a
答案:-1
15. i是虚数单位,
5 10
3 4
i
i
.(用 a bi 的形式表示, a bR, )
【解析】
5 10 ( 5 10 )(3 4 ) 25 50 1 2 .
3 4 (3 4 )(3 4 ) 25
i i i i i
i i i
答案:1 2i
16.某校安排 5 个班到 4 个工厂进行社会实践,每个班去一个工厂,每个工厂至少安排
一个班,不同的安排方法共有 种.(用数字作答)
【解析】由题意可知有一个工厂安排 2 个班,另外三个工厂每厂一个班,
共有
1 2 3
4 5 3 240.C C A 种安排方法。
答案:240
三、解答题:解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分 12 分)
如图,测量河对岸的塔高 AB时,可以选与塔底 B在同一水平面
内的两个测点C与D.现测得 BCD BDC CD s , , ,
并在点C测得塔顶 A的仰角为 ,求塔高 AB.
【解析】在 BCD△ 中, πCBD .
由正弦定理得
sin sin
BC CD
BDC CBD
.
所以
sin sin
sin sin( )
CD BDC sBC
CBD
.
在 ABCRt△ 中,
tan sintan
sin( )
sAB BC ACB
.
18.(本小题满分 12 分)
如图,在三棱锥 S ABC 中,侧面 SAB与侧面 SAC
均为等边三角形, 90BAC °,O为 BC中点.
(Ⅰ)证明: SO 平面 ABC;
(Ⅱ)求二面角 A SC B 的余弦值.
【解析】(Ⅰ)证明:
由题设 AB AC SB SC= = = SA,连结OA,
ABC△ 为等腰直角三角形,
所以
2
2
OA OB OC SA ,且 AO BC ,
又 SBC△ 为等腰三角形,故 SO BC ,
且
2
2
SO SA ,从而
2 2 2OA SO SA .
所以 SOA△ 为直角三角形, SO AO .
又 AO BO O .
所以 SO 平面 ABC.
(Ⅱ)解法一:
O
S
B A
C
O
S
B A
C
M
取 SC中点M ,连结 AM OM, ,由(Ⅰ)知 SO OC SA AC , ,
得OM SC AM SC , .
OMA∴ 为二面角 A SC B 的平面角.
由 AO BC AO SO SO BC O , , 得 AO 平面 SBC.
所以 AO OM ,又
3
2
AM SA ,
故
2 6sin
33
AOAMO
AM
.
所以二面角 A SC B 的余弦值为
3
3
.
解法二:
以O为坐标原点,射线OB OA, 分别为 x轴、 y轴的正半轴,
建立如图的空间直角坐标系O xyz .
设 (1 0 0)B ,, ,则 ( 1 0 0) (0 1 0) (0 0 1)C A S ,,, ,,, ,,.
SC的中点
1 10
2 2
M
,, ,
1 1 1 10 1 ( 1 0 1)
2 2 2 2
MO MA SC
,, , ,, , ,, .
0 0MO SC MA SC
,∴ · · .
故 ,MO SC MA SC MO MA
, ,< 等于
二面角 A SC B 的平面角.
3cos
3
MO MAMOMA
MO MA
,
·
·
,
所以二面角 A SC B 的余弦值为
3
3
.
19.(本小题满分 12 分)
在平面直角坐标系 xOy中,经过点 (0 2), 且斜率为 k的直线 l与椭圆
2
2 1
2
x y
有两个不同的交点 P和Q.
(I)求 k的取值范围;
(II)设椭圆与 x轴正半轴、 y轴正半轴的交点分别为 A B, ,是否存在常数 k,
O
S
B A
C
M
x
z
y
使得向量OP OQ
与 AB
共线?如果存在,求 k值;如果不存在,请说明理由.
【解析】(Ⅰ)由已知条件,直线 l的方程为 2y kx ,
代入椭圆方程得
2
2( 2) 1
2
x kx .
整理得
2 21 2 2 1 0
2
k x kx
①
直线 l与椭圆有两个不同的交点 P和Q等价于
2 2 218 4 4 2 0
2
k k k
,
解得
2
2
k 或
2
2
k .即 k的取值范围为
2 2
2 2
, ,∞ ∞ .
(Ⅱ)设 1 1 2 2( ) ( )P x y Q x y, , , ,则 1 2 1 2( )OP OQ x x y y
, ,
由方程①, 1 2 2
4 2
1 2
kx x
k
. ②
又 1 2 1 2( ) 2 2y y k x x . ③
而 ( 2 0) (0 1) ( 2 1)A B AB
,, ,, ,.
所以OP OQ
与 AB
共线等价于 1 2 1 22( )x x y y ,
将②③代入上式,解得
2
2
k .
由(Ⅰ)知
2
2
k 或
2
2
k ,故没有符合题意的常数 k.
20.(本小题满分 12 分)
如图,面积为 S 的正方形 ABCD中有一个不规则的图形M ,可按下面方法估计M 的面积:在正方形
ABCD中随机投掷 n个点,若 n个点中有m个点落入M 中,则M 的面积的估计值为
m S
n
. 假设正方形
ABCD的边长为 2,M 的面积为 1,并向正方形 ABCD中随机投掷10000个点,以 X 表示落入M 中的
点的数目.
(I)求 X 的均值 EX ;
(II)求用以上方法估计M 的面积时,M 的面积的估计值与实际 值 之 差
在区间 ( 0.03 ) , 内的概率.
D C
BA
M
附表:
10000
10000
0
( ) 0.25 0.75
k
t t t
t
P k C
k 2424 2425 2574 2575
( )P k 0.0403 0.0423 0.9570 0.9590
【解析】每个点落入M 中的概率均为
1
4
p .依题意知
1~ 10000
4
X B
, .
(Ⅰ)
110000 2500
4
EX .
(Ⅱ)依题意所求概率为 0.03 4 1 0.03
10000
XP
,
0.03 4 1 0.03 (2425 2575)
10000
XP P X
2574
10000
10000
2426
0.25 0.75t t t
t
C
2574 2425
10000 10000 1
10000 10000
2426 0
0.25 0.75 0.25 0.75t t t t t
t t
C C
0.9570 0.0423 0.9147 .
21.(本小题满分 12 分)
设函数
2( ) ln( )f x x a x
(I)若当 1x 时, ( )f x 取得极值,求 a的值,并讨论 ( )f x 的单调性;
(II)若 ( )f x 存在极值,求 a的取值范围,并证明所有极值之和大于
eln
2
.
【解析】(Ⅰ)
1( ) 2f x x
x a
,依题意有 ( 1) 0f ,故
3
2
a .
从而
22 3 1 (2 1)( 1)( ) 3 3
2 2
x x x xf x
x x
.
( )f x 的定义域为
3
2
,∞ ,当
3 1
2
x 时, ( ) 0f x ;
当
11
2
x 时, ( ) 0f x ;
当
1
2
x 时, ( ) 0f x .
从而, ( )f x 分别在区间
3 11
2 2
, , ,∞ 单调增加,在区间
11
2
, 单调减少.
(Ⅱ) ( )f x 的定义域为 ( )a ,∞ ,
22 2 1( ) x axf x
x a
.
方程
22 2 1 0x ax 的判别式
24 8a .
(ⅰ)若 0 ,即 2 2a ,在 ( )f x 的定义域内 ( ) 0f x ,故 ( )f x 的极值.
(ⅱ)若 0 ,则 2a 或 2a .
若 2a , ( 2 )x ,∞ ,
2( 2 1)( )
2
xf x
x
.
当
2
2
x 时, ( ) 0f x ,
当
2 22
2 2
x
, ,∞ 时,
( ) 0f x ,所以 ( )f x 无极值.
若 2a , ( 2 )x ,∞ ,
2( 2 1)( ) 0
2
xf x
x
, ( )f x 也无极值.
(ⅲ)若 0 ,即 2a 或 2a ,则
22 2 1 0x ax 有两个不同的实根
2
1
2
2
a ax
,
2
2
2
2
a ax
.
当 2a 时, 1 2x a x a , ,从而 ( )f x 有 ( )f x 的定义域内没有零点,
故 ( )f x 无极值.
当 2a 时, 1x a , 2x a , ( )f x 在 ( )f x 的定义域内有两个不同的零点,
由根值判别方法知 ( )f x 在 1 2x x x x , 取得极值.
综上, ( )f x 存在极值时, a的取值范围为 ( 2 ),∞ .
( )f x 的极值之和为
2 2 2
1 2 1 1 2 2
1( ) ( ) ln( ) ln( ) ln 1 1 ln 2 ln
2 2
ef x f x x a x x a x a .
22.请考生在 A B C, , 三题中任选一题作答,如果多做,则按所做的第一题记分.
作答时,用 2B 铅笔在答题卡上把所选题目对应的标号涂黑.
22.A(本小题满分 10 分)选修 4-1:几何证明选讲
如图,已知 AP是 O 的切线,P为切点, AC是
O 的割线,与 O 交于 B C, 两点,圆心O在
PAC 的内部,点M 是 BC的中点.
(Ⅰ)证明 A P O M, , , 四点共圆;
(Ⅱ)求 OAM APM 的大小.
【解析】(Ⅰ)证明:连结OP OM, .
因为 AP与 O 相切于点 P,所以OP AP .
因为M 是 O 的弦 BC的中点,所以OM BC .
于是 180OPA OMA °.
由圆心O在 PAC 的内部,可知四边形 APOM 的对角互补,所以 A P O M, , , 四点共圆.
(Ⅱ)解:由(Ⅰ)得 A P O M, , , 四点共圆,所以 OAM OPM .
由(Ⅰ)得OP AP .
由圆心O在 PAC 的内部,可知 90OPM APM °.
所以 90OAM APM °.
22.B(本小题满分 10 分)选修 4-4:坐标系与参数方程
1O 和 2O 的极坐标方程分别为 4cos 4sin , .
(Ⅰ)把 1O 和 2O 的极坐标方程化为直角坐标方程;
(Ⅱ)求经过 1O , 2O 交点的直线的直角坐标方程.
【解析】以极点为原点,极轴为 x轴正半轴,建立平面直角坐标系,
两坐标系中取相同的长度单位.
(Ⅰ) cosx , siny ,由 4cos 得
2 4 cos .
所以
2 2 4x y x .
即
2 2 4 0x y x 为 1O 的直角坐标方程.
同理
2 2 4 0x y y 为 2O 的直角坐标方程.
(Ⅱ)由
2 2
2 2
4 0
4 0
x y x
x y y
,
解得
1
1
0
0
x
y
,
,
2
2
2
2
x
y
.
A
P
O
M
C
B
A
P
O
M
C
B
即 1O , 2O 交于点 (0 0), 和 (2 2), .过交点的直线的直角坐标方程为 y x .
22.C(本小题满分 10 分)选修 4 5 ;不等式选讲
设函数 ( ) 2 1 4f x x x .
(I)解不等式 ( ) 2f x ;
(II)求函数 ( )y f x 的最小值.
【解析】(Ⅰ)令 2 1 4y x x ,则
15
2
13 3 4
2
5 4
x x
y x x
x x
,������ ,
,� ,
,����������� .
≤
≥
...............3 分
作出函数 2 1 4y x x 的图象,它与直线 2y 的交点为 ( 7 2) , 和
5 2
3
, .
所以 2 1 4 2x x 的解集为
5( 7)
3
x x
, , .
(Ⅱ)由函数 2 1 4y x x 的图像可知,
当
1
2
x 时, 2 1 4y x x 取得最小值
9
2
.
2008 年普通高等学校招生全国统一考试(宁夏卷)
理科数学
数学(理)试题头说明:
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第 22-24 题为选考题,其它
题为必考题.考生作答时,将答案答在答题卡上.在本试卷上答题无效.考试结束后,将本试卷和答题卡
一并交回.
注意事项:
1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,
并将条形码粘贴在答题卡的指定位置上.
1
2
O
2y
4 x
y
2.选择题答案使用 2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用
0.5 毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.
4.保持卡面清洁,不折叠,不破损.
5.做选考题时,考生按照题目要求作答,并用 2B 铅笔在答题卡上把所选题目对应的题号涂黑.
参考公式:
样本数据 x1,x2, …,xn的标准参 锥体体积公式
s= 2 2 2
1 2
1 ( ) ( ) ( )nx x x x x x
n
… V=
3
1
Sh
其中 x 为样本平均数 其中 S 为底面面积,h 为高
柱体体积公式 球的表面积、体积公式
V=Sh 24S R ,
34
3
V R
其中 S 为底面面积,h 为高 其中 R 为球的半径
第Ⅰ卷
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知函数 2sin( )( 0)y x )在区间 0 2, 的图像如下:
y
x2π
1
1
O
那么=( )
A.1 B.2 C.
2
1
D.
3
1
2.已知复数 1z i ,则
1
22
z
zz
=( )
A. 2i B. 2i C.2 D. 2
3.如果等腰三角形的周长是底边长的 5 倍,那么它的顶角的余弦值为( )
A.
18
5
B.
4
3
C.
2
3
D.
8
7
4.设等比数列 na 的公比 q=2,前 n项和为 Sn,则
2
4
a
S
=( )
A. 2 B. 4 C.
2
15
D.
2
17
5.右面的程序框图,如果输入三个实数 a,b,c,要求输出这三
个数中最大的数,那么在空白的判断框中,应该填入下面四个选
项中的( )
A. c x B. x c C. c b D.b c
开始
输入 a b c, ,
x a
b x
x b
x c
输出 x
是
是
否
否
6.已知 a1>a2>a3>0,则使得
2(1 ) 1( 1 2 3)ia x i ,, 都成立的 x 取值范围是( )
A.
1
10
a
, B.
1
20
a
, C.
3
10
a
, D.
3
20
a
,
7. 2
3 sin 70
2 cos 10
( )
A.
1
2
B.
2
2
C.2 D.
3
2
8.平面向量 a,b 共线的充要条件是( )
A.a,b 方向相同
B.a,b 两向量中至少有一个为零向量
C. R∃ , b a
D.存在不全为零的实数 1 , 2 , 1 2 0a b
9.甲、乙、丙 3 位志愿者安排在周一至周五的 5 天中参加某项志愿者活动,要求每人参加一天且每天至
多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有( )
A.20 种 B.30 种 C.40 种 D.60 种
10.由直线
1
2
x ,x=2,曲线
1y
x
及 x轴所围图形的面积为( )
A.
15
4
B.
17
4
C.
1 ln 2
2
D. 2ln 2
11.已知点 P 在抛物线
2 4y x 上,那么点 P 到点 (2 1)Q , 的距离与点 P 到抛物线焦点距离之和取得最小
值时,点 P 的坐标为( )
A.
1 1
4
, B.
1 1
4
, C. (1 2), D. (1 2),
12.某几何体的一条棱长为 7 ,在该几何体的正视图中,这条棱的投影是长为 6 的线段,在该几何体
的侧视图与俯视图中,这条棱的投影分别是长为 a和 b 的线段,则 a+b 的最大值为( )
A. 2 2 B. 2 3 C.4 D. 2 5
第Ⅱ卷
本卷包括必考题和选考题两部分.第 13 题~第 21 题为必考题,每个试题考生都必须做答.第 22 题~
第 24 题为选考题,考生根据要求做答.
二、填空题:本大题共 4 小题,每小题 5 分.
13.已知向量 (0 11) , ,a , (4 1 0) ,,b , 29 a b 且 0 ,则 .
14.设双曲线
2 2
1
9 16
x y
的右顶点为 A,右焦点为 F.过点 F 平行双曲线的一条渐近线的直线与双曲线交
于点 B,则△AFB 的面积为 .
15.一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱
柱的体积为
9
8
,底面周长为 3,则这个球的体积为 .
16.从甲、乙两品种的棉花中各抽测了 25 根棉花的纤维长度(单位:mm),结果如下:
甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307
308 310 314 319 323 325 325 328 331 334 337 352
乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318
320 322 322 324 327 329 331 333 336 337 343 356
由以上数据设计了如下茎叶图
3 1 27
7 5 5 0 28 4
5 4 2 29 2 5
8 7 3 3 1 30 4 6 7
9 4 0 31 2 3 5 5 6 8
8
8 5 5 3 32 0 2 2 4 7 9
7 4 1 33 1 3 6 7
34 3
2 35 6
甲 乙
根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:
① ;
② .
三、解答题:解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分 12 分)
已知 na 是一个等差数列,且 2 1a , 5 5a .
(Ⅰ)求 na 的通项 na ;
(Ⅱ)求 na 前 n项和 Sn的最大值.
18.(本小题满分 12 分)
如图,已知点 P 在正方体 ABCD A B C D 的对角线 BD上, 60PDA .
(Ⅰ)求 DP 与CC所成角的大小;
(Ⅱ)求 DP 与平面 AA D D 所成角的大小.
A B
CD
PA B
CD
19.(本小题满分 12 分)
A B, 两个投资项目的利润率分别为随机变量 X1和 X2.根据市场分析,X1和 X2的分布列分别为
X1 5% 10%
P
0.8 0.2
(Ⅰ)在 A B, 两个项目上各投资 100 万元,Y1 和 Y2分别表示投资项目
A 和 B 所获得的利润,求方差 DY1,DY2;
(Ⅱ)将 (0 100)x x≤ ≤ 万元投资 A 项目, 100 x 万元投资 B 项
目, ( )f x 表示投资 A 项目所得利润的方差与投资 B 项目所得利润的方差的和.求 ( )f x 的最小值,并指出
x 为何值时, ( )f x 取到最小值.
(注:
2( )D aX b a DX )
20.(本小题满分 12 分)
在直角坐标系 xOy 中,椭圆 C1: 2
2
2
2
b
y
a
x
=1(a>b>0)的左、右焦点分别为 F1,F2.F2也是抛物线 C2:
2 4y x
的焦点,点 M 为 C1与 C2在第一象限的交点,且|MF2|=
3
5
.
(Ⅰ)求 C1的方程;
(Ⅱ)平面上的点 N 满足 21 MFMFMN ,直线 l∥MN,且与 C1交于 A,B 两点,若 0OA OB
,求
直线 l 的方程.
21.(本小题满分 12 分)
设函数
1( ) ( )f x ax a b
x b
Z, ,曲线 ( )y f x 在点 (2 (2))f, 处的切线方程为 y=3.
(Ⅰ)求 ( )f x 的解析式:
X2 2% 8% 12%
P
0.2 0.5 0.3
(Ⅱ)证明:函数 ( )y f x 的图像是一个中心对称图形,并求其对称中心;
(Ⅲ)证明:曲线 ( )y f x 上任一点的切线与直线 x=1 和直线 y=x 所围三角形的面积为定值,并求出此定
值.
请考生在第 22、23、24 题中任选一题做答,如果多做,则按所做的第一题记分.做答时,用 2B 铅笔在答
题卡上把所选题目对应的题号涂黑.
22.(本小题满分 10 分)选修 4-1:几何证明选讲
如图,过圆O外一点M 作它的一条切线,切点为 A,过 A点作直线 AP垂直直线OM ,垂足为 P.
(Ⅰ)证明:
2OM OP OA ;
(Ⅱ)N 为线段 AP上一点,直线 NB垂直直线ON,且交圆O于 B点.过 B点的切线交直线ON于K.证
明: 90OKM ∠ .
23.(本小题满分 10 分)选修 4-4;坐标系与参数方程
已知曲线 C1:
cos
sin
x
y
,
( 为参数),曲线 C2:
2 2
2
2
2
x t
y
,
(t 为参数).
(Ⅰ)指出 C1,C2各是什么曲线,并说明 C1与 C2公共点的个数;
(Ⅱ)若把 C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线 1 2C C , .写出 1 2C C , 的参数方
程. 1C 与 2C 公共点的个数和 C 21 C与 公共点的个数是否相同?说明你的理由.
24.(本小题满分 10 分)选修 4-5:不等式选讲
已知函数 ( ) 8 4f x x x .
(Ⅰ)作出函数 ( )y f x 的图像;
(Ⅱ)解不等式 8 4 2x x .
1
1
O x
y
O M
A
P
N
B
K
2009 年高考理科数学试题及答案-海南卷(同宁夏卷)
2009 年普通高等学校招生全国统一考试(宁夏卷)
数学(理工农医类)
一、选择题(每小题 5 分,共 60 分)
(1)已知集合 M={x|-3
0,V=S-T
(B) A<0,V=S-T
(C) A>0, V=S+T
(D)A<0, V=S+T
【解析】月总收入为 S,因此 A>0 时归入 S,判断框内填 A>0
支出 T 为负数,因此月盈利 V=S+T
【答案】C
(11)正六棱锥 P-ABCDEF 中,G 为 PB 的中点,则三棱锥 D-GAC
与三棱锥 P-GAC 体积之比为
(A)1:1 (B) 1:2 (C) 2:1 (D) 3:2
【解析】由于 G 是 PB 的中点,故 P-GAC 的体积等于 B-GAC 的体积
在底面正六边形 ABCDER 中
BH=ABtan30°= 3
3
AB
而 BD= 3 AB
故 DH=2BH
于是 VD-GAC=2VB-GAC=2VP-GAC
【答案】C
(12)若 1x 满足 2x+ 2x =5, 2x 满足 2x+2 2log (x-1)=5, 1x + 2x =
(A)
5
2
(B)3 (C)
7
2
(D)4
A B
C
DE
F
H
【解析】由题意
1
12 2 5xx ①
2 2 22 2log ( 1) 5x x ②
所以
1
12 5 2x x , 1 2 1log (5 2 )x x
即 2 1 2 12log (5 2 )x x
令 2x1=7-2t,代入上式得 7-2t=2log2(2t-2)=2+2log2(t-1)
∴5-2t=2log2(t-1)与②式比较得 t=x2
于是 2x1=7-2x2
【答案】C
(13)某企业有 3 个分厂生产同一种电子产品,第一、二、三分厂的产量之比为 1:2:1,用分层抽样方
法(每个分厂的产品为一层)从 3 个分厂生产的电子产品中共取 100 件作使用寿命的测试,由所得
的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为 980h,1020h,1032h,
则抽取的 100 件产品的使用寿命的平均值为 h.
【解析】
980 1+1020 2+1032 1
4
x
=1013
【答案】1013
(14)等差数列 na 的前 n项和为 nS ,且 5 36 5 5,S S 则 4a
【解析】∵Sn=na1+
1
2
n(n-1)d
∴S5=5a1+10d,S3=3a1+3d
∴6S5-5S3=30a1+60d-(15a1+15d)=15a1+45d=15(a1+3d)=15a4
【答案】 3
1
(15)设某几何体的三视图如下(尺寸的长度单位为 m)。
则该几何体的体积为
3m
【解析】这是一个三棱锥,高为 2,底面三角形一边为 4,这边上的高为 3,
体积等于
1
6
×2×4×3=4
【答案】4
(16)以知 F 是双曲线
2 2
1
4 12
x y
的左焦点, (1, 4),A P是双曲线右支上的动点,则 PF PA 的最小值
为 。
【解析】注意到 P 点在双曲线的两只之间,且双曲线右焦点为 F’(4,0),
于是由双曲线性质|PF|-|PF’|=2a=4
而|PA|+|PF’|≥|AF’|=5
两式相加得|PF|+|PA|≥9,当且仅当 A、P、F’三点共线时等号成立.
【答案】9
(17)(本小题满分 12 分)
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D 为两岛上的两座灯塔的塔顶。测量船于水面 A 处
测得 B 点和 D 点的仰角分别为
075 ,
030 ,于水面 C 处测得 B 点和 D 点的仰角均为
060 ,AC=0.1km。试探
究图中 B,D 间距离与另外哪两点间距离相等,然后求 B,D的距离(计算结果精确到 0.01km, 2 1.414,
6 2.449)
(17)解:
在△ABC 中,∠DAC=30°, ∠ADC=60°-∠DAC=30,
所以 CD=AC=0.1 又∠BCD=180°-60°-60°=60°,
故 CB 是△CAD 底边 AD 的中垂线,所以 BD=BA, ……5 分
在△ABC 中, ,
ABCsin
C
BCAsin
AAB
即 AB= ,
20
623
15sin
ACsin60
因此,BD= 。km33.0
20
623
故 B,D的距离约为 0.33km。 ……12 分
(18)(本小题满分 12 分)
如图,已知两个正方行 ABCD 和 DCEF 不在同一平面内,M,N 分别为 AB,DF 的中点。
(I)若平面 ABCD ⊥平面 DCEF,求直线 MN 与平面 DCEF 所成角的正值弦;
(II)用反证法证明:直线 ME 与 BN 是两条异面直线。
(18)(I)解法一:
取 CD 的中点 G,连接 MG,NG。
设正方形 ABCD,DCEF 的边长为 2,
则 MG⊥CD,MG=2,NG= 2 .
因为平面 ABCD⊥平面 DCED,
所以 MG⊥平面 DCEF,
可得∠MNG 是 MN 与平面 DCEF 所成的角。因为 MN= 6 ,所以 sin∠MNG=
3
6 为 MN 与平面 DCEF 所成角的
正弦值 ……6 分
解法二:
设正方形 ABCD,DCEF 的边长为 2,以 D 为坐标原点,分别以射线 DC,DF,DA 为 x,y,z 轴正半轴建立空
间直角坐标系如图.
则 M(1,0,2),N(0,1,0),可得MN
=(-1,1,2).
又DA
=(0,0,2)为平面 DCEF 的法向量,
可得
6cos( , )
3| || |
MN DAMN DA
MN DA
所以 MN 与平面 DCEF 所成角的正弦值为
cos 3
6
, DAMN · ……6 分
(Ⅱ)假设直线 ME 与 BN 共面, ……8 分
则 AB平面 MBEN,且平面 MBEN 与平面 DCEF 交于 EN
由已知,两正方形不共面,故 AB平面 DCEF。
又 AB//CD,所以 AB//平面 DCEF。面 EN 为平面 MBEN 与平面 DCEF 的交线,
所以 AB//EN。
又 AB//CD//EF,
所以 EN//EF,这与 EN∩EF=E 矛盾,故假设不成立。
所以 ME 与 BN 不共面,它们是异面直线. ……12 分
(19)(本小题满分 12 分)
某人向一目射击 4 次,每次击中目标的概率为。该目标分为 3 个不同的部分,第一、二、三部分面积
之比为 1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
(Ⅰ)设 X 表示目标被击中的次数,求 X 的分布列;
(Ⅱ)若目标被击中 2 次,A 表示事件“第一部分至少被击中 1 次或第二部分被击中 2 次”,求 P(A)
(19)解:
(Ⅰ)依题意 X 的分列为
0 1 2 3 4
P 16
81
32
81
24
81
8
81
1
81
………………6 分
(Ⅱ)设 A1表示事件“第一次击中目标时,击中第 i 部分”,i=1,2.
B1表示事件“第二次击中目标时,击中第 i 部分”,i=1,2.
依题意知 P(A1)=P(B1)=0.1,P(A2)=P(B2)=0.3,
1
3
1 1 1 1 1 1 2 2A A B A B A B A B ,
所求的概率为
1 1 1 1 1 1 2 2( ) ( ) ( ) ( )P A P A B P A B P A B P A B ( )
1 1 1 1 1 1 2 2( ) ( ) ( ) ) ( ) ( ) ( )P A B P A P B P A P B P A P B (
0.1 0.9 0.9 0.1 0.1 0.1 0.3 0.3 0.28 ………12 分
(20)(本小题满分 12 分)
已知,椭圆 C 过点 A
3(1, )
2
,两个焦点为(-1,0),(1,0)。
(1) 求椭圆 C 的方程;
(2) E,F 是椭圆 C 上的两个动点,如果直线 AE 的斜率与 AF 的斜率互为相反数,证明直线 EF 的斜率为
定值,并求出这个定值。
(20)解:
(Ⅰ)由题意,c=1,可设椭圆方程为 2 2
1 9 1
1 4b b
,解得
2 3b ,
2 3
4
b (舍去)
所以椭圆方程为
2 2
1
4 3
x y
。 ……………4 分
(Ⅱ)设直线 AE 方程为:
3( 1)
2
y k x ,代入
2 2
1
4 3
x y
得
2 2 23(3 4 ) 4 (3 2 ) 4( ) 12 0
2
k x k k x k
设 (x , y )E EE , (x , y )F FF ,因为点
3(1, )
2
A 在椭圆上,所以
2
2
34( ) 12
2x
3 4F
k
k
3
2E Ey kx k ………8 分
又直线 AF 的斜率与 AE 的斜率互为相反数,在上式中以—K 代 K,可得
2
2
34( ) 12
2x
3 4F
k
k
3
2E Ey kx k
所以直线 EF 的斜率
( ) 2 1
2
F E F E
EF
F E F E
y y k x x k
K
x x x x
即直线 EF 的斜率为定值,其值为
1
2
。 ……12 分
(21)(本小题满分 12 分)
已知函数 f(x)=
2
1
x 2
-ax+(a-1) ln x, 1a 。
(1)讨论函数 ( )f x 的单调性;
(2)证明:若 5a ,则对任意 x 1,x 2 (0, ) ,x 1 x 2 ,有 1 2
1 2
( ) ( ) 1f x f x
x x
。
(21)解:(1) ( )f x 的定义域为 (0, ) 。
2
' 1 1 ( 1)( 1 )( ) a x ax a x x af x x a
x x x
2 分
(i)若 1 1a 即 2a ,则
2
' ( 1)( ) xf x
x
故 ( )f x 在 (0, ) 单调增加。
(ii)若 1 1a ,而 1a ,故1 2a ,则当 ( 1,1)x a 时,
' ( ) 0f x ;
当 (0, 1)x a 及 (1, )x 时,
' ( ) 0f x
故 ( )f x 在 ( 1,1)a 单调减少,在 (0, 1), (1, )a 单调增加。
(iii)若 1 1a ,即 2a ,同理可得 ( )f x 在 (1, 1)a 单调减少,在 (0,1), ( 1, )a 单调增加.
(II)考虑函数 ( ) ( )g x f x x
21 ( 1) ln
2
x ax a x x
则
21 1( ) ( 1) 2 ( 1) 1 ( 1 1)a ag x x a x a a
x x
g
由于 1b>0)的左、右焦点,过 1F 斜率为 1 的直线l 与 E 相较于 A,B 两点,
且 2AF , AB , 2BF 成等差数列.
(Ⅰ)求 E 的离心率;
(Ⅱ)设点 P(0,-1)满足 PA PB ,求 E 的方程.
(21)(本小题满分 12 分)
设函数 f(x)=
21xe x ax .
(Ⅰ)若 a=0,求 f(x)的单调区间;
(Ⅱ)若当 x≥0 时 f(x)≥0,求 a 的取值范围.
[来源:Z*xx*k.Com]
[来源:Zxxk.Com]
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.答时用 2B 铅笔
在答题卡上把所选题目的题号涂黑.
(22) (本小题满分 10 分) 选修 4—1;几何证明选讲
如图,已知圆上的弧AC =BD ,过 C 点的圆的切线与 BA 的延长线交于 E 点,证明:
(Ⅰ) ACE = BCD ;
(Ⅱ)
2BC BE CD ;
(23) (本小题满分 10 分)选修 4—4;坐标系与参数方程
已知直线 1C :
1 cos .
sin ,
x t
y t
(t 为参数),圆 2C :
cos ,
sin ,
x
y
( 为参数),
(Ⅰ)当 =
3
时,求 1C 与 2C 的交点坐标;
(Ⅱ)过坐标原点 O作 1C 的垂线,垂足为 A,P 为 OA 的中点,当 变化时,求 P 点轨迹的参数方程,
并指出它是什么曲线;
[来源:Z§xx§k.Com]
(24) (24) (本小题满分 10 分)选修 4—5;不等式选讲
设函数 f(x)= 2 4 1x
(Ⅰ)画出函数 y=f(x)的图像;
(Ⅱ)若不等式 f(x)≤ax 的解集非空,求 a 的取值范围.
2011 年普通高等学校招生全国统一考试
理科数学
第 I卷
一、选择题:本大题共 12 小题,每小题 5分,在每小题给出的四个选项中,只有一项是符合
题目要求的。
(1)复数
2
1 2
i
i
的共轭复数是
(A)
3
5
i (B)
3
5
i (C) i (D) i
(2)下列函数中,既是偶函数又在 +(0, )单调递增的函数是
(A) 3y x (B) 1y x (C) 2 1y x (D) 2 xy
(3)执行右面的程序框图,如果输入的 N是 6,那么输出的 p是
(A)120
(B)720
(C)1440
(D)5040
(4)有 3 个兴趣小组,甲、乙两位同学各自参加其中一个 小组,每
位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为
(A)
1
3
(B)
1
2
(C)
2
3
(D)
3
4
(5)已知角 的顶点与原点重合,始边与 x轴的正半轴重合,终边在直线 2y x 上,则 cos 2 =
(A)
4
5
(B)
3
5
(C)
3
5
(D)
4
5
(6)在一个几何体的三视图中,正视图和俯视图如右图所示,
则相应的俯视图可以为
(7)设直线 L过双曲线 C的一个焦点,且与 C的一条对称轴垂直,L与 C交于 A ,B 两点,AB
为 C的实轴长的 2倍,则 C的离心率为
(A) 2 (B) 3 (C)2 (D)3
(8)
512ax x
x x
的展开式中各项系数的和为 2,则该展开式中常数项为
(A)-40 (B)-20 (C)20 (D)40
(9)由曲线 y x ,直线 2y x 及 y轴所围成的图形的面积为
(A)
10
3
(B)4 (C)
16
3
(D)6
(10)已知 a与 b均为单位向量,其夹角为,有下列四个命题
1
2: 1 0,
3
P a b
2
2: 1 ,
3
P a b
3 : 1 0,
3
P a b
4 : 1 ,
3
P a b
其中的真命题是
(A) 1 4,P P (B) 1 3,P P (C) 2 3,P P (D) 2 4,P P
( 11 ) 设 函 数 ( ) sin( ) cos( )( 0, )
2
f x x x 的 最 小 正 周 期 为 , 且
( ) ( )f x f x ,则
(A) ( )f x 在 0,
2
单调递减 (B) ( )f x 在
3,
4 4
单调递减
(C) ( )f x 在 0,
2
单调递增 (D) ( )f x 在
3,
4 4
单调递增
(12)函数
1
1
y
x
的图像与函数 2sin ( 2 4)y x x 的图像所有交点的横坐标之和等于
(A)2 (B) 4 (C) 6 (D)8
第Ⅱ卷
本卷包括必考题和选考题两部分。第 13 题~第 21 题为必考题,每个试题考生都必须做
答。第 22 题~第 24 题为选考题,考生根据要求做答。
二、填空题:本大题共 4小题,每小题 5分。
(13)若变量 ,x y满足约束条件
3 2 9,
6 9,
x y
x y
则 2z x y 的最小值为 。
(14)在平面直角坐标系 xOy中,椭圆C的中心为原点,焦点 1 2,F F 在 x轴上,离心率为
2
2
。
过 1F 的直线 L交 C于 ,A B两点,且 2ABFV 的周长为 16,那么C的方程为 。
(15)已知矩形 ABCD的顶点都在半径为 4 的球O的球面上,且 6, 2 3AB BC ,则棱锥
O ABCD 的体积为 。
(16)在 ABCV 中, 60 , 3B AC ,则 2AB BC 的最大值为 。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分 12 分)
等比数列 na 的各项均为正数,且
2
1 2 3 2 62 3 1, 9 .a a a a a
(Ⅰ)求数列 na 的通项公式;
(Ⅱ)设 3 1 3 2 3log log ...... log ,n nb a a a 求数列
1
nb
的前 n项和.
(18)(本小题满分 12 分)
如图,四棱锥 P-ABCD 中,底面 ABCD 为平行四
边形,∠DAB=60°,AB=2AD,PD⊥底面 ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若 PD=AD,求二面角 A-PB-C 的余弦值。
(19)(本小题满分 12 分)
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于 102
的产品为优质品,现用两种新配方(分别称为 A配方和 B 配方)做试验,各生产了 100 件这种产品,并测
量了每件产品的质量指标值,得到下面试验结果:
(Ⅰ)分别估计用 A 配方,B 配方生产的产品的优质品率;
(Ⅱ)已知用 B 配方生成的一件产品的利润 y(单位:元)与其质量指标值 t 的关系式为
从用 B 配方生产的产品中任取一件,其利润记为 X(单位:元),求 X 的分布列及数学期望.(以试验
结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
(20)(本小题满分 12 分)
在平面直角坐标系 xOy 中,已知点 A(0,-1),B 点在直线 y = -3 上,M 点满足 / /MB OA
uuur uur
,
MA AB MB BA
uuur uuur uuur uur
,M 点的轨迹为曲线 C。
(Ⅰ)求 C 的方程;
(Ⅱ)P 为 C 上的动点,l 为 C 在 P 点处得切线,求 O 点到 l距离的最小值。
(21)(本小题满分 12 分)
已知函数
ln( )
1
a x bf x
x x
,曲线 ( )y f x 在点 (1, (1))f 处的切线方程为 2 3 0x y 。
(Ⅰ)求 a、b的值;
(Ⅱ)如果当 0x ,且 1x 时,
ln( )
1
x kf x
x x
,求 k的取值范围。
请考生在第 22、23、24 题中任选一题做答,如果多做,则按所做的第一题记分。做答时请写清题号。
(22)(本小题满分 10 分)选修 4-1:几何证明选讲
如图,D, E分别为 ABC 的边 AB, AC上的点,且 不
与 ABC 的顶点重合。已知 AE的长为 n, AD, AB的长是 关
于 x的方程
2 14 0x x mn 的两个根。
(Ⅰ)证明:C, B,D,E四点共圆;
(Ⅱ)若 90A ,且 4, 6m n ,求C, B,D, E所在圆的半径。
(23)(本小题满分 10 分)选修 4-4:坐标系与参数方程
在直角坐标系 xOy 中,曲线 C1的参数方程为
2cos
2 2sin
x
y
( 为参数)
M 是 C1上的动点,P 点满足 2OP OM
uuuv uuuv
,P 点的轨迹为曲线 C2
(Ⅰ)求 C2的方程
(Ⅱ)在以 O 为极点,x 轴的正半轴为极轴的极坐标系中,射线
3
与 C1的异于极点的交点为 A,
与 C2的异于极点的交点为 B,求 AB .
(24)(本小题满分 10 分)选修 4-5:不等式选讲
设函数 ( ) 3f x x a x ,其中 0a 。
(Ⅰ)当 1a 时,求不等式 ( ) 3 2f x x 的解集;
(Ⅱ)若不等式 ( ) 0f x 的解集为 | 1x x ,求 a 的值。
参考答案
一、选择题
(1)C (2)B (3)B (4)A (5)B (6)D
(7)B (8)D (9)C (10)A (11)A (12)D
二、填空题
(13)-6 (14)
2 2
1
16 8
x y
(15)8 3 (16) 2 7
三、解答题
(17)解:
(Ⅰ)设数列{an}的公比为 q,由
2
3 2 69a a a 得
3 2
3 49a a 所以
2 1
9
q 。
由条件可知 a>0,故
1
3
q 。
由 1 22 3 1a a 得 1 22 3 1a a q ,所以 1
1
3
a 。
故数列{an}的通项式为 an=
1
3n
。
(Ⅱ ) 3 1 3 2 3 nlog log ... lognb a a a
(1 2 ... )
( 1)
2
n
n n
故
1 2 1 12( )
( 1) 1nb n n n n
1 2
1 1 1 1 1 1 1 1 2... 2((1 ) ( ) ... ( ))
2 2 3 1 1n
n
b b b n n n
所以数列
1{ }
nb
的前 n 项和为
2
1
n
n
(18)解:
(Ⅰ)因为 60 , 2DAB AB AD , 由余弦定理得 3BD AD
从而 BD2+AD2= AB2,故 BD AD
又 PD底面 ABCD,可得 BD PD
所以 BD平面 PAD. 故 PA BD
(Ⅱ)如图,以 D 为坐标原点,AD 的长为单位长,射线 DA 为 x轴的正半轴建立空间直角坐标系 D- xyz,
则
1,0,0A , 0 3,0B , , 1, 3,0C , 0,0,1P 。
( 1, 3,0), (0, 3, 1), ( 1,0,0)AB PB BC
uuuv uuv uuuv
设平面 PAB 的法向量为 n=(x,y,z),则
0,
0,
{n AB
n PB
uuur
uuur
即
3 0
3 0
x y
y z
因此可取 n= ( 3,1, 3)
设平面 PBC 的法向量为 m,则
m 0,
m 0,
{ PB
BC
uuur
uuur
可取 m=(0,-1, 3 )
4 2 7cos ,
72 7
m n
故二面角 A-PB-C 的余弦值为
2 7
7
(19)解
(Ⅰ)由试验结果知,用 A 配方生产的产品中优质的平率为
22 8 =0.3
100
,所以用 A 配方生产的产品
的优质品率的估计值为 0.3。
由试验结果知,用 B 配方生产的产品中优质品的频率为
32 10 0.42
100
,所以用 B配方生产的产品的
优质品率的估计值为 0.42
(Ⅱ)用 B 配方生产的 100 件产品中,其质量指标值落入区间 90,94 , 94,102 , 102,110 的频率分
别为 0.04,,054,0.42,因此
P(X=-2)=0.04, P(X=2)=0.54, P(X=4)=0.42,
即 X 的分布列为
X 的数学期望值 EX=-2×0.04+2×0.54+4×0.42=2.68
(20)解:
(Ⅰ)设 M(x,y),由已知得 B(x,-3),A(0,-1).
所以MA
uuur
=(-x,-1-y), MB
uuur
=(0,-3-y), AB
uuur
=(x,-2).
再由题意可知(MA
uuur
+MB
uuur
)• AB
uuur
=0, 即(-x,-4-2y)• (x,-2)=0.
所以曲线 C 的方程式为 y=
1
4
x
2
-2.
(Ⅱ)设 P(x 0 ,y 0 )为曲线 C:y=
1
4
x
2
-2 上一点,因为 y
'
=
1
2
x,所以 l的斜率为
1
2
x 0
因此直线 l的方程为 0 0 0
1 ( )
2
y y x x x ,即
2
0 0 02 2 0x x y y x 。
则 O 点到 l的距离
2
0 0
2
0
| 2 |
4
y xd
x
.又
2
0 0
1 2
4
y x ,所以
2
0
2
02 2
0 0
1 4 1 42 ( 4 ) 2,
24 4
x
d x
x x
当
2
0x =0 时取等号,所以 O点到 l距离的最小值为 2.
(21)解:
(Ⅰ) 2 2
1( ln )
'( )
( 1)
x x bxf x
x x
由于直线 2 3 0x y 的斜率为
1
2
,且过点 (1,1) ,故
(1) 1,
1'(1) ,
2
f
f
即
1,
1 ,
2 2
b
a b
解得 1a , 1b 。
(Ⅱ)由(Ⅰ)知
ln 1f ( )
1
xx
x x
,所以
2
2
ln 1 ( 1)( 1)( ) ( ) (2 ln )
1 1
x k k xf x x
x x x x
。
考虑函数 ( ) 2 lnh x x
2( 1)( 1)k x
x
( 0)x ,则
2
2
( 1)( 1) 2'( ) k x xh x
x
。
(i)设 0k ,由
2 2
2
( 1) ( 1)'( ) k x xh x
x
知,当 1x 时, '( ) 0h x 。而 (1) 0h ,故
当 (0,1)x 时, ( ) 0h x ,可得 2
1 ( ) 0
1
h x
x
;
当 x(1,+)时,h(x)<0,可得 21
1
x
h(x)>0
从而当 x>0,且 x 1 时,f(x)-(
1
ln
x
x
+
x
k
)>0,即 f(x)>
1
ln
x
x
+
x
k
.
(ii)设 00,故
'h (x)>0,而
h(1)=0,故当 x(1,
k1
1
)时,h(x)>0,可得 21
1
x
h(x)<0,与题设矛盾。
(iii)设 k 1.此时
'h(x)>0,而 h(1)=0,故当 x(1,+)时,h(x)>0,可得 21
1
x
h(x)
<0,与题设矛盾。
综合得,k 的取值范围为(-,0]
(22)解:
(I)连接 DE,根据题意在△ADE 和△ACB 中,
AD×AB=mn=AE×AC,
即
AB
AE
AC
AD
.又∠DAE=∠CAB,从而△ADE∽△ACB
因此∠ADE=∠ACB
所以 C,B,D,E 四点共圆。
(Ⅱ)m=4, n=6 时,方程 x
2
-14x+mn=0 的两根为 x1=2,x2=12.
故 AD=2,AB=12.
取 CE 的中点 G,DB 的中点 F,分别过 G,F 作 AC,AB 的垂线,两垂线相交于 H 点,连接 DH.因为 C,B,
D,E四点共圆,所以 C,B,D,E 四点所在圆的圆心为 H,半径为 DH.
由于∠A=90
0
,故 GH∥AB, HF∥AC. HF=AG=5,DF=
2
1
(12-2)=5.
故 C,B,D,E 四点所在圆的半径为 5 2
(23)解:
(I)设 P(x,y),则由条件知 M(
2
,
2
YX
).由于 M 点在 C1上,所以
sin22
2
,cos2
2
y
x
即
sin44
cos4
y
x
从而 2C 的参数方程为
4cos
4 4sin
x
y
( 为参数)
(Ⅱ)曲线 1C 的极坐标方程为 4sin ,曲线 2C 的极坐标方程为 8sin 。
射线
3
与 1C 的交点 A的极径为 1 4sin
3
,
射线
3
与 2C 的交点 B的极径为 2 8sin
3
。
所以 2 1| | | | 2 3AB .
(24)解:
(Ⅰ)当 1a 时, ( ) 3 2f x x 可化为
| 1| 2x 。
由此可得 3x 或 1x 。
故不等式 ( ) 3 2f x x 的解集为
{ | 3x x 或 1}x 。
( Ⅱ) 由 ( ) 0f x 得
3 0x a x
此不等式化为不等式组
3 0
x a
x a x
或
3 0
x a
a x x
即
4
x a
ax
或
2
x a
aa
因为 0a ,所以不等式组的解集为 |
2
ax x
由题设可得
2
a
= 1 ,故 2a
2012 年普通高等学校招生全国统一考试
理科数学
注息事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考证号
填写在本试卷和答题卡相应位置上。
2.问答第Ⅰ卷时。选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动.用橡皮
擦干净后,再选涂其它答案标号。写在本试卷上无效.
3.回答第Ⅱ卷时。将答案写在答题卡上.写在本试卷上无效·
4.考试结束后.将本试卷和答且卡一并交回。
第一卷
一. 选择题:本大题共 12 小题,每小题 5 分,在每小题给同的四个选项中,只有一项是符合题目要
求的。
(1)已知集合 {1, 2,3, 4,5}A , {( , ) , , }B x y x A y A x y A ;,则 B中所含元素的个数为( )
( )A 3 ( )B 6 ( )C ( )D
【解析】选D
5, 1, 2,3, 4x y , 4, 1, 2,3x y , 3, 1, 2x y , 2, 1x y 共 10 个
(2)将 2名教师, 4名学生分成2 个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教
师和 2名学
生组成,不同的安排方案共有( )
( )A 12种 ( )B 10种 ( )C 种 ( )D 种
【解析】选 A 甲地由1名教师和 2名学生: 1 2
2 4 12C C 种
(3)下面是关于复数
2
1
z
i
的四个命题:其中的真命题为( )
1 : 2p z 2
2 : 2p z i 3 :p z的共轭复数为1 i 4 :p z的虚部为 1
( )A 2 3,p p ( )B 1 2,p p ( )C ,p p ( )D ,p p
【解析】选C
2 2( 1 ) 1
1 ( 1 )( 1 )
iz i
i i i
1 : 2p z , 2
2 : 2p z i , 3 :p z的共轭复数为 1 i , 4 :p z的虚部为 1
(4)设 1 2F F 是椭圆
2 2
2 2: 1( 0)x yE a b
a b
的左、右焦点,P为直线
3
2
ax 上一点, 2 1F PF 是底角
为30的
等腰三角形,则E的离心率为( )
( )A 1
2
( )B 2
3
( )C
( )D
【解析】选C
2 1F PF 是 底 角 为 30 的 等 腰 三 角 形
2 2 1
3 32( ) 2
2 4
cPF F F a c c e
a
(5)已知 na 为等比数列, 4 7 2a a , 5 6 8a a ,则 1 10a a ( )
( )A 7 ( )B 5 ( )C ( )D
【解析】选D
4 7 2a a , 5 6 4 7 4 78 4, 2a a a a a a 或 4 72, 4a a
4 7 1 10 1 104, 2 8, 1 7a a a a a a
4 7 10 1 1 102, 4 8, 1 7a a a a a a
(6)如果执行右边的程序框图,输入正整数 ( 2)N N 和
实数 1 2, ,..., na a a ,输出 ,A B,则( )
( )A A B 为 1 2, ,..., na a a 的和
( )B
2
A B
为 1 2, ,..., na a a 的算术平均数
( )C A和 B分别是 1 2, ,..., na a a 中最大的数和最小的数
( )D A和 B分别是 1 2, ,..., na a a 中最小的数和最大的数 【解析】选C
(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,
则此几何体的体积为( )
( )A 6 ( )B 9 ( )C ( )D
【解析】选 B 该几何体是三棱锥,底面是俯视图,高为3
此几何体的体积为
1 1 6 3 3 9
3 2
V
(8)等轴双曲线C的中心在原点,焦点在 x轴上,C与抛物线 xy 162
的准线交于 ,A B两点, 4 3AB ;则C的实轴长为( )
( )A 2 ( )B 2 2 ( )C ( )D
【解析】选 C 设
2 2 2: ( 0)C x y a a 交 xy 162 的准线 : 4l x 于
( 4, 2 3)A ( 4, 2 3)B 得: 2 2 2( 4) (2 3) 4 2 2 4a a a
(9)已知 0 ,函数 ( ) sin( )
4
f x x 在 ( , )
2
上单调递减。则的取值范围
是( )
( )A 1 5[ , ]
2 4
( )B 1 3[ , ]
2 4
( )C 1(0, ]
2
( )D (0, 2]
【解析】选 A 5 92 ( ) [ , ]
4 4 4
x 不合题意排除 ( )D ,
3 51 ( ) [ , ]
4 4 4
x 合题意
排除 ( )( )B C
另: ( ) 2
2
,
3( ) [ , ] [ , ]
4 2 4 4 2 2
x
得:
3 1 5,
2 4 2 4 2 2 4
(10) 已知函数
1( )
ln( 1)
f x
x x
;则 ( )y f x 的图像大致为( )
【解析】选 B
( ) ln(1 ) ( )
1
( ) 0 1 0, ( ) 0 0 ( ) (0) 0
xg x x x g x
x
g x x g x x g x g
得: 0x 或 1 0x 均有 ( ) 0f x 排除 , ,A C D
(11)已知三棱锥 S ABC 的所有顶点都在球O的求面上, ABC 是边长为1的正三角形,
SC为球O的直径,且 2SC ;则此棱锥的体积为( )
( )A 2
6
( )B 3
6
( )C 2
3
( )D 2
2
【解析】选 A
ABC 的外接圆的半径
3
3
r ,点O到面 ABC的距离 2 2 6
3
d R r
SC为球O的直径点 S到面 ABC的距离为
2 62
3
d
此棱锥的体积为
1 1 3 2 6 22
3 3 4 3 6ABCV S d
另:
1 32
3 6ABCV S R 排除 , ,B C D
(12)设点 P在曲线
1
2
xy e 上,点Q在曲线 ln(2 )y x 上,则 PQ 最小值为( )
( )A 1 ln 2 ( )B 2(1 ln 2) ( )C 1 ln 2 ( )D 2(1 ln 2)
【解析】选 A
函数
1
2
xy e 与函数 ln(2 )y x 互为反函数,图象关于 y x 对称
函数
1
2
xy e 上的点
1( , )
2
xP x e 到直线 y x 的距离为
1
2
2
xe x
d
设函数 min min
1 1 1 ln 2( ) ( ) 1 ( ) 1 ln 2
2 2 2
x xg x e x g x e g x d
由图象关于 y x 对称得: PQ 最小值为 min2 2(1 ln 2)d
第Ⅱ卷
本卷包括必考题和选考题两部分。第 13 题~第 21 题为必考题,每个试题考生都必须作答,第 22-第 24 题
为选考题,考生根据要求做答。
二.填空题:本大题共 4 小题,每小题 5 分。
(13)已知向量 ,a b
夹角为45
,且 1, 2 10a a b
;则 _____b
【解析】 _____b
3 2
222 10 (2 ) 10 4 4 cos 45 10 3 2a b a b b b b
(14) 设 ,x y满足约束条件:
, 0
1
3
x y
x y
x y
;则 2z x y 的取值范围为
【解析】 2z x y 的取值范围为 [ 3,3]
约束条件对应四边形OABC边际及内的区域: (0,0), (0,1), (1, 2), (3,0)O A B C
则 2 [ 3,3]z x y
(15)某个部件由三个元件按下图方式连接而成,元件 1 或元件 2 正常工作,且元件 3 正常工作,则部件
正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布
2(1000,50 )N ,且各个元件能否正
常相互独立,那么该部件的使用寿命超过 1000 小时的概率为
【解析】使用寿命超过 1000 小时的概率为
3
8
三个电子元件的使用寿命均服从正态分布
2(1000,50 )N
得:三个电子元件的使用寿命超过 1000 小时的概率为
1
2
p
超过 1000 小时时元件 1 或元件 2 正常工作的概率 2
1
31 (1 )
4
P p
那么该部件的使用寿命超过 1000 小时的概率为 2 1
3
8
p p p
(16)数列{ }na 满足 1 ( 1) 2 1n
n na a n ,则{ }na 的前60 项和为
【解析】{ }na 的前60项和为 1830新课 标 第 一网
可证明: 1 4 1 4 2 4 3 4 4 4 3 4 2 4 2 4 16 16n n n n n n n n n nb a a a a a a a a b
1 1 2 3 4 15
15 1410 10 15 16 1830
2
b a a a a S
三、解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分 12 分)
已知 , ,a b c分别为 ABC 三个内角 , ,A B C的对边, cos 3 sin 0a C a C b c
(1)求 A ; (2)若 2a , ABC 的面积为 3 ;求 ,b c。
【解析】(1)由正弦定理得:
cos 3 sin 0 sin cos 3 sin sin sin sina C a C b c A C A C B C
sin cos 3 sin sin sin( ) sin
13 sin cos 1 sin( 30 )
2
30 30 60
A C A C a C C
A A A
A A
(2)
1 sin 3 4
2
S bc A bc
2 2 2 2 cos 4a b c bc A b c
解得: 2b c
18.(本小题满分 12 分)
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不
完,剩下的玫瑰花作垃圾处理。
(1)若花店一天购进16枝玫瑰花,求当天的利润 y (单位:元)关于当天需求量 n(单位:枝, n N )
的函数解析式。
(2)花店记录了 100 天玫瑰花的日需求量(单位:枝),整理得下表:
以 100 天记录的各需求量的频率作为各需求量发生的概率。
(i)若花店一天购进16枝玫瑰花, X 表示当天的利润(单位:元),求 X 的分布列,数学期望及方
差;
(ii)若花店计划一天购进 16 枝或 17 枝玫瑰花,你认为应购进 16 枝还是 17 枝?请说明理由。
【解析】(1)当 16n 时, 16 (10 5) 80y
当 15n 时, 5 5(16 ) 10 80y n n n 得:
10 80( 15)
( )
80 ( 16)
n n
y n N
n
(2)(i) X 可取60 ,70 ,80 ( 60) 0.1, ( 70) 0.2, ( 80) 0.7P X P X P X
X 的 分布列为
60 0.1 70 0.2 80 0.7 76EX
2 2 216 0.1 6 0.2 4 0.7 44DX
(ii)购进 17 枝时,当天的利润为
(14 5 3 5) 0.1 (15 5 2 5) 0.2 (16 5 1 5) 0.16 17 5 0.54 76.4y
76.4 76 得:应购进 17 枝
(19)(本小题满分 12 分)
如图,直三棱柱 1 1 1ABC ABC 中, 1
1
2
AC BC AA ,
D是棱 1AA 的中点, BDDC 1
(1)证明: BCDC 1
(2)求二面角 11 CBDA 的大小。
【解析】(1)在 Rt DAC 中, AD AC
得: 45ADC
同理: 1 1 145 90ADC CDC
得: 1 1 1,DC DC DC BD DC 面 1BCD DC BC
(2) 1 1,DC BC CC BC BC 面 1 1ACC A BC AC
取 1 1A B 的中点O,过点O作OH BD 于点H ,连接 1 1,CO C H
1 1 1 1 1 1 1AC BC CO AB ,面 1 1 1A BC 面 1ABD 1CO 面 1ABD
1OH BD C H BD 得:点H 与点D重合
且 1C DO 是二面角 11 CBDA 的平面角
X 60 70 80
P 0.1 0.2 0.7
设 AC a ,则 1
2
2
aC O , 1 1 12 2 30C D a CO C DO
既二面角 11 CBDA 的大小为30
(20)(本小题满分 12 分)
设抛物线
2: 2 ( 0)C x py p 的焦点为 F ,准线为 l, A C ,已知以 F 为圆心,
FA为半径的圆 F 交 l于 ,B D两点;
(1)若 090BFD , ABD 的面积为 24 ;求 p的值及圆 F 的方程;
(2)若 , ,A B F三点在同一直线m上,直线 n与m平行,且 n与C只有一个公共点,
求坐标原点到 ,m n距离的比值。
【解析】(1)由对称性知: BFD 是等腰直角,斜边 2BD p
点 A到准线 l的距离 2d FA FB p
14 2 4 2 2
2ABDS BD d p
圆 F 的方程为
2 2( 1) 8x y
(2)由对称性设
2
0
0 0( , )( 0)
2
xA x x
p
,则 (0, )
2
pF
点 ,A B关于点 F 对称得:
2 2
2 20 0
0 0( , ) 3
2 2 2
x x pB x p p x p
p p
得:
3( 3 , )
2
pA p ,直线
3
32 2: 3 0
2 23
p p
p pm y x x y
p
2
2 3 32
2 3 3
x xx py y y x p
p p
切点
3( , )
3 6
p pP
直线
3 3 3: ( ) 3 0
6 3 3 6
p pn y x x y p
坐标原点到 ,m n距离的比值为
3 3: 3
2 6
p p
。
(21)(本小题满分 12 分)
已知函数 ( )f x 满足满足 1 21( ) (1) (0)
2
xf x f e f x x ;
(1)求 ( )f x 的解析式及单调区间;
(2)若 21( )
2
f x x ax b ,求 ( 1)a b 的最大值。
【解析】(1) 1 2 11( ) (1) (0) ( ) (1) (0)
2
x xf x f e f x x f x f e f x
令 1x 得: (0) 1f
1 2 11( ) (1) (0) (1) 1 (1)
2
xf x f e x x f f e f e
得: 21( ) ( ) ( ) 1
2
x xf x e x x g x f x e x
( ) 1 0 ( )xg x e y g x 在 x R 上单调递增
( ) 0 (0) 0, ( ) 0 (0) 0f x f x f x f x
得: ( )f x 的解析式为 21( )
2
xf x e x x
且单调递增区间为 (0, ) ,单调递减区间为 ( ,0)
(2) 21( ) ( ) ( 1) 0
2
xf x x ax b h x e a x b 得 ( ) ( 1)xh x e a
①当 1 0a 时, ( ) 0 ( )h x y h x 在 x R 上单调递增
x时, ( )h x 与 ( ) 0h x 矛盾
②当 1 0a 时, ( ) 0 ln( 1), ( ) 0 ln( 1)h x x a h x x a
得:当 ln( 1)x a 时, min( ) ( 1) ( 1) ln( 1) 0h x a a a b
2 2( 1) ( 1) ( 1) ln( 1)( 1 0)a b a a a a
令
2 2( ) ln ( 0)F x x x x x ;则 ( ) (1 2 ln )F x x x
( ) 0 0 , ( ) 0F x x e F x x e
当 x e 时, max( )
2
eF x
当 1,a e b e 时, ( 1)a b 的最大值为
2
e
请考生在第 22,23,24 题中任选一题做答,如果多做,则按所做的第一题计分,
做答时请写清题号。
(22)(本小题满分 10 分)选修 4-1:几何证明选讲
如图, ,D E分别为 ABC 边 ,AB AC的中点,直线DE交
ABC 的外接圆于 ,F G两点,若 / /CF AB,证明:
(1)CD BC ;
(2) BCD GBD
【解析】(1) / /CF AB, / / / / / /DF BC CF BD AD CD BF
/ /CF AB AF BC BC CD
(2) / /BC GF BG FC BD
/ /BC GF GDE BGD DBC BDC BCD GBD
(23)本小题满分 10 分)选修 4—4;坐标系与参数方程
已知曲线 1C 的参数方程是 )(
3siny
2cosx
为参数
,以坐标原点为极点, x轴的正半轴
为极轴建立坐标系,曲线 2C 的坐标系方程是 2 ,正方形 ABCD的顶点都在 2C 上,
且 , , ,A B C D依逆时针次序排列,点 A的极坐标为 (2, )
3
(1)求点 , , ,A B C D的直角坐标;
(2)设 P为 1C 上任意一点,求
2 2 2 2PA PB PC PD 的取值范围。
【解析】(1)点 , , ,A B C D的极坐标为
5 4 11(2, ), (2, ), (2, ), (2, )
3 6 3 6
点 , , ,A B C D的直角坐标为 (1, 3), ( 3,1), ( 1, 3), ( 3, 1)
(2)设 0 0( , )P x y ;则
0
0
2cos
( )
3sin
x
y
为参数
2 2 2 2 2 24 4 40t PA PB PC PD x y
256 20sin [56,76]
(24)(本小题满分 10 分)选修 4 5 :不等式选讲
已知函数 ( ) 2f x x a x
(1)当 3a 时,求不等式 ( ) 3f x 的解集;
(2)若 ( ) 4f x x 的解集包含[1,2],求 a的取值范围。
【解析】(1)当 3a 时, ( ) 3 3 2 3f x x x
2
3 2 3
x
x x
或
2 3
3 2 3
x
x x
或
3
3 2 3
x
x x
1x 或 4x
(2)原命题 ( ) 4f x x 在[1,2]上恒成立
2 4x a x x 在[1,2]上恒成立
2 2x a x 在[1,2]上恒成立
3 0a
2013 年普通高等学校招生全国统一考试
理 科 数 学
(新课标 I 卷)使用省份:河北、河南、山西、陕西
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第 II 卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考
证号填写在本试卷和答题卡相应位置上。
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡
皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第 I卷
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一个是符合题目要求的.
(1)已知集合 022 xxxA , 55B xx ,则
(A) BA ∅ (B) RBA (C) AB (D) BA
(2)若复数 z满足 i34i43 z
(A) 4 (B)
5
4
(C)4 (D)
5
4
(3)为了解某地区中小学生的视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已经了
解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大.在
下面的抽样方法中,最合理的抽样方法是
(A)简单的随机抽样 (B)按性别分层抽样
(C)按学段分层抽样 (D)系统抽样
(4)已知双曲线C: )0,0(12
2
2
2
ba
b
y
a
x
的离心率为
2
5
,则C的渐近线方程为
(A) xy
4
1
(B) xy
3
1
(C) xy
2
1
(D) xy
(5)执行右面的程序框图,如果输入的 31t , ,则输出的 s属于
(A) 43,
(B) 25,
(C) 34,
(D) 52,
(6)如图,有一个水平放置的透明无盖的正方体容器,容器 高 8 cm,
将一个球放在容器口,再向容器注水,当球面恰好接触水面时 测得水深为
6 cm,如不计容器的厚度,则球的体积为
(A) 3cm
3
500π
(B) 3cm
3
866π
(C) 3cm
3
1372π
(D) 3cm
3
2048π
(7)设等差数列 na 的前 n项和为 nS ,若 21 mS , 0mS , 31 mS ,则 m
(A)3 (B)4 (C)5 (D)6
(8)某几何体的三视图如图所示,则该几何体的体积为
(A) 8π16
(B) 8π8
(C) π6116
(D) 16π8
(9)设m为正整数, myx 2 展开式的二项式系数的最大值为 a, 12 myx 展开式的二项式系数的最
大值为b,若 ba 713 ,则m=
(A)5 (B)6 (C)7 (D)8
(10)已知椭圆E: )0(12
2
2
2
ba
b
y
a
x
的右焦点为 )03( ,F ,过点F 的直线交椭圆 E于 A、B两点。
若 AB的中点坐标为 )11( , ,则 E的方程为
(A) 1
3645
22
yx
(B) 1
2736
22
yx
(C) 1
1827
22
yx
(D) 1
918
22
yx
(11)已知函数
0),1(ln
02
)(
2
>xx
x,x
xf ,若 axxf )( ,则 a的取值范围是
(A) 0, (B) 1, (C) 12, (D) 02,
A
P
B
C
(12)设 nnn CBA △ 的三边长分别为 na , nb , nc , nnn CBA △ 的面积为 nS , 3,2,1n ……
若 1b > 1c , 111 2acb , nn aa 1 ,
2
n
1
acb n
n
,
2
n
1
abc n
n
,则
(A) nS 为递减数列
(B) nS 为递增数列
(C) 12 nS 为递增数列, nS2 为递减数列
(D) 12 nS 为递减数列, nS2 为递增数列
第Ⅱ卷
本卷包括必考题和选考题两部分。第 13 题~第 21 题为必考题,每个试题考生都必须作答。第 22 题~
第 24 题为选考题,考生依据要求作答。
二.填空题:本大题共 4 小题,每小题 5 分.
(13)已知两个单位向量a ,b 的夹角为 60°, bac )1( tt .若 cb =0,则
t =____________.
(14)若数列 na 的前 n项和为
3
1
3
2
n naS ,则数列 na 的通项公式是 na =____________.
(15)设当 θx 时,函数 xxxf cos2sin)( 取得最大值,则 cos =____________.
(16)若函数 ))(1()( 22 baxxxxf 的图像关于直线 2x 对称,则 )(xf 的最大值
为____________.
三、解答题:解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分 12 分)
如图,在 ABC△ 中, ABC =90°, 3AB , 1BC ,
A
C 1C
1B
1A
B
P为 ABC△ 内一点, BPC =90°
(Ⅰ)若
2
1
PB ,求 PA;
(Ⅱ)若 APB =150°,求 PBAtan .
(18)(本小题满分 12 分)
如图,三棱柱 111 CBAABC 中, CBCA , 1AAAB , 1BAA =60°.
(Ⅰ)证明 AB⊥ CA1 ;
(Ⅱ)若平面 ABC⊥平面 BBAA 11 , CBAB ,求直 线 CA1
与平面 CCBB 11 所成角的正弦值。
(19)(本小题满分 12 分)
一批产品需要进行质量检验,检验方案是:先从这批产品中任取 4 件作检验,这 4 件产品中优质品的
件数记为 n .如果 3n ,再从这批产品中任取 4件作检验,若都为优质品,则这批产品通过检验;如果 4n ,
再从这批产品中任取 1 件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过
检验.
假设这批产品的优质品率为 50%,即取出的产品是优质品的概率都为
2
1
,且各件产品是否为优质品相
互独立.
(Ⅰ)求这批产品通过检验的概率;
(Ⅱ)已知每件产品检验费用为 100 元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需
的费用记为 X (单位:元),求 X 的分布列及数学期望。
(20)(本小题满分 12 分)
已知圆M : 1)1( 22 yx ,圆 N : 9)1( 22 yx ,动圆 P与圆M 外切并与圆 N 内切,圆心P
的轨迹为曲线C .
(Ⅰ)求C的方程;
(Ⅱ) l是与圆P,圆M 都相切的一条直线, l与曲线C交于 A, B两点,当圆 P的半径最长时,
D
C
B
E
A
求 AB .
(21)(本小题满分 12 分)
已知函数 baxxxf 2)( , )()( dcxexg x 若曲线 )(xfy 和曲线 )(xgy 都过点 )2,0(P ,
且在点 P处有相同的切线 24 xy .
(Ⅰ)求 a,b, c, d 的值;
(Ⅱ)若 x -2 时, )()( xkgxf ,求 k的取值范围.
请考生在第 22、23、24 题中任选一道作答,并用 2B 铅笔将答题卡上所选的题目对应的题号右侧方框涂黑,
按所涂题号进行评分;多涂、多答,按所涂的首题进行评分,不涂,按本选考题的首题进行评分.
(22)(本小题满分 10 分)选修 4—1:几何证明选讲
如图,直线 AB为圆的切线,切点为 B,点C在圆上,
∠ ABC的角平分线 BE交圆于点 E,DB垂直 BE交圆于 D .
(Ⅰ)证明: DCDB ;
(Ⅱ)设圆的半径为 1, 3BC ,延长CE交 AB于 点 F ,
求 BCF△ 外接圆的半径.
(23)(本小题满分 10 分)选修 4—4:坐标系与参数方程
已知曲线 1C 的参数方程式
ty
tx
sin55
cos54
( t为参数),以坐标原点为极点,以坐标原点为极点,x轴
的正半轴为极轴建立极坐标系,曲线 2C 的极坐标方程为 sin2 .
(Ⅰ)把 1C 的参数方程化为极坐标方程;
(Ⅱ)求 1C 与 2C 交点的极坐标( 0 , π20 )
(24)(本小题满分 10 分)选修 4—5:不等式选讲
已知函数 axxxf 212)( , 3)( xxg .
(Ⅰ)当 2a 时,求不等式 )()( xgxf 的解集;
(Ⅱ)设 1a ,且当 )
2
1,
2
[ ax 时, )()( xgxf ,求 a的取值范围.