2020版高考数学二轮复习 专题六 统计 专题突破练18 统计与统计案例 文

2020版高考数学二轮复习 专题六 统计 专题突破练18 统计与统计案例 文

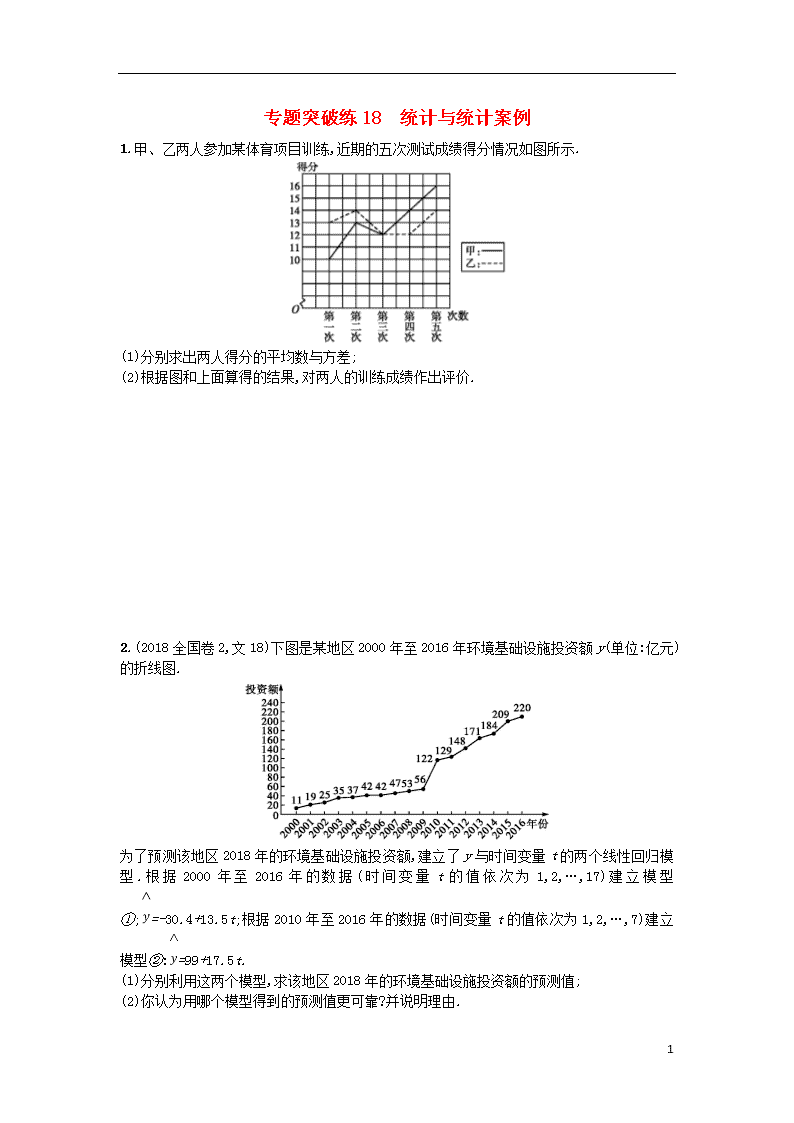
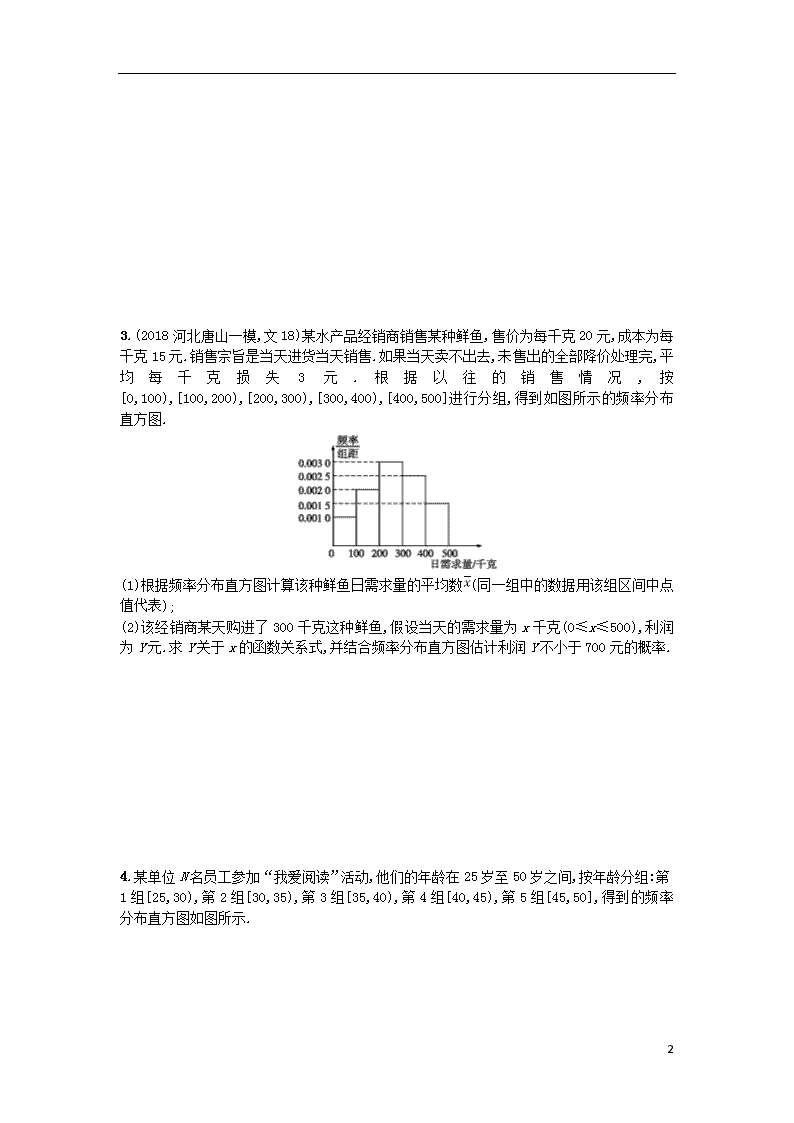
专题突破练18　统计与统计案例 ‎1.甲、乙两人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.‎ ‎(1)分别求出两人得分的平均数与方差;‎ ‎(2)根据图和上面算得的结果,对两人的训练成绩作出评价.‎ ‎2.(2018全国卷2,文18)下图是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图.‎ 为了预测该地区2018年的环境基础设施投资额,建立了y与时间变量t的两个线性回归模型.根据2000年至2016年的数据(时间变量t的值依次为1,2,…,17)建立模型①;=-30.4+13.5t;根据2010年至2016年的数据(时间变量t的值依次为1,2,…,7)建立模型②:=99+17.5t.‎ ‎(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;‎ ‎(2)你认为用哪个模型得到的预测值更可靠?并说明理由.‎ 11‎ ‎3.(2018河北唐山一模,文18)某水产品经销商销售某种鲜鱼,售价为每千克20元,成本为每千克15元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价处理完,平均每千克损失3元.根据以往的销售情况,按[0,100),[100,200),[200,300),[300,400),[400,500]进行分组,得到如图所示的频率分布直方图.‎ ‎(1)根据频率分布直方图计算该种鲜鱼日需求量的平均数(同一组中的数据用该组区间中点值代表);‎ ‎(2)该经销商某天购进了300千克这种鲜鱼,假设当天的需求量为x千克(0≤x≤500),利润为Y元.求Y关于x的函数关系式,并结合频率分布直方图估计利润Y不小于700元的概率.‎ ‎4.某单位N名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.‎ 11‎ ‎(1)求正整数a,b,N的值;‎ ‎(2)现要从年龄低于40岁的员工中用分层抽样的方法抽取42人,则年龄在第1,2,3组的员工人数分别抽取多少?‎ ‎(3)为了估计该单位员工的阅读倾向,现对该单位所有员工中按性别比例抽查的40人是否喜欢阅读国学类书籍进行了调查,调查结果如下所示:(单位:人)‎ 喜欢阅读国学类 不喜欢阅读国学类 合计 男 ‎14‎ ‎4‎ ‎18‎ 女 ‎8‎ ‎14‎ ‎22‎ 合计 ‎22‎ ‎18‎ ‎40‎ 下面是年龄的分布表:‎ 区间 ‎[25,30)‎ ‎[30,35)‎ ‎[35,40)‎ ‎[40,45)‎ ‎[45,50]‎ 人数 ‎28‎ a b 根据表中数据,我们能否有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?‎ 附:K2=,其中n=a+b+c+d.‎ P(K2≥k0)‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎5.(2018百校联盟四月联考,文18)每年的寒冷天气都会带热“御寒经济”,以餐饮业为例,当外面太冷时,不少人都会选择叫外卖上门,外卖商家的订单就会增加,下表是某餐饮店从外卖数据中抽取的5天的日平均气温与外卖订单数.‎ 日平均气温(℃)‎ ‎-2‎ ‎-4‎ ‎-6‎ ‎-8‎ ‎-10‎ 外卖订单数(份)‎ ‎50‎ ‎85‎ ‎115‎ ‎140‎ ‎160‎ 11‎ ‎(1)经过数据分析,一天内平均气温x(℃)与该店外卖订单数y(份)成线性相关关系,试建立y关于x的回归方程,并预测气温为‎-12 ℃‎时该店的外卖订单数(结果四舍五入保留整数);‎ ‎(2)天气预报预测未来一周内(七天),有3天日平均气温不高于‎-10 ℃‎,若把这7天的预测数据当成真实数据,则从这7天任意选取2天,求恰有1天外卖订单数不低于160份的概率.‎ 附注:回归方程x+中斜率和截距的最小二乘估计公式分别为:.‎ ‎6.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:‎ 旧养殖法 11‎ 新养殖法 ‎(1)记A表示事件“旧养殖法的箱产量低于‎50 kg”,估计A的概率;‎ ‎(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关;‎ 箱产量<‎‎50 kg 箱产量≥‎‎50 kg 旧养殖法 新养殖法 ‎(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.‎ 附:,‎ K2‎‎=.‎ ‎7.‎ 11‎ 某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.‎ 分数段 ‎[40,50)‎ ‎[50,60)‎ ‎[60,70)‎ ‎[70,80)‎ ‎[80,90)‎ ‎[90,100]‎ 男 ‎3‎ ‎9‎ ‎18‎ ‎15‎ ‎6‎ ‎9‎ 女 ‎6‎ ‎4‎ ‎5‎ ‎10‎ ‎13‎ ‎2‎ ‎(1)估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;‎ ‎(2)规定80分以上为优分(含80分),请你根据已知条件作出2×2列联表,并判断是否在犯错误的概率不超过0.1的前提下认为“数学成绩与性别有关”.‎ 优　分 非优分 合　计 男生 女生 合计 ‎100‎ 附表及公式 P(K2≥k0)‎ ‎0.100‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k0‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ K2=,其中n=a+b+c+d.‎ ‎8.(2018全国百强校最后一卷,文19)下表为2014年至2017年某百货零售企业的线下销售额(单位:万元),其中年份代码x=年份-2 013.‎ 年份代码x ‎1‎ ‎2‎ ‎3‎ ‎4‎ 线下销售额y ‎95‎ ‎165‎ ‎230‎ ‎310‎ ‎(1)已知y与x具有线性相关关系,求y关于x的线性回归方程,并预测2018年该百货零售企业的线下销售额;‎ 11‎ ‎(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调査平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了55位男顾客、50位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有10人、女顾客有20人,能否在犯错误的概率不超过0.025的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?‎ 参考公式及数据:‎ ‎,‎ K2‎‎=,n=a+b+c+d.‎ P(K2≥k0)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ 参考答案 专题突破练18　统计与统计案例 ‎1.解 (1)由图象可得甲、乙两人五次测试的成绩分别为 甲:10分,13分,12分,14分,16分;乙:13分,14分,12分,12分,14分.‎ ‎=13,‎ ‎=13,‎ 11‎ ‎×[(10-13)2+(13-13)2+(12-13)2+(14-13)2+(16-13)2]=4,‎ ‎×[(13-13)2+(14-13)2+(12-13)2+(12-13)2+(14-13)2]=0.8.‎ ‎(2)由,可知乙的成绩较稳定.‎ 从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的成绩在不断提高,而乙的成绩则无明显提高.‎ ‎2.解 (1)利用模型①,该地区2018年的环境基础设施投资额的预测值为=-30.4+13.5×19=226.1(亿元).‎ 利用模型②,该地区2018年的环境基础设施投资额的预测值为=99+17.5×9=256.5(亿元).‎ ‎(2)利用模型②得到的预测值更可靠.‎ 理由如下:‎ ‎(i)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y=-30.4+13.5t上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型=99+17.5t可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.‎ ‎(ii)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.‎ ‎(以上给出了2种理由,答出其中任意一种或其他合理理由均可得分)‎ ‎3.解 (1)=50×0.001 0×100+150×0.002 0×100+250×0.003 0×100+350×0.002 5×100+450×0.001 5×100=265.‎ ‎(2)当日需求量不低于300千克时,利润Y=(20-15)×300=1 500(元);当日需求量不足300千克时,利润Y=(20-15)x-(300-x)×3=8x-900(元);‎ 故Y=‎ 由Y≥700得,200≤x≤500,‎ 所以P(Y≥700)=P(200≤x≤500)=0.003 0×100+0.002 5×100+0.001 5×100=0.7.‎ 11‎ ‎4.解 (1)总人数N==280,a=28,第3组的频率是1-5×(0.02+0.02+0.06+0.02)=0.4,‎ 所以b=280×0.4=112.‎ ‎(2)因为年龄低于40岁的员工在第1,2,3组,共有28+28+112=168(人),‎ 利用分层抽样在168人中抽取42人,每组抽取的人数分别为:‎ 第1组抽取的人数为28×=7(人),‎ 第2组抽取的人数为28×=7(人),‎ 第3组抽取的人数为112×=28(人),‎ 所以第1,2,3组分别抽7人、7人、28人.‎ ‎(3)假设H0:“是否喜欢阅读国学类书籍和性别无关”,根据表中数据,‎ 求得K2的观测值 k=≈6.860 5>6.635,‎ 查表得P(K2≥6.635)=0.01,从而能有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系.‎ ‎5.解 (1)由题意可知=-6,‎ ‎=110,‎ ‎(xi-)2=42+22+02+(-2)2+(-4)2=40,‎ ‎(xi-)(yi-)=4×(-60)+2×(-25)+0×5+(-2)×30+(-4)×50=-550,‎ 所以=-13.75,=110+13.75×(-6)=27.5,‎ 11‎ 所以y关于x的回归方程为=-13.75x+27.5,‎ 当x=-12时,=-13.75x+27.5=-13.75×(-12)+27.5=192.5≈193.‎ 所以可预测当平均气温为‎-12 ℃‎时,该店的外卖订单数为193份.‎ ‎(2)外卖订单数不低于160份的概率就是日平均气温不高于‎-10 ℃‎的概率,‎ 由题意,设日平均气温不高于‎-10 ℃‎的3天分别记作A,B,C,另外4天记作a,b,c,d,‎ 从这7天中任取2天结果有:(A,B),(A,C),(A,a),(A,b),(A,c),(A,d),(B,C),(B,a),(B,b),(B,c),(B,d),(C,a),(C,b),(C,c),(C,d),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)共21种,‎ 恰有1天平均气温不高于‎-10 ℃‎的结果有:‎ ‎(A,a),(A,b),(A,c),(A,d),(B,a),(B,b),(B,c),(B,d),(C,a),(C,b),(C,c),(C,d)共12种,‎ 所以所求概率P=.‎ ‎6.解 (1)旧养殖法的箱产量低于‎50 kg的频率为 ‎(0.012+0.014+0.024+0.034+0.040)×5=0.62.‎ 因此,事件A的概率估计值为0.62.‎ ‎(2)根据箱产量的频率分布直方图得列联表 箱产量<‎‎50 kg 箱产量≥‎‎50 kg 旧养殖法 ‎62‎ ‎38‎ 新养殖法 ‎34‎ ‎66‎ K2‎‎=≈15.705.‎ 由于15.705>6.635,故有99%的把握认为箱产量与养殖方法有关.‎ ‎(3)箱产量的频率分布直方图表明:新养殖法的箱产量平均值(或中位数)在‎50 kg到‎55 kg之间,旧养殖法的箱产量平均值(或中位数)在‎45 kg到‎50 kg之间,且新养殖法的箱产量分布集中程度较旧养殖法的箱产量分布集中程度高,因此,可以认为新养殖法的箱产量较高且稳定,从而新养殖法优于旧养殖法.‎ ‎7.解 (1)=45×0.05+55×0.15+65×0.3+75×0.25+85×0.1+95×0.15=71.5.‎ ‎=45×0.15+55×0.10+65×0.125+75×0.25+85×0.325+95×0.05=71.5.‎ 从男、女生各自的成绩平均分来看,并不能判断数学成绩与性别有关.‎ ‎(2)由频数分布表可知,在抽取的100名学生中,“男生组”中的优分有15人,“女生组”中的优分有15人,据此可得2×2列联表如下:‎ 优　分 非优分 合　计 男生 ‎15‎ ‎45‎ ‎60‎ 11‎ 女生 ‎15‎ ‎25‎ ‎40‎ 合计 ‎30‎ ‎70‎ ‎100‎ 可得K2=≈1.79.‎ ‎∵1.79<2.706,∴在犯错误的概率不超过0.1的前提下不能认为“数学成绩与性别有关”.‎ ‎8.解 (1)由题意得=2.5,=200,=30,xiyi=2 355,所以=71,‎ 所以=200-71×2.5=22.5,‎ 所以y关于x的线性回归方程为=71x+22.5.‎ 由于2 018-2 013=5,所以当x=5时,=71×5+22.5=377.5,‎ 所以预测2018年该百货零售企业的线下销售额为377.5万元.‎ ‎(2)由题可得2×2列联表如下:‎ 持乐观态度 持不乐观态度 总计 男顾客 ‎10‎ ‎45‎ ‎55‎ 女顾客 ‎20‎ ‎30‎ ‎50‎ 总计 ‎30‎ ‎75‎ ‎105‎ 故K2的观测值 K2‎‎=≈6.109,‎ 由于6.109>5.024,所以可以在犯错误的概率不超过0.025 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关.‎ 11‎