上海市2014高考数学压轴卷试题目文含解析

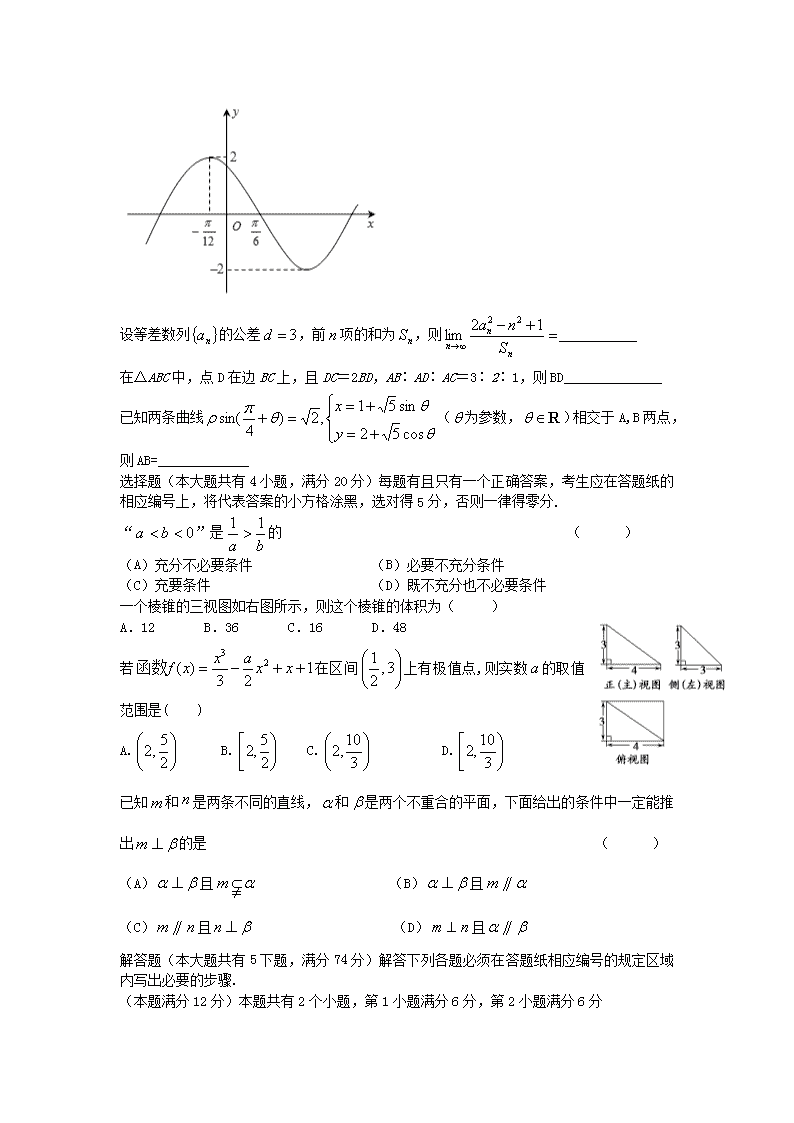
上海市2014高考数学压轴卷试题目文含解析

‎2014年上海高考数学押题卷（文）‎ 考生注意：‎ ‎1.答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号，并将核对后的条形码贴在指定位置上，在答题纸反面清楚地填写姓名.‎ ‎2.本试卷共有23道试题，满分150分.考试时间120分钟.‎ 填空题（本大题共有14题，满分56分）考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分.‎ 命题,使得，则为_____________‎ 的定义域为_____________‎ 已知是抛物线的焦点，直线与抛物线相交于两点，线段AB的中点，则直线的斜率是_____________‎ 已知是定义在上的奇函数.当时，，则不等式 在R上的解集是_____________‎ 已知数列其前项和为，且，则数列的通项公式为_____________‎ 零向量满足,则夹角是_____________‎ 已知直线和直线，抛物线上一动点 到直线和直线的距离之和的最小值是_____________‎ 已知实数满足，若取得最大值时的唯一最优解是，则实数=____________‎ 已知复数，则b=_____________‎ 已知_____________‎ 已知函数（其中，，)的部分图象如图所示。则函数f(x)的解析式是_____________‎ 设等差数列的公差，前项的和为，则 ‎ 在△ABC中，点D在边BC上，且DC＝2BD，AB∶AD∶AC＝3∶2∶1，则BD______________‎ 已知两条曲线（为参数，）相交于A,B两点，则AB=_____________‎ 选择题（本大题共有4小题，满分20分）每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分.‎ ‎“”是的 （ ）‎ ‎（A）充分不必要条件 （B）必要不充分条件 ‎（C）充要条件 （D）既不充分也不必要条件 一个棱锥的三视图如右图所示，则这个棱锥的体积为（ ）‎ A．12 B．36 C．16 D．48 ‎ 若在区间上有极值点,则实数的取值范围是( )‎ A. B. C. D.‎ 已知和是两条不同的直线，和是两个不重合的平面，下面给出的条件中一定能推出的是 （ ）‎ ‎（A）且 （B）且 ‎ ‎（C）且 （D）且 解答题（本大题共有5下题，满分74分）解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.‎ ‎（本题满分12分）本题共有2个小题，第1小题满分6分，第2小题满分6分 如图，平面ABB1A1为圆柱OO1的轴截面，点C为上的点， 点M为BC中点．‎ ‎（1）求证：B1M∥平面O1AC；‎ ‎（2）若2r = AB＝AA1，∠CAB=30°，求三棱锥A到平面O1BM的距离．‎ ‎（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.‎ A B D O C x y ‎(第16题图)‎ 在平面直角坐标系xOy中，角α的顶点是坐标原点，始边为x轴的正半轴，终边与单位圆O交于点A(x1 ，y1 )，α∈(，)．将角α终边绕原点按逆时针方向旋转，交单位圆于点B(x2，y2)．‎ ‎（1）若x1＝，求x2；‎ ‎△BOD的面积分别为S1，S2，且S1＝S2，求tanα的值．‎ ‎(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分.‎ 已知各项均为正数的等比数列的首项，为其前项和，若成等差数列．‎ ‎（1）求数列的通项公式；‎ ‎（2）设，，记数列的前项和为. 若对于任意的，恒成立，求实数的取值范围.‎ ‎（本题满分16分）本题共有6个小题，第1小题满分5分，第2小题满分5分，第1小题满分6分.‎ ‎（1）试判断函数的单调性； ‎ ‎（2）设，求在上的最大值；‎ ‎(3) 试证明：对任意，不等式都成立（其中是自然对数的底数）．‎ ‎（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第2小题满分8分.‎ 已知椭圆，直线恒过的定点为椭圆的一个焦点，且椭圆上的点到焦点的最大距离为3.直线为垂直于轴的动弦，且均在椭圆上，定点，直线与直线交于点．‎ 求椭圆的方程；‎ 求证：点恒在椭圆上；‎ 求面积的最大值．‎ ‎ ‎ ‎2014年全国普通高等学校招生统一考试 上海数学押题卷（理工类）参考答案 填空题 ‎1-5 ‎ ‎6-10 2 ‎ ‎11-14 ‎ 选择题 A 16. A 17. C 18. C 解答题 ‎ （1）证明省略. （2）．‎ ‎（1）－ . （2）2．‎ ‎（1） （2）‎ ‎ （1）在上单调递增，在上单调递减.‎ ‎（2）． （3） 证明省略.‎ ‎（1） （2）证明省略. （3） .‎ ‎============================= 详细解析见下 ‎ ‎【答案】‎ ‎ 【解析】。‎ ‎【答案】‎ ‎ 【解析】‎ ‎【答案】‎ ‎ 【解析】‎ ‎【答案】‎ ‎ 【解析】‎ ‎【答案】‎ ‎ 【解析】‎ ‎【答案】 ‎ ‎ 【解析】‎ ‎。‎ ‎【答案】 2‎ ‎ 【解析】‎ ‎【答案】‎ ‎ 【解析】‎ ‎【答案】‎ ‎ 【解析】‎ ‎【答案】‎ ‎ 【解析】‎ ‎【答案】‎ ‎ 【解析】‎ ‎【答案】‎ ‎ 【解析】‎ ‎【答案】‎ ‎ 【解析】‎ ‎【答案】‎ ‎ 【解析】‎ ‎。‎ ‎【答案】（A）‎ ‎ 【解析】‎ ‎【答案】（A）‎ ‎ 【解析】‎ ‎。‎ ‎【答案】（C）‎ ‎ 【解析】‎ ‎【答案】（C）‎ ‎ 【解析】‎ ‎【答案】（1）证明省略. （2）.‎ ‎ 【解析】‎ ‎（1）‎ ‎（2） 利用等体积法，求点P到平面O1BM的距离d。‎ ‎【答案】（1）－, （2）2.‎ ‎ 【解析】（1）‎ 解法一：‎ 因为x1＝，y1＞0，所以y1＝＝．‎ ‎ 所以sinα＝，cosα＝． ………………………3分 所以x2＝cos(α＋)＝cosαcos－sinαsin＝－． ………………………6分 ‎ 解法二：‎ 因为x1＝，y1＞0，所以y1＝＝．A(，)，则＝(，).………2分 ‎ ＝(x2，y2)， 因为·＝||||cos∠AOB，所以x2＋y2＝ ……4分 ‎ 又x22＋y22＝1，联立消去y2得50 x22－30x2－7＝0‎ ‎ 解得x2＝－或，又x2＜0，所以x2＝－． ………………………6分 ‎ 解法三：‎ 因为x1＝，y1＞0，所以y1＝＝．因此A(，)，所以tanα＝．………2分 ‎ 所以tan(α＋)＝＝－7，所以直线OB的方程为y＝－7x ……4分 ‎ 由得x＝±，又x2＜0，所以x2＝－． …………………6分 ‎（2）S1＝sinαcosα＝－sin2α． …………………………………………8分 因为α(，)，所以α＋(，)．‎ ‎ 所以S2＝－sin(α＋)cos(α＋)＝－sin(2α＋)＝－cos2α．…………10分 ‎ 因为S1＝S2，所以sin2α＝－cos2α，即tan2α＝－． ……………12分 所以＝－，解得tanα＝2或tanα＝－． ‎ 因为α(，)，所以tanα＝2．………14分 ‎【KS5U答案】（1） （2）‎ ‎ 【KS5U解析】‎ ‎（1）设的公比为.∵成等差数列，‎ ‎ 即，化简得，‎ ‎ 解得：或 由已知， ……………6分 ‎ （2）由得 ‎ ‎ ‎ …………9分 ‎ …………12分 ‎ ，当且仅当即时等号成立，‎ ‎ 实数的取值范围是 ………14分 ‎【KS5U答案] （1）在上单调递增，在上单调递减 ‎（2）（3）证明省略；‎ ‎ 【KS5U解析】‎ ‎（1）函数的定义域是．由已知．令，得．‎ 因为当时，；当时，．‎ 所以函数在上单调递增，在上单调递减．……………………………5分 ‎（2）由（1）可知当，即时，在上单调递增，所以．当时，在上单调递减，所以．‎ 当，即时，．‎ 综上所述，………………………………………………10分 由（1）知当时．所以在时恒有，即，当且仅当时等号成立．因此对任意恒有．因为，，所以，即．‎ 因此对任意，不等式．………………………………16分 ‎【KS5U答案] （1） （2）证明省略. （3）.‎ ‎ 【KS5U解析】‎ ‎（1）直线可化为 ‎ ， 由得，‎ ‎ ， ， 又， ，‎ ‎ 椭圆的方程为 ………………………………………………4分 ‎ （2）设直线的方程为，则可设，且 ‎ 直线的方程为，直线的方程为 ‎ 联立求得交点，代入椭圆方程得，‎ ‎ ，化简得：‎ ‎ 点恒在椭圆上.……………………………………………………………10分 ‎ ②直线过点，设其方程为，‎ ‎ 联立得，‎ ‎ ‎ ‎ ，‎ ‎ 令，则 ‎ 在上是增函数， 的最小值为10.‎ ‎ ………………………………………18分