高考文科数学模拟题合集一

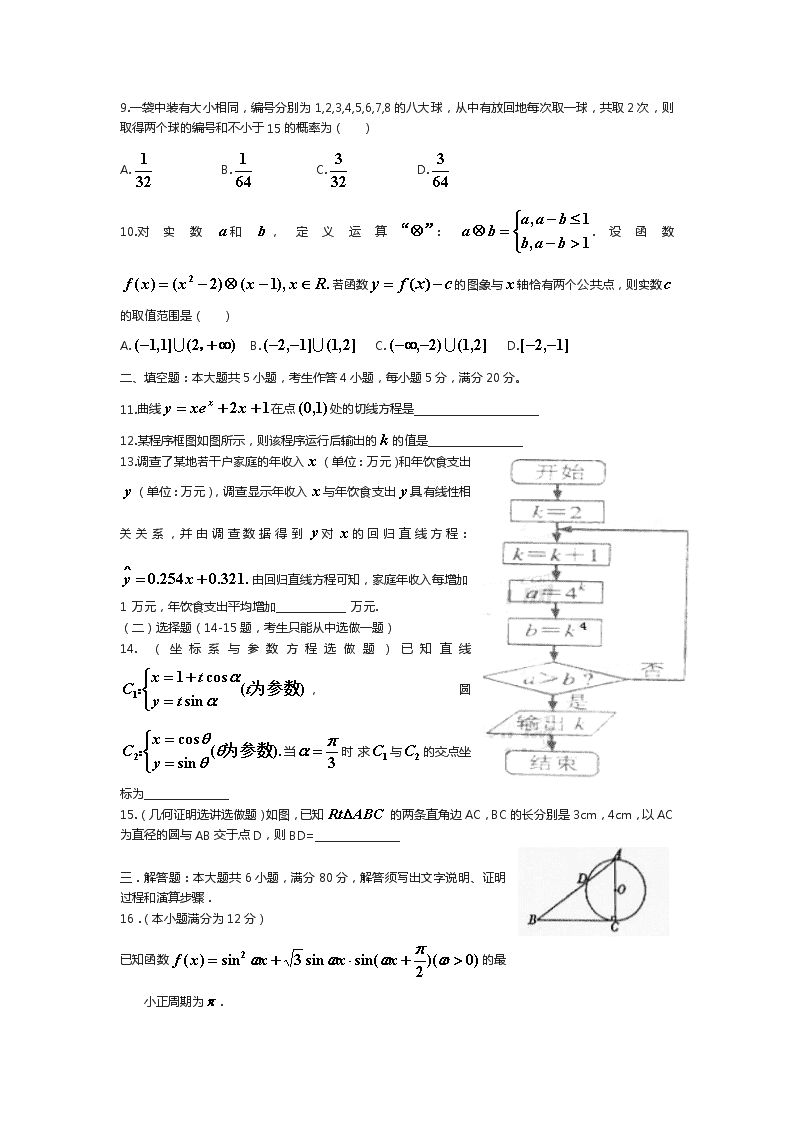
高考文科数学模拟题合集一

1. 设，则( )‎ A. ‎ B. C. D.‎ 2. 设集合，，则( )‎ A. ‎ B. C. D.‎ 3. 若非零向量满足，则与的夹角为（ ）‎ A. ‎ B. C. D.‎ 4. 若函数为奇函数，则（ ）‎ A. ‎ B. C. D.‎ 5. 设变量满足，则的最大值和最小值分别是（ ）‎ A.1，-1 B.2，‎-2 C.1，-2 D.2，-1‎ 6. 某几何体的三视图如图所示，则它的体积为（ ）‎ A. ‎ B. C. D.‎ 7. 设抛物线上一点P到轴的距离是4，则点P到该抛物线焦点的距离是（ ）‎ A.4 B‎.6 C.8 D.12‎ 8. 设是公差不为0等差数列，且成等比数列，则的前n项和=（ ）‎ A. ‎ B. C. D.‎ 9. 一袋中装有大小相同，编号分别为1,2,3,4,5,6,7,8的八大球，从中有放回地每次取一球，共取2次，则取得两个球的编号和不小于15的概率为（ ）‎ A. ‎ B. C. D.‎ 10. 对实数和，定义运算：.设函数若函数的图象与轴恰有两个公共点，则实数的取值范围是（ ）‎ A. B. C. D.‎ 二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分。‎ ‎11.曲线在点处的切线方程是_________________________‎ ‎12.某程序框图如图所示，则该程序运行后输出的的值是___________________‎ ‎13.调查了某地若干户家庭的年收入（单位：万元）和年饮食支出（单位：万元），调查显示年收入与年饮食支出具有线性相关关系，并由调查数据得到对的回归直线方程：由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加______________万元.‎ ‎（二）选择题（14-15题，考生只能从中选做一题）‎ ‎14.（坐标系与参数方程选做题）已知直线，圆当时，求与的交点坐标为_________________‎ ‎15.（几何证明选讲选做题）如图，已知的两条直角边AC，BC的长分别是‎3cm，‎4cm，以AC为直径的圆与AB交于点D，则BD=_________________‎ 三．解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程和演算步骤．‎ ‎16．（本小题满分为12分）‎ 已知函数的最小正周期为.‎ （1） 求的值；‎ （2） 求函数在区间上的取值范围.‎ 17． ‎（本小题满分12分）‎ 为了了解某工厂开展群众体育活动的情况，拟采用分层抽样的方法从A，B，C三个区中抽取7个工厂进行调查，已知A，B，C区中分别有18，27，18个工厂， （Ⅰ）求从A，B，C区中分别抽取的工厂个数； （Ⅱ）若从抽取的7个工厂中随机抽取2个进行调查结果的对比，用列举法计算这2个工厂中至少有1个来自A区的概率．‎ 18． ‎（本小题满分14分）‎ 如图，在四棱锥中，，,，,.‎ （1） 求证：；‎ （2） 求点到平面的距离.‎ ‎19．（本小题满分14分）‎ 设函数为奇函数，其图象在点处的切线与直线垂直，导函数的最小值为-12.‎ （1） 求的值；‎ （2） 求函数的单调递增区间，并求函数在上的最大值和最小值.‎ 20． ‎（本小题满分14分）‎ 已知数列满足 （1） 令，证明：是等比数列.‎ （2） 求的通项公式.‎ 21． ‎（本小题满分14分）‎ 如图，已知点，直线，为平面上的动点，过点作直线的垂线，垂足为点，且ｌ ‎－１１‎ Ｏ ‎１‎ ｘ ｙ Ｆ （1） 求动点的轨迹的方程；‎ （2） 过点的直线交轨迹于、两点，交直线于点.‎ ‎①已知求的值；‎ ‎②求的最小值.‎ 授益教育命题组——2015年高考模拟试题 数学试题（文科）‎ 注意事项：‎ ‎ 1．本试题分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试用时120分钟．‎ ‎ 2．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡及答题纸上．‎ ‎ 3．第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．答案不能答在试题卷上．‎ ‎ 4．第Ⅱ卷写在答题纸对应区域内，严禁在试题卷或草纸上答题．‎ ‎ 5．考试结束后，将答题卡和答题纸一并交回．‎ 第Ⅰ卷（选择题共60分）‎ 一、选择题（本大题共12小题。每小题5分，共60分．在每小题给出的四个选项中。只有一个符合题目要求的选项．）‎ ‎1．设P，Q为两个非空实数集合，定义集合，若 ‎，则P+Q中元素的个数为 （ ）‎ ‎ A．9 B．‎8 ‎C．7 D．6‎ ‎2．已知是实数，是虚数单位，则 （ ）‎ ‎ A． B． C． D．‎ ‎3．函数 （ ）‎ ‎ A．是奇函数，且在（-∞，+∞）上是减函数 ‎ ‎ B．是奇函数，且在（-∞，+∞）上是增函数 ‎ C．是偶函数，且在（-∞，+∞）上是减函数 ‎ ‎ D．是偶函数，且在（-∞，+∞）上是增函数 ‎4．已知各项不为0的等差数列，满足，数列是等比数列，且 （ ）‎ ‎ A．2 B．‎4 ‎C．8 D．16‎ ‎5．若是两条不同的直线，是三个不同的平面，给出下列命题：‎ ‎ ①若； ②若；‎ ‎ ③若； ④若 ‎ 其中正确命题的个数为 （ ）‎ ‎ A．1 B．‎2 ‎C．3 D．4‎ ‎6．圆心在直线上，经过原点，且在轴上截得弦长为2的圆的方程为（ ）‎ ‎ A．‎ ‎ B．‎ ‎ C．‎ ‎ D．‎ ‎7．如图是函数在区间上的图象，为了得到这个函数的图象，只要将的图象上所有的点 （ ）‎ ‎ A．向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变 ‎ B．向左平移个单位长度，再把所得各点的横坐标缩短到原来的2倍，纵坐标不变 ‎ C．向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变 ‎ D．向左平移个单位长度，再把所得各点的横坐标缩短到原来的2倍，纵坐标不变 ‎8．已知函数则函数零点的个数为（ ）‎ ‎ A．1 B．‎2 ‎C．3 D．4‎ ‎9．设双曲线的一个焦点为F，虚轴的一个端点为B，如果直线FB与该双曲线的一条渐近线垂直，那么此双曲线的离心率为 （ ）‎ ‎ A． B．‎ ‎ C． D．‎ ‎10．在中，内角A，B，C的对边分别是，若 （ ）‎ ‎ A． B．60‎ ‎ C．120 D．150‎ ‎11．函数若，则实数的取值范围是（ ）‎ ‎ A．（-1，0）∪（0，1） B．（-∞，-1）∪（1，+∞）‎ ‎ C．（-1，0）∪（1，+∞） D．（-∞，-1）∪（0，1）‎ ‎12．某学校要召开学生代表大会，规定各班每10人推选一名代表，当各班人数除以10的余数大于6时再增选一名代表，那么，各班可推选代表人数与该班人数之间的函数关系用取整函数表示不大于的最大整数）可以表示为 （ ）‎ ‎ A． B． C． D．‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题（本大题共4小题，每小题4分，共16分）‎ ‎13．已知实数x，y满足条件的最大值为 .‎ ‎14．已知 类比以上等式可推测a，t的值，则a+t = . ‎ ‎15．如图是判断“美数”的流程图，在[30，40]内的所有整数中 ‎“美数”的个数是 。‎ ‎16．O是平面α上一点，点A，B，C是平面α上不共线的三点， ‎ 平面α内的动点P满足 则的值为 。‎ 三、解答题（本大题共6小题，共74分，解答应写出文字说明、‎ 证明过程或演算步骤。）‎ ‎17．（本小题满分12分）‎ 已知 ‎ （I）求的最小正周期和单调递增区间；‎ ‎ （II）在△ABC中，角A满足，求角A。‎ ‎18．（本小题满分12分）‎ 在甲、乙两个盒子中分别装有装号为1、2、3、4的四个小球，现从甲、乙两个盒子中各取出1个小球，每个小球被取出的可能性相等。‎ ‎ （I）求取出两个小球标号恰好相同的概率；‎ ‎ （II）求取出的两个小球的标号至少有一个大于2的概率。‎ ‎19．（本小题满分12分）‎ 已知各项均不相等的等差数列成等比数列。‎ ‎ （I）求数列的通项公式；‎ ‎ （II）设恒成立，求实数的最小值。‎ ‎20．（本小题满分12分）‎ 如图，在四棱锥P—ABCD中，底面ABCD是矩形，平面ABCD，且PA=AD，点F是棱PD的中点，点E在棱CD上移动。‎ ‎ （I）当点E为CD的中点时，试判断直线EF与平面PAC的位置关系，并说明理由；‎ ‎ （II）求证：PE⊥AF。‎ ‎21．（本小题满分12分）‎ 已知椭圆过点，且长轴长等于4。‎ ‎ （I）求椭圆C的方程；‎ ‎ （II）F1，F2是椭圆C的两个焦点，⊙O是以F1，F2为直径的圆，直线与⊙O相切，并与椭圆C交于不同的两点A，B，若的值。‎ ‎22．（本小题满分14分）‎ ‎ 已知函数的一个极值点，且的图象在处的切线与直线平行。‎ ‎ （I）求的解析式及单调区间；‎ ‎ （II）若对任意的都有成立，求函数的最值。‎ ‎2015山东高考数学卷（文科）概念版 胶州实验中学 刘红升 2015.3.6‎ ‎1．灵感来自“李欣芮”，赠于德强老师（二次不等式、复数运算及复数的模）‎ 不等式的解集为：C ‎ ‎2．灵感来自模仿（分段函数）‎ ‎ ‎ ‎3灵感来自“故事”及模仿（统计问题）‎ 山东师范大学98级数学系4班与3班各选5名女同学，将她们的身高数据如下面茎叶图所记录，比较两班女生身高的均值与方差 ‎ 4班 3班 A,4班均值大于3班，4班方差大于3班； ‎ B, 3班均值大于4班，3班方差大于4班；‎ C,3班均值大于4班，4班方差大于3班； ‎ D, 4班均值大于3班，3班方差大于4班 ‎ 6, 6, 3,2, 16 6,7，7‎ ‎ 0 17 0，1‎ ‎ 3 19‎ ‎4．灵感来自“雷锋”及模仿，赠庄志刚老师（数列）‎ 已知数列{}中，，且对任意正整数，，求数列{}的前项和为 ‎ ‎ ‎5．灵感来自“停不住的爱人”，赠罗大佑（函数图像）‎ 对于函数的图像是：‎ ‎ ‎ A. B C D ‎6．灵感来自模仿（向量三角形）‎ 在中，“”是“”的 A,充要条件 B,充分不必要条件 C,必要不充分条件 D,即不充分也不必要条件 ‎7. 灵感来自模仿（函数性质综合：单调、周期、奇偶等）‎ ‎ ‎ ‎8．灵感来自“宝马”汽车标志，赠马拉多纳。（立体几何三视图）‎ 将一个表面为蓝色内部为白色半径为的球等分成部分，切割去几部分后的几何体的三视图如右图，以下关于该几何体的选项正确的是（左面图为正视图，右面为左视图，下面为俯视图）： （注：深色表示蓝色，空白表示白色）‎ A体积为，表面积； B.体积为，表面积； C.体积为，表面积； D.体积为，表面积；‎ ‎ ‎ ‎9. 灵感来自“爱”，赠胶州实验中学（圆、圆、双曲线交汇，双曲线定义、数形结合，把你我的心串一串）‎ 如图：双曲线的左右焦点分别为，圆圆心在原点过双曲线的左右焦点且与双曲线在第一象限的交点为，圆圆心在原点过双曲线的左右顶点且与相切，求双曲线的离心率 ‎ ‎ ‎ ‎10．灵感来自“情书”，赠胶州实验中学全体女教师（逻辑）‎ 某年某月的某一天女生小W过生日，男生小A不知道是哪一天但是想给小W送一封情书在她生日的时候，小A应该那一天送呢？‎ A.“小W的生日是‎5月29日”“的反函数为”是假命题；‎ B. “小W的生日不是‎5月30日”“，否定是： ，”是真命题；‎ C.“若，则小W的生日就是‎5月31日”的否定是真命题；‎ D.“若幂函数的图像过第四象限，则她的生日不是‎6月1日”的否命题是真命题；‎ ‎11．灵感来自“往事只能回味”，赠田明泉老师（几何概型、线性规划）‎ 已知点中随机的到教室的时间，其中，求在方程有实根的概率 ‎ ‎ ‎12．灵感来自“溜溜的她”，赠彭思嘉、苗琼文（基本不等式）‎ 唱片《溜溜的她》销售火爆，公司计划推出限量黄金版《溜溜的她》张（），每张黄金版唱片的价格为：（万元）；每张黄金版唱片的成本为：（万元）；求总利润最大时的值 ‎ ‎13．灵感来自“流水年华”，赠数学与足球（函数零点，三种方法皆可）‎ 有2个零点求实数的范围是 ‎ ‎14．灵感来自模仿（解三角形）中，分别是角的对边，向量，‎ ‎，且，求角B的大小 ‎15．灵感来自模仿（线性规划与框图）‎ 运行图示的程序框图，当输入时的输出结果为．若变量，满足，‎ 开始 ‎?‎ 是 输入p 结束 输出 否 则目标函数：的最大值为___________‎ ‎16. 灵感来自“奥迪”汽车标志，赠巨慧（圆、类比推理）‎ 如图：求两圆的半径均为且一个圆过另一个圆的圆心，‎ 求两圆公共部分（阴影部分）的面积= ；‎ 根据类比推理将圆换成边长为1的两个正方形，其中一 个正方形的一个顶点在两一个正方形的中心，求两正方 形公共部分（阴影部分）的面积= 。 ‎ ‎ ‎ ‎17，本题12分（无灵感来源）‎ 已知函数将函数向左平移后在得函数，（Ⅰ）求的对称中心及单调递增区间；（Ⅱ）若，求值．‎ ‎18.本题12分（灵感来自“情难枕”，赠2011界高三2班）‎ 如下图：已知数列满足：依次成公比为2的等比数列，其余项依次为以 为首项公差为1的等差数列。记的前项和为.‎ ‎ ，‎ ‎ ，‎ ‎。。。。。。。。。‎ ‎ (1)求及（2）求；‎ ‎19.本题12分（灵感来自“北院”，赠孙景涛）‎ 为了了解喜欢数学老师是否与性别有关，对某班20名同学进行问卷调查得到如下22列联表：‎ 喜爱数学老师 不喜爱数学老师 合计 男生 ‎4‎ 女生 ‎8‎ 合计 ‎20‎ ‎（卡方统计量：，其中为样本量。）‎ 已知在全部20人中随机抽取一人，抽到喜爱数学老师的同学的概率为。‎ ‎1.请判断是否有0.99的把握认为喜爱数学老师与性别有关？并说明理由（提示：当时，有0.99的把握说明两事件相关）‎ ‎2.从不喜爱数学老师的男生（含小A）与不喜爱数学老师的女生（含小W）选出3人，这3人中小A和小W均入选的概率。‎ ‎20.本题12分（灵感来自“信”，赠万岱）‎ 下图几何体中,四边形，，。‎ ‎（1）证明：；‎ A B C D E F G ‎（2）探究：线段上是否存在一点满足；‎ 命题灵感“信”‎ ‎21. 本题14分（灵感来自“轮回”“三个火枪手”，赠刘之言）‎ 设函数，函数，‎ ‎（1）证明讨论的单调区间；‎ ‎（2）若，讨论的极值点；‎ ‎22.本题12分（灵感来自“又见溜溜的她” ，赠lilycoffey）‎ 已知椭圆，圆,圆，，‎ ‎（1）若为抛物线上异于原点的两不同点，且；分别为为上不同点，且 。又知：。求直线的方程；‎ ‎（2）椭圆上有两不同点，且。抛物线 上是否存在一点使得： 。若存在求出此定点坐标；若不存在说明理由。‎ ‎2015山东高考数学卷（文科）概念版详解答案 胶州实验中学 刘红升 2015.3.4‎ ‎22.本题12分（灵感来自“又见溜溜的她” ，赠lilycoffey）‎ 已知椭圆，圆,圆，，‎ ‎（1）若为抛物线上异于原点的两不同点，且；分别为为上不同点，且 。又知：。求直线的方程；‎ ‎（2）椭圆上有两不同点，且。抛物线上是否存在一点使得： 。若存在求出此定点坐标；若不存在说明理。‎ ‎（1）（2）组合如图：‎ 命题意图：此题通过直线、圆、椭圆、抛物线与向量交汇的形式作为载体，考察方程思想、数形结合的思想、运算能力、创新意识。其中，方程思想中同时，第一问体现“‎ 乌黑的眼睛溜溜的转”；在考察方程的两种基本方式的同时第二问体现“她”！题目的结果较复杂，如果在设计一下相信结果会比较简单。由于山东理科对于与椭圆要求相同的抛物线已经两年没有涉及，因此本题通过大量抛物线（抛物线系）对抛物线的回归表示期待，至于开口向下完全是为了“形”的构造。还有一些无法用语言表达的东西就用图形来表达吧！‎ 高考背景： 2006年后调整：删去椭圆、双曲线的准线及第二定义；抛物线、双曲线降为了解。目前：椭圆、抛物线并列为“掌握”、双曲线为“了解”。2011年22题：椭圆问题（探究结论、运算求最值、存在性问题探究）；2010年22题：椭圆求方程、直接利用方程证明规律、存在性问题探究；2009年22题：曲线形状讨论、探究圆与椭圆规律、基本弦长运算；2008年22题：求椭圆方程、轨迹方程、面积最值问题；2007年22题：椭圆、圆与椭圆交汇、直线过定点问题探究；2006年21题：椭圆、三角形面积最值问题；2005年22题：抛物线、定义、证明直线过定点问题（方法较多）。由于我们山东解析几何“探究性”明显，如是否存在定点问题等，估计今年还是会通过这种探究性形式命题，考察的本质仍是：方程思想（直接用方程、韦达定理等）、运算能力（运算量大）。至于说圆会不会交汇进来呢？向量呢？其实，向量的坐标转化我们比较熟练，但是向量的几何转化、代数转化我们也不敢说没有问题！至于说圆的进入恐怕为了体现考试说明在圆锥曲线部分中的：“理解数形结合思想”吧！单独说说圆吧！愿承担的使命就是“形”，尽量不要对圆像椭圆一样运算！估计，椭圆回归小题也是必然了，估计会从椭圆的定义（形）上来考察，当然，也不排除椭圆于抛物线交汇的可能，如果说通过抛物线体现“形”加通过椭圆体现数估计也不难命题。我估计今年会在“量与式”的把握上做文章，适当降一下运算量。‎ ‎22.解（1）解析：，‎ ‎（2）解析：设，由可得：‎ ‎21. 本题14分（灵感来自“轮回”“三个火枪手”，赠刘之言）‎ 设函数，函数，‎ ‎（1）证明讨论的单调区间；‎ ‎（2）若，讨论的极值点；‎ 命题意图：‎ 通过对、指、幂函数作为载体，结合单调性、极值、不等证明有机交汇，步步深入，考察学生的分类讨论思想、函数与方程思想、由特殊到一般的思想、数学归纳法等。由于山东高考题中从没有这三个函数交汇的情况，因此命名“三个火枪手”！‎ 高考背景：由于2006年后调整了数列，因此函数代替了数列。2011年21题函数应用题（注意：2007年、2009年、2011年均是2道应用题！而2009年各地一模、二模题目中几乎没有应用题！同样，2011年各地一模、二模题中有极少应用题，不过2010青岛一模20题、二模文科20题，2011年青岛二模20题均是应用题，不要以为“应用意识”是句美丽的口号！）；2010年21题：函数单调性讨论（分类讨论思想现在改称“分类整合”）、求切线方程；2009年21题：函数极值、单调性讨论、恒成立不等证明；2008年21题：单调性讨论，不等证明；2007年21题：函数极值；2006年17题：函数单调性、求极值；2005年19题：函数单调性讨论；我觉得：函数使用上理科基本放弃3次函数，对数函数很受“器重”！我猜：对、指、幂会不会同时出现？还有我们平时做的含参恒成立（首推“分离参数”这是一种“转化化归”思想）考查的并不多，因为一旦分离便不好考查“分类整合”思想了，只有2009年文科21题体现了恒成立问题。我个人相对欣赏2007年的形式，如果2015年函数21题（极可能）的话，2007年高考题值得研究。总体感觉6年函数题恰恰在“函数与方程”思想上考察的不很明确，会调整吗？如何调整呢？‎ ‎21解：（1）证明 ‎。。。。。。。。。。。。。。6分；‎ ‎（2）‎ ‎，‎ 此时，由上问知：，无极值点；。。。。。。。。。。。。。。。。。。。。。。8分；‎ 此时，由上问知：，无极大值点；极小值点为。。。。。。。。。。。。。。。。。。。。。。。12分 命题灵感：轮回 轮回 越来越多无所从来的魔，‎ 越来越多从天而降的佛，‎ 越来越黑像夜一样美，‎ 越来越美姑娘的眼泪 十二道的轮回大千的世界，‎ 只要你尽力而为 看见一道光 ‎ 从天而降 ‎ 随孽而转 ‎20.本题12分（灵感来自“信”，赠万岱）‎ 下图几何体中,四边形，，。‎ ‎（1）证明：；‎ A B C D E F G ‎（2）探究：线段上是否存在一点满足；‎ 命题灵感“信”‎ 命题意图：通过“信”（俯视图）作为载体通过平行、垂直问题的证明与探究重点考察空间想想能力、运算能力等。由于设计时间急促未能将平行问题及线面角问题涉及。当然，此题也带有一些“羞涩的回忆”。因此只能够在小题中补充考察未能考察的方面。‎ 高考背景：偶数年以锥体为载体、奇数年以柱体为载体。偶数年平行、奇数年垂直，当然这些“规律”在今年被打破，其实立体几何大要求摆在那里，什么载体真的不重要。2011年19题：线线垂直、线面平行；2010年20题：面面垂直、体积问题；2009年18题：线面平行、面面垂直；2008年19题：面面垂直、体积问题；2007年20题：线线角、二面角、线面垂直；2006年19题：公垂线证明（已删）、点面距离（已删）、二面角；2005年20题：线线角、二面角（涉及线面角）、点面距离（已删）。总之：2006年后删去空间距离、球面距离、球的切接问题等添加了三视图、投影等知识后明显降低了立体几何的难度，但是大题难度变化不太大。关于空间距离：已经删了。不过由于体积问题与空间距离有一定联系所以令人头痛，我觉得不应作为重点，相信体积问题的高不会难求而且我们可以等体积转化！关于球的切接问题我认为坚决不要搞了!不是已经删了吗？？？纵观6年高考线线角大小题只考了一次！线线角大小题考了3次！二面角考了5次！体积考了1次。‎ 春夏秋冬 你似微风吹醒我心灵，羞怯还带着惊喜，默默递给我一朵小野花，带给我喜悦的春 你伴着我带着老吉他，吟唱在山颠水涯，深情注视我笑在艳阳下，漫溢我欢畅的夏 你难忘记流浪的岁月，挥挥手只留下背影，弹着老吉他我依然吟唱，潇洒我清愁的秋 你已远去无处觅游踪，寄语浮云传珍重，多情应似我此情与谁共，凋零我孤寂的冬 G A B C D E F ‎20解：‎ ‎（1）（1）如图：‎ ‎（2）‎ 存在点 如右图做辅助线。‎ A B C D E F ‎。‎ G 命题灵感“信”‎ ‎19.本题12分（灵感来自“北院”，赠孙景涛）‎ 为了了解喜欢数学老师是否与性别有关，对某班20名同学进行问卷调查得到如下22列联表：‎ 喜爱数学老师 不喜爱数学老师 合计 男生 ‎4‎ 女生 ‎8‎ 合计 ‎20‎ ‎（卡方统计量：，其中为样本量。）‎ 已知在全部20人中随机抽取一人，抽到喜爱数学老师的同学的概率为。‎ ‎（1）请判断是否有0.99的把握认为喜爱数学老师与性别有关？并说明理由（提示：当时，有0.99的把握说明两事件相关）‎ ‎（2）从不喜爱数学老师的男生（含小A）与不喜爱数学老师的女生（含小W）选出3人，这3人中小A和小W均入选的概率。‎ 命题灵感：‎ 北院。‎ 命题意图：‎ 通过独立性检验、概率独立、超几何分布、排列组合为载体考察分类讨论等数学思想及运算能力！‎ 高考背景：‎ ‎2011年18题独立事件的概率；2010年20题（不放回）独立事件概率（实际生活背景明显）、分类讨论思想；2009年19题（不放回独立）涉及积事件（是否独立）概率等；2008年18题（不放回独立）涉及二项分布、积事件（是否独立）概率等；2007年18题：古典概型（结合二次方程）、条件概率（这是条件概率进入高中来唯一考查的一次，今年该考了！），当时条件概率出错极多，而且考试说明对条件概率要求“了解”，因此我觉得2015年会考一道小题。总体上我觉得概率题目的实际生活背景在加强。注意：对数学期望、方差的实际意义考查很少，今年会涉及吗？还有，将统计等知识交汇于概率解答题中是很好的载体（不排除独立性检验等进入解答题，如：2011年潍坊二模概率题）。‎ ‎19解：（1）填表如下：‎ 喜爱数学老师 不喜爱数学老师 合计 男生 ‎6‎ ‎4‎ ‎10‎ 女生 ‎8‎ ‎2‎ ‎10‎ 合计 ‎14‎ ‎6‎ ‎20‎ 由题知：，所以没有0.99的把握认为喜爱数学老师与性别有关 ‎（2）‎ 红尘有你 我心的空间是你走过以后的深渊 我情的中间是你留下回忆的片段 我梦的里面是场流离失所的演变 我泪的背面依然留着等你的天 红尘有你就有我无悔的泥 走过人间千百回天涯又回到深情的原点 那岁月再怎么摧残我的心不会怕永远 因为梦和爱不会忘记，‎ 红尘有你 ‎18.本题12分（灵感来自“情难枕”，赠2011界高三2班）‎ 如下图：已知数列满足：依次成公比为2的等比数列，其余项依次为以 为首项公差为1的等差数列。记的前项和为.‎ ‎ ， ，。。。。。。。。。‎ ‎ (1)求及 ‎（2）求；‎ 命题灵感：大学毕业10年，因此以10作为周期。‎ 命题意图：在具体情境中识别等差等比关系并解决相应问题，通过通项与求和重点考察等差等比数列。‎ 高考背景：2011年20题：等比数列，求和； 2010年18题：等差数列及裂项求和；2009年20题：等比数列问题（涉及母子关系）、错位相减求和；2008年20题：涉及“母子关系”、图表数列题（此题令人对考试说明中“能再具体情境中识别等差等比关系”令人黯然销魂！我觉得：图表数列、分段数列、数列应用题是“具体情境”的很好载体！如：污水处理、甲壳虫等题）、等比数列问题。2007年19题：等差数列、求和问题；2006年22题：构造新数列（提示）、叠加求通项、求和；2005年21题：构造新数列（提示）、等比数列求和。应该说7年错位相减考了2次（或3次），文科也考了2次（或3次），我依然对“数列应用题”充满期望！总体来说数列的地位已经降低，解答题最多20题，小题可有可无，这就是目前数列的地位，2015会改变吗？‎ 故事 我们在雨中别离 说不定又会在风中相遇 白云说邂逅是一种伤心的美丽 就像那躲进河流的雨滴 终于你剪了长发 也终于我把相片都拆下 岁月说签名和留影都会被遗忘 谁不学不流泪谁是傻瓜 我们匆匆的来又匆匆的去 倔强的青春不就是一只脆弱的琉璃 我们匆匆的来又匆匆的去 在天涯留下寻梦的跫音 流浪以后才明白对你有一份痴心 慢慢学会了牵挂怕你哭泣没人理 当你开始怀念我的从前 故事会不会改变 ‎17，本题12分（无灵感来源）‎ 已知函数将函数向左平移后在得函数，‎ ‎（Ⅰ）求的对称中心及单调递增区间；‎ ‎（Ⅱ）若，求值．‎ 命题意图：通过诱导公式、一角一函数、平移等基本载体考察三角函数图像性质及化简求值。‎ 高考背景：2011年为解三角形问题。2010年17题考查三角函数图像性质及平移；2009年考查三角函数图像性质结合解三角形；2008年考查三角函数图象性质及平移；2007年通过应用题考查解三角形；2006年考查三角形图像性质；2005年考查三角函数化简求值并与向量结合。应该说今年最大可能是解三角形问题（这是三角部分唯一考试说明要求“掌握”的内容）；另外老师们比较担心“三角化简求值”，往往对公式熟练及运算要求较高。估计前者可能性最大。‎ ‎17：解： ‎ ‎。。。。。。。。。。。。。。。。。。。。。。。。。。。。。1分 ‎ ‎ ‎(2)‎ ‎1．灵感来自“李欣芮”，赠于德强老师（绝对值不等式、复数）‎ 不等式的解集为：C ‎ ‎ ‎ ‎ ‎2．灵感来自模仿（分段函数）‎ C ‎3灵感来自“故事”及模仿,（统计问题）‎ 山东师范大学98级数学系4班与3班各选5名女同学，将她们的身高数据如下面茎叶图所记录，比较两班女生身高的均值与方差C ‎ 4班 3班 ‎ 6, 6, 3,2, 16 6,7，7‎ ‎ 0 17 0，1‎ ‎ 3 19‎ A,4班均值大于3班，4班方差大于3班； B, 3班均值大于4班，3班方差大于4班；‎ C,3班均值大于4班，4班方差大于3班； D, 4班均值大于3班，3班方差大于4‎ 班；‎ ‎4．灵感来自“雷锋”及模仿，赠庄志刚老师（数列）‎ 已知数列{}中，，且对任意正整数，，求数列{}的前项和为D ‎ ‎ ‎5．灵感来自函数图像 对于函数的图像是：A ‎ ‎ A. B C D ‎6．灵感来自模仿（向量三角形）‎ 在中，“”是“”的A A,充要条件 B,充分不必要条件 C,必要不充分条件 D,即不充分也不必要条件 ‎7. 灵感来自模仿（函数性质综合：单调、周期、奇偶等）‎ C ‎ ‎8．灵感来自“宝马”汽车标志，赠马拉多纳。（立体几何三视图）‎ 将一个表面为蓝色内部为白色半径为的球等分成部分，切割去几部分后的几何体的三视图如右图，以下选项正确的是（左面图为正视图，右面为左视图，下面为俯视图）：A A.该几何体的体积为，表面积为； B. 该几何体的体积为，表面积为；‎ C. 该几何体的体积为，表面积为； D. 该几何体的体积为，表面积为；‎ ‎（注：深色表示蓝色，空白表示白色） ‎ ‎9. 灵感来自“爱”，赠胶州实验中学（圆、圆、双曲线交汇，双曲线定义、数形结合，把你我的心串一串）‎ 如图：双曲线的左右焦点分别为，圆圆心在原点过双曲线的左右焦点且与双曲线在第一象限的交点为，圆圆心在原点过双曲线的左右顶点且与相切，求双曲线的离心率 D ‎ ‎ ‎ ‎ ‎10．灵感来自“情书”，胶州实验中学全体女教师（逻辑）‎ 某年某月的某一天女生小W过生日，男生小A不知道是哪一天但是想给小W送一封情书在她生日的时候，小A应该那一天送呢？D A.“小W的生日是‎5月29日”“的反函数为”是假命题；‎ B. “小W的生日不是‎5月30日”“，否定是： ，”是真命题；‎ C.“若，则小W的生日就是‎5月31日”的否定是真命题；‎ D.“若幂函数的图像过第四象限，则她的生日不是‎6月1日”的否命题是真命题；‎ ‎11．灵感来自“往事只能回味”，赠田明泉老师（几何概型、线性规划）‎ 已知点中随机的到教室的时间，其中，求在方程有实根的概率D ‎ ‎ ‎12．灵感来自“溜溜的她”，赠彭思嘉、苗琼文（基本不等式）‎ 唱片《溜溜的她》销售火爆，唱片公司计划推出限量黄金版《溜溜的她》张（），每张黄金版唱片的价格为：（万元）；每张黄金版唱片的成本为：（万元）；求总利润最大时的值B ‎ ‎ ‎13．灵感来自“流水年华”，赠数学与足球（函数零点，三种方法皆可）‎ 有2个零点求实数的范围是 ‎ ‎14．灵感来自模仿（解三角形）‎ 开始 ‎?‎ 是 输入p 结束 输出 否 中，分别是角的对边，向量，，且，求角B的大小 ‎ ‎15．灵感来自模仿（线性规划与框图）‎ 运行图示的程序框图，当输入时的输出 结果为．若变量，满足，‎ 则目标函数：的最大值为___________‎ ‎16. 灵感来自“奥迪”汽车标志，赠巨慧（圆、类比推理）‎ 如图：求两圆的半径均为且一个圆过另一个圆的圆心，求两圆公共部分（阴影部分）的面积= ；根据类比推理将圆换成边长为1的两个正方形，其中一个正方形的一个顶点在两一个正方形的中心，求两正方形公共部分（阴影部分）的面积= 。 ‎ ‎ ‎ ‎2015山东高考数学卷（文科）概念版简解答案 ‎1---12CCCDA ACADD DB ‎13： 14： 15:5 16：‎ ‎17：解： ‎ ‎ ‎ ‎(2)‎ ‎18解：（1）由题意知：；‎ ‎(2)‎ ‎19解：（1）填表如下：‎ 喜爱数学老师 不喜爱数学老师 合计 男生 ‎6‎ ‎4‎ ‎10‎ 女生 ‎8‎ ‎2‎ ‎10‎ 合计 ‎14‎ ‎6‎ ‎20‎ 由题知：，所以没有0.99的把握认为喜爱数学老师与性别有关 A B C D E F G ‎（2）‎ ‎20解：‎ ‎（1）（1）如图：‎ A B C D E F ‎（2）‎ 存在点 如右图做辅助线。‎ ‎。‎ G ‎21解：（1）证明 ‎。。。。。。。。。。。。。。6分；‎ ‎（2）‎ ‎，‎ 此时，由上问知：，无极值点；。。。。。。。。。。。。。。。。。。。。。。8分；‎ 此时，由上问知：，无极大值点；极小值点为。。。。。。。。。。。。。。。。。。。。。。。12分 ‎22.解（1）解析：，‎ ‎（2）解析：设，由可得：‎ ‎ 高考冲刺卷（六）‎ 文科数学 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟．‎ 第Ⅰ卷（选择题，共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只 ‎ 有一项是符合题目要求的．‎ ‎1．设全集，则是 A． B．或 C． D．且 ‎2．己知复数满足，则等于 A． B． C． D．‎ ‎3．设等差数列的前项和为，若，则 A．63 B．‎45 ‎ C．36 D．27‎ ‎4．设、是不同的直线，、、是不同的平面，有以下四个命题：‎ ‎① 若，则 ② 若，则 ‎③ 若，则 ④ 若，则 其中真命题的序号是 A．①④ B．②③ C．②④ D．①③‎ ‎5．已知，则的值为 A． B． C． D．‎ ‎6．是的展开式中含的项的系数，则 A．1 B．‎2 ‎ C．3 D．4‎ ‎7．设双曲线的离心率为，且它的一条准线与抛物线的 ‎ 准线重合，则此双曲线的方程为 A． B． C． D．‎ ‎8．的展开式中的系数是 A． B． C．3 D．4‎ ‎9．从4名男生和3名女生中选出3人，分别从事三项不同的工作，若这3人中有且只有1‎ ‎ 名女生，则选派方案共有 A．108种 B．186种 C．216种 D．270种 ‎10．已知是上的增函数，那么的取值范围是 A． B． C． D．（1，3）‎ ‎11．设奇函数在上为增函数，且，则不等式解集 ‎ 为 A． B．‎ C． D．‎ ‎12．是定义在上的非负可导函数，且满足，对任意正数、‎ ‎ 若，则必有 A． B．‎ C． D．‎ 第Ⅱ卷（非选择题，共90分）‎ 二、填空题：本大题共4小题。每小题5分．共20分．把答案填在题中横线上．‎ ‎13．在某项测量中，测量结果服从正态分布，若在在（0，1）内取值的 ‎ 概率为0．4，则在（0，2）内取值的概率为 ．‎ ‎14．平面上的向量满足，且，若向量,‎ ‎ 则的最大值为 。‎ ‎15．在正方体中，与平面所成的角为 ．‎ ‎16．给出下列3个命题：‎ ‎① 命题“存在”的否定是“任意”；‎ ‎② “”是“直线与直线相互垂直”的必要不充分条件；‎ ‎③ 关于的不等式的解集为，则．‎ 其中为真命题的序号是 ．‎ 三、解答题：本大题共6小题。共70分．解答应写出文宇说明、证明过程或演算步骤．‎ ‎17．（本小题满分12分）‎ 已知函数的最小正周期为．‎ ‎（1）求的单调递增区间；‎ ‎（2）在中，角，，的对边长分别是，，满足，求函数的取值范围．‎ ‎18．（本小题满分12分）‎ 有编号为l，2，3，…，的个学生，入坐编号为1，2，3，…，的个座位．每个学生规定坐一个座位，设学生所坐的座位号与该生的编号不同的学生人数为，已知时，共有6种坐法．‎ ‎（1）求的值；‎ ‎（2）求随机变量的概率分布列和数学期望．‎ ‎19．（本小题满分12分）‎ 已知数列是其前项和，且．‎ ‎（1）求数列的通项公式；‎ ‎（2）设是数列的前项和，求使得对所有都成立的最小正整数。‎ ‎20．（本小题满分12分）‎ 已知四棱锥的底面是正方形，且底面，其中．‎ ‎（1）求二面角的大小；‎ ‎（2）在线段上是否存在一点，使平面．若存在，试确定点的位置；若不存在，请说明理由．‎ ‎21．（本小题满分10分）‎ 已知椭圆，过焦点垂直于长轴的弦长为l，且焦点与短轴两端点构成等边三角形．‎ ‎（1）求椭圆的方程；‎ ‎（2）过点的直线交椭圆于，两点，交直线于点，点分所成比为，点分所成比为，求证为定值，并计算出该定值．‎ ‎22．（本小题满分12分）‎ 已知函数．‎ ‎（1）若在上是减函数，求的取值范围；‎ ‎（2）函数是否既有极大值又有极小值?若存在，求的取值范围；若不存在，请说明理由．‎ 参考答案 一、‎ ‎1．C 2．D 3．B 4．D 5．D 6．B 7．D 8．A 9．A 10．C ‎ ‎11．D 12．A ‎1～11．略 ‎12．解：，‎ ‎ 在是减函数，由，得，，故选A．‎ 二、‎ ‎13．0．8 14． 15． 16．①③‎ 三、‎ ‎17．解：（1）‎ ‎ ‎ ‎ 的单调递增区间为 ‎ （2）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎18．解：（1）当时，有种坐法，‎ ‎ ，即，‎ ‎ 或舍去． ‎ ‎ （2）的可能取值是0，2，3，4‎ ‎ 又 ‎ ‎ ‎ 的概率分布列为 ‎ ‎0‎ ‎2‎ ‎3‎ ‎4‎ ‎ 则．‎ ‎19．解：（1）时，，‎ ‎ ‎ ‎ 又 ，‎ ‎ ‎ ‎ 是一个以2为首项，8为公比的等比数列 ‎ ‎ ‎ （2）‎ ‎ ‎ ‎ 最小正整数．‎ ‎20．解法一：‎ ‎ （1）设交于点 ‎ 平面．‎ 作于点，连接，则由三垂线定理知：是二面角的平面角．‎ 由已知得，‎ ‎，‎ ‎∴二面角的大小的60°．‎ ‎ （2）当是中点时，有平面．‎ ‎ 证明：取的中点，连接、，则，‎ ‎ ，故平面即平面．‎ ‎ 又平面，‎ ‎ 平面．‎ 解法二：由已知条件，以为原点，以、、为轴、轴、轴建立空间直角坐标系，则 ‎ ‎ ‎ （1），‎ ‎ ，设平面的一个法向量为，‎ 则取 设平面的一个法向量为，则取．‎ 二面角的大小为60°．‎ ‎（2）令，则，‎ ‎ ，‎ ‎ 由已知，，要使平面，只需，即 则有，得当是中点时，有平面．‎ ‎21．解：（1）由条件得，所以椭圆方程是．‎ ‎ ‎ ‎（2）易知直线斜率存在，令 ‎ 由 ‎ ‎ ‎ 由，‎ 即得 ‎，‎ 即 得 将代入 ‎ 有 ‎22．解：（1）‎ ‎ 在上为减函数，时，恒成立，‎ ‎ 即恒成立，设，则 ‎ 时，在（0，）上递减速，‎ ‎ ‎ ‎ ．‎ ‎（2）若即有极大值又有极小值，则首先必需有两个不同正要，，‎ ‎ 即有两个不同正根 ‎ 令 ‎ ∴当时，有两个不同正根 ‎ 不妨设，由知，‎ ‎ 时，时，时，‎ ‎ ∴当时，既有极大值又有极小值．‎ ‎2015年高考文科数学模拟试卷1‎ 卷Ⅰ客观题 一、选择题：10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎(1) 设U=R，集合，则下列结论正确的是 ‎ A B ‎ C D ‎ 开始 S=0，i=0‎ S=S+2i-1‎ i≥8‎ i=i+2‎ 结束 输出S 否 是 ‎（2）已知，复数，若为纯虚数，则复数的虚部为 ‎ ‎ A 1 B C D 0 ‎ ‎（3）已知函数有唯一零点，则存在零点的区间是 ‎ A B C D ‎(4) 右图的程序框图输出结果S=‎ ‎ A 20 B 35‎ ‎ C 40 D 45‎ ‎(5) 设F是椭圆的右焦点，椭圆上的点与点F的最大距离为M，最小距离为N，则椭圆上与点F的距离等于的点的坐标是 ‎ A B C D ‎ ‎(6) 在中，设命题,命题是等边三角形，那么命题是命题的 A 充分不必要条件 B 必要不充分条件 C 充分必要条件 D 既不充分又不必要条件 ‎（7）已知等差数列和的前n项和分别为和，且，则使得为整数的正偶数时，n的值是 ‎ A 1 B 3或‎11 C 5 D 2‎ ‎(8) 若对于，不等式恒成立，则正实数的取值范围为 ‎ A B C D ‎ ‎（9）已知m、n是不同的直线，、β是不同的平面，下列命题中真命题的个数为 ‎①//β,,则//； ‎ ‎ ②,//,则； ‎③，//，//，则；‎ ‎④若与异面直线，，//β，//β，则//β。‎ A 0 B ‎1 ‎‎ ‎‎ C 2 D 3 ‎（10）设非空集合满足：当时，有。给出如下三个命题：①若，则；②若，则；③若，则。其中正确命题的个数是 A 0 B ‎1 ‎ C 2 D 3‎ 卷Ⅱ主观题 二、填空题：本大题共7小题，每小题4分，共28分。‎ ‎（11）某单位200名职工的年龄分布情况如下图，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1－200编号，并按编号顺序平均分为40组（1－5号，6－10号…，196－200号）.若第5组抽出的号码为22，则第8组抽出的号码应是 。若用分层抽样方法，则40岁以下年龄段应抽取 人. ‎ ‎ ‎ ‎（12）一个几何体的三视图如图所示：其中，正视图中△ABC的边长是2的正三角形，俯视图为正六边形，那么该几何体的体积为 .‎ ‎(第14题)‎ H G F E D C B A ‎（13）若直线与圆相交于A,B两点，则弦AB长的最小值为__________.‎ ‎（14）如图，已知矩形ABCD，AB＝2，AD＝1．若点E，F，G，H 分别在线段AB，BC，CD，DA上，且AE＝BF＝CG＝DH，‎ 已知以EFGH为底面的四棱锥高为3，则四棱锥体积的 最小值为________.‎ ‎（15）已知是两个非零向量，且，则与 的夹角大小为_________.‎ ‎(16) 设是定义在实数R上的以3为周期的奇函数，若，则实数的取值范围为_________.‎ ‎(17) 过点作直线与圆相交，在弦长均为整数的所有直线中，等可能的任取一条直线，则长度超过的概率为 __ .‎ 三、解答题：共5小题，18—20题每题14分，21—22题每题15分，共72分。解答应写出文字说明。‎ ‎(18) (本题满分14分) 设的内角所对的边长分别为，且 ‎．‎ ‎（1）求角的大小； ‎ ‎（2）若角，边上的中线的长为，求的面积．‎ ‎(19) (本题满分14分)设数列的前n项和为Sn=2n2，为等比数列，且 ‎（Ⅰ）求数列和的通项公式； ‎ ‎（Ⅱ）设，求数列的前n项和 ‎(20) (本题满分14分) 已知与都是边长为 的等边三角形，且平面平面，过点作平面，且．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求直线与平面所成角的大小．‎ ‎(21) （本小题满分15分）已知函数 ．‎ ‎ （Ⅰ）当时，判断函数在上的单调性，并证明你的结论；‎ ‎ （Ⅱ）若是函数的两个不同的极值点，且，求实数的取值范围.‎ ‎(22) 已知抛物线：上一点到其焦点的距离为．‎ ‎ （I）求与的值；‎ ‎ （II）设抛物线上一点的横坐标为，过的直线交于另一点，交轴于点，过点M作抛物线的切线MN，N（非原点）为切点，以MN为直径作圆A，若圆A恰好经过点Q，求的最小值．‎ y M P QQ N x O 试卷设计说明 题型 题号 试题来源 内容领域/知识内容 知识深度 测量目标/行为目标 预估难度 单选题 ‎1‎ 课本习题改编 集合 理解 应用 ‎0.85‎ ‎2‎ 课本习题改编 复数运算 掌握 应用 ‎0.85‎ ‎3‎ 原创 零点存在定理 了解 判断 ‎0.85‎ ‎4‎ 原题引用 程序框图 理解 应用 ‎0.8‎ ‎5‎ 原创 椭圆 掌握 总结 ‎0.7‎ ‎6‎ 改编自10高考上海卷18题 逻辑 理解 判断 ‎0.7‎ ‎7‎ 课本习题改编 数列 掌握 分析 ‎0.65‎ ‎8‎ 改编自宁波八校联考卷17题 基本不等式 掌握 组织 ‎0.65‎ ‎9‎ 课本习题改编 点线面 理解 判断 ‎0.75‎ ‎10‎ 改编自杭十四中月考卷第10题 集合与函数 理解 核查 ‎0.6‎ 填空题 ‎11‎ 原题引用 抽样 了解 识记 ‎0.95‎ ‎12‎ 原题引用 三视图 理解 识记 ‎0.75‎ ‎13‎ 改编自2011高考样卷第12题 直线与圆 理解 应用 ‎0.75‎ ‎14‎ 改编自2011高考样卷第15题 函数的最值 掌握 组织 ‎0.7‎ ‎15‎ 改编自2011高考样卷第14题 向量 理解 归纳 ‎0.75‎ ‎16‎ 原创 函数性质 理解 组织 ‎0.65‎ ‎17‎ 改编自宁波市期末卷第16题 概率 理解 应用 ‎0.6‎ 解答题 ‎18‎ 改编自温州五校联考第18题 解三角形 掌握 应用 ‎0.7‎ ‎19‎ 改编自宁波八校联考卷19题 数列的通项公式及错位相减法求和 掌握 应用 ‎0.7‎ ‎20‎ 改编自温州十校联合第20题 立体几何 理解 应用 ‎0.7‎ ‎21‎ 改编自杭高月考卷第22题 导数 理解 分析 ‎0.6‎ ‎22‎ 解析几何 掌握 分析 ‎0.6‎ 改编自09高考浙江卷 ‎2011年浙江省普通高中高考模拟试卷(数学文科)参考答案 一、选择题：本大题共10小题，每小题5分，共50分 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 C A C A B C B B A D 二、填空题：本大题共7小题，每小题4分，共28分 ‎11． 37 , ___20____ 12． 13．___ 14． ‎ ‎15． 16． 17． ‎ 三、解答题：本大题共5小题，共72分，解答应写出文字说明，证明过程或演算步骤。‎ ‎(18) （Ⅰ）因为，‎ 所以 ‎， 则，‎ 所以，于是 …………7分 ‎ （II）由（Ⅰ）知，所以， ‎ ‎ 设，则 ‎ 又 ‎ ‎ 在中由余弦定理得 ‎ 即 ‎ 解得故 …………14分 ‎（19）（Ⅰ）当……………………………………………………1分 ‎……………………………‎ ‎3分 ‎ 故{an}的通项公式为的等差数列.………………5分 设{bn}的通项公式为 故……………………7分 ‎（II）………………………………………………9分 ‎………………11分 两式相减得 ‎………14分 ‎(20) （Ⅰ）取的中点，连接，则 又∵平面平面，∴平面．‎ 而平面，∴，又∵在平面内， ‎ ‎∴平面． ……6分 ‎（Ⅱ）∵在平面的射影是，在平面的射影是 ，‎ ‎∴在平面的射影是，即直线与 平面 所成角就是直线与直线 所成的角， ……9分 过作交于，由（Ⅰ）可知，‎ ‎∴‎ ‎∴‎ 即 ……14分 ‎(21) （Ⅰ）当时，，则 ‎ 而方程的判别式恒成立，所以恒成立，即函数在上的单调递增． ……5分 ‎（II）∵，∴．‎ 是函数的两个不同的极值点，则是方程的两个不同的实数根，‎ ‎ 即，且 ‎∵，即 ‎∴，即，则 即 ……10分 又 ‎（舍）‎ 当时，，函数是增函数；‎ 当时，，函数是减函数；‎ 当时，函数取到最大值 所以． ……15分 ‎（22）（Ⅰ）由抛物线方程得其准线方程：，根据抛物线定义 点到焦点的距离等于它到准线的距离，即，解得 抛物线方程为：，将代入抛物线方程，解得 ……4分 ‎ ‎（Ⅱ）由题意知，过点的直线斜率存在且不为0，设其为。‎ 则，当 则 ……6分 ‎ 联立方程，整理得：‎ 即：，解得或 ‎ ……8分 ‎ 而以MN为直径的圆A恰好经过点Q ‎，直线斜率为 ‎，联立方程 整理得：，即：‎ ‎ ，解得：，或 ‎， ……12分 ‎ 而抛物线在点N处切线斜率：‎ MN是抛物线的切线，， 整理得 ‎，解得（舍去），或， ……15分 ‎ www.zxsx.com