高考数学文一轮复习第十次测试

高考数学文一轮复习第十次测试

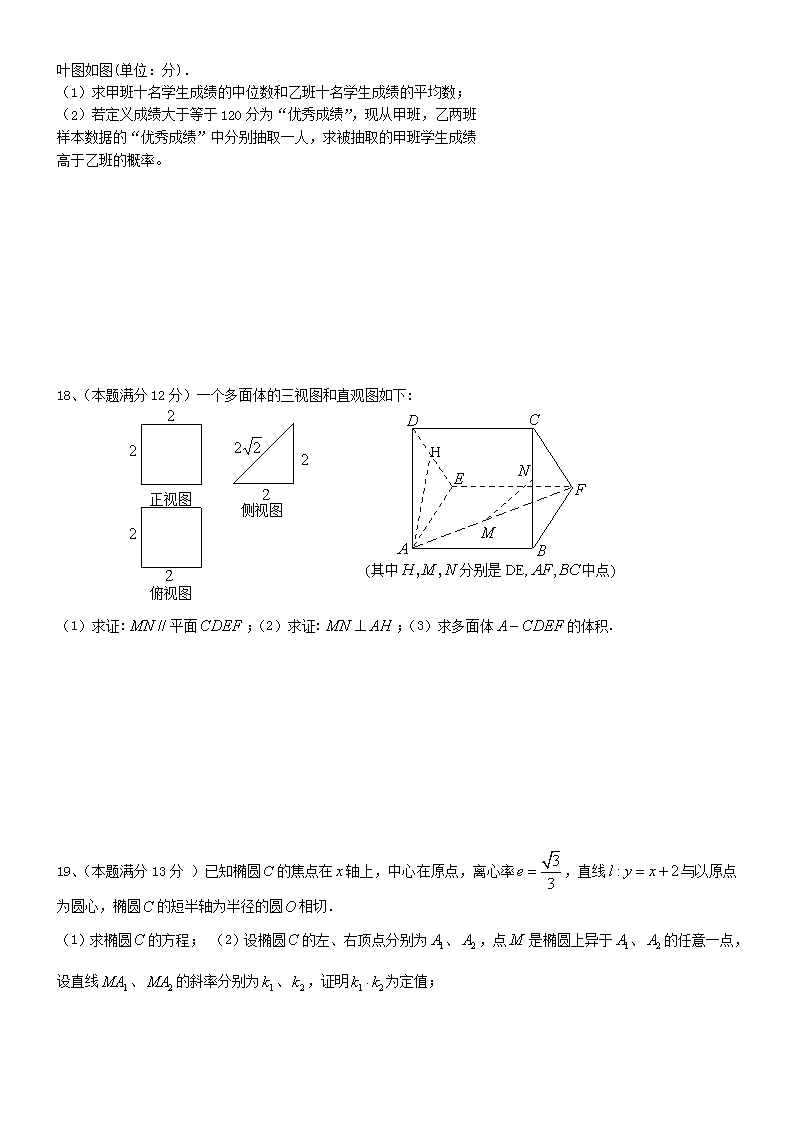
y x2πO A 1 1 D y x2πO 1 1 B y x2πO 1 1 C y x2πO 1 1 开始 输入 ba, ？ba ≤ 输出 a b 1− 输出 b a 1+ 结束 是 否 2013 届高考数学（文）一轮复习第十次测试 一、选择题：本大题共 10 小题，每小题 5 分，满分 50 分. 1.设全集 U= ，定义： ，集合 A，B 分别用圆表示，则下列图中阴影部分 表示 A—B 的是 2. 如果复数 为纯虚数,则实数 a 的值 A. 1 B. 2 C. 1 或 2 D.不存在 3. 已知 是单位向量，且 夹角为 60°，则 等于 A．1 B． C．3 D． 4.在同一个坐标系中画出函数 的部分图象，其中 ，则下列所给图象中可能 正确的是 5. 等差数列 的前 项和为 ，那么 值的是 A．65 B．70 C．130 D．260 6．若 且 ,则下列不等式恒成立的是 A． B． C． D． 7.下面给出四个命题中正确的命题是 ①若平面 //平面 ， 是夹在 间的线段，若 // ，则 ； ② 是异面直线， 是异面直线，则 一定是异面直线； ③过空间任一点，可以做两条直线和已知平面 垂直； ④平面 //平面 ， ， // ，则 。 A．①④ B．①② C．①②③ D．①②④ 8.已知数列 为公比是 3 的等比数列，前 n 项和 ，则实数 为 A．0 B．1 C． D．2 9.对任意非零实数 ， ，若 的运算规则如右图的程序框图所示，则 的值是 A B∪ { | , }A B x x A x B− = ∈ ∉且 2( 3 2) ( 1)z a a a i= + +－ － | | 2,a b=  a b 与 ( )a a b⋅ −   2 3− 4 3− , sinxy a y ax= = 0 1a a> ≠且 }{ na n 30, 1191 =++ aaaSn 若 13S 0, 0,a b> > 4=+ ba 2 11 > ab 111 ≤+ ba 2≥ab 2 2 8a b+ ≥ α β ,AB CD ,α β AB CD AB CD= ,a b ,b c ,a c α α β P α∈ PQ β PQ α⊂ }{ na kS n n += 3 k 1− a b a b⊗ (3 2) 4⊗ ⊗ A B C A B A A B B A B D 10 11 12 8 2 3 3 2 1 8 2 1 1 7 9 9 3 4 8 0 2 7 8 甲 乙 A.0 B. C. D.9 10.一个几何体的正视图、侧视图、俯视图如图所示，则该几何体的表面积和体积 分别为 A． B． 和 C． 　　 D． 题号 1 2 3 4 5 6 7 8 9 10 答案 二、填空题：本大题共 5 小题，每小题 5 分，满分 25 分. 11.已知直线 及 与函数 图像的交点分别为 ，则直线 AB 方程为 12.点 A（3，1）和 B（-4，6）在直线 的两侧，则 a 的取值范围是 。 13.有一个各棱长均为 1 的正四棱锥，先用一张正方形包装纸将其完全包住，不能剪裁，可以折叠，那么包装纸 的最小面积为 14.已知函数 ， ， ，则 的最小值等于 15.一名小学生的年龄和身高（单位：cm)的数据如下： 年龄 x 6 7 8 9 身高 y 118 126 136 144 由散点图可知，身高 y 与年龄 x 之间的线性回归直线方程为 ，预测该学生 10 岁时的身高为 参考公式：回归直线方程是： 三、解答题：本大题共 6 小题，满分 75 分.解答须写出文字说明、证明过程和演算步骤. 16、（本题满分 12 分）已知向量 ， ，定义 （1）求函数 的表达式，并求其单调增区间； （2）在锐角△ABC 中，角 A、B、C 对边分别为 、 、 ，且 ， ，求△ABC 的面积． 17、（本题满分 12 分）为调查某次考试数学的成绩，随机抽取某中学甲、乙两班各十名同学，获得成绩数据的茎 1 2 3 2 42 2 2 4 3 π π π+ + 和 2 2 2π π+ 4 3 π 42 2 3 π π和 82 2 3 π π和 2x = 4x = 2logy x= ,A B 3 2 0x y a− + =  8.8y x a= + ( 2sin , 1 )m x= − − ( cos , cos2 )n x x= − ( )f x m n= ⋅  )(xf a b c 1)( =Af 8=bc ( ) | lg |f x x= 0a b> > ( ) ( )f a f b= 2 2a b a b + −   ,y bx a a y bx= + = −  叶图如图(单位：分)． （1）求甲班十名学生成绩的中位数和乙班十名学生成绩的平均数； （2）若定义成绩大于等于 120 分为“优秀成绩”，现从甲班，乙两班 样本数据的“优秀成绩”中分别抽取一人，求被抽取的甲班学生成绩 高于乙班的概率。 18、（本题满分 12 分）一个多面体的三视图和直观图如下: （1）求证: 平面 ；（2）求证: ；（3）求多面体 的体积. 19、（本题满分 13 分 ）已知椭圆 的焦点在 轴上，中心在原点，离心率 ，直线 与以原点 为圆心，椭圆 的短半轴为半径的圆 相切． （1）求椭圆 的方程； （2）设椭圆 的左、右顶点分别为 、 ，点 是椭圆上异于 、 的任意一点， 设直线 、 的斜率分别为 、 ，证明 为定值； //MN CDEF MN AH⊥ CDEFA − C x 3 3e = : 2l y x= + C O C C 1A 2A M 1A 2A 1MA 2MA 1k 2k 1 2k k⋅ A B D C E N M F (其中 , ,H M N 分别是 DE, BCAF, 中点) 正视图 22 2 2 2 2 2 2 侧视图 俯视图 H 20、（本题满分 13 分）已知 成等差数列．又数列 此数列的前 n 项 的和 （ ）对所有大于 1 的正整数 n 都有 ． （1）求数列 的通项； （2）若 的等比中项，求数列 的前 n 项和 。 21、（本题满分 13 分）定义函数 （1）求 的极值点；（2）求证： 。 2013 届高考数学（文）一轮复习第十次测试参考答案 一、选择题： 1．（C） 2．（B） 3．（C） 4．（D） 5．（C） 6．（D） 7．（A） 8．（C） 9．(C) 10．（A） )0(3,2 )(, ≥xxfx ,3,)0}({ 1 => aaa nn 中 +∈ Nn )( 1−= nn SfS }{ na nn n aab 1,1 1+ 是 ( ) (1 ) 1, 2,n nf x x x n N= + − > − ∈ 3 ( )f x ( )nf x nx≥ nS }{ nb nT 二、填空题：11. 12. 13. 14. 15. 153 三、解答题： 16.解：（1） 令 ，递增区间为 （2）由 即 ，故 ，解得 ， 又由于 所以 ， 故 17．解：（1）由茎叶图可知：甲班的成绩的中位数是 113 乙班的成绩分别是：107，109，109，113，114，118，120，122，127，128 （2）设事件 A：“优秀成绩”中，被抽取的甲班学生成绩高于乙班 甲班的“优秀成绩”有 4 个：121，121，128，122 乙班的“优秀成绩”有 4 个：120，122，127，128 按题意抽取后，比较成绩高低的情况列举如下 121 121 128 122 120 121>120 甲 高 121>120 甲 高 128>120 甲 高 122>120 甲 高 122 121<122 乙 高 121<122 乙 高 128>122 甲 高 122=122 乙 高 127 121<127 乙 高 121<127 乙 高 128>127 甲 高 122<127 乙 高 128 121<128 乙 高 121<128 乙 高 128=128 乙 高 122<128 乙 高 由表格可知 18.解：由三视图知,该多面体是底面为等腰直角三角形的直三棱柱，侧面 ABCD 和侧面 ABFE 为边长为 2 的正方形 （1） 正方形 ABEF，∴连接 BE，则 BE 与 AF 交于中点 M，∴连接 EC ， 中， 分别是 中点 故中位线 ， 而 面 ， 面 ∴ 面 (2) 为等腰直角三角形，且 H 为中点 ∴ ① 该多面体是直三棱柱，故侧棱 面 ，而 面 ，故 ② 综合①②,且 面 ∴ 面 ， 而 面 ∴ 由（1）可知， ， ∴ （3）由（1）可知 面 , 为高，且 ∴ 19．解：（Ⅰ） 直线 与以原点为圆心，椭圆 的短半轴为半径的圆 相切． 2 0x y− = )24,7(− 2 3+ ( ) 2sin cos cos2 sin2 cos2 2 sin(2 )4f x x x x x x x π= − = − = − πππππ kxk 224222 +≤−≤+− ⇒ ππππ kxk +≤≤+− 8 3 8 3[ , ]8 8k k k Z π ππ π− + + ∈ 1)( =Af 1)42sin(2 =− π A 2 2)42sin( =− π A 2 24 4A k π ππ∴ − = + 4A k ππ= + 20 π<< A 4A π= 224sin82 1sin2 1 =××== π AbcS 107+109+109+113+114+118+120 122+127+128 116.710x += =乙 6 3( ) 16 8P A = =  BEC∆ NM , ,BE BC / /MN EC MN ⊄ CDEF EC ⊂ CDEF //MN CDEF  ABE∆ DEAH ⊥  EF ⊥ ABE AH ⊂ ABE AH EF⊥ , ,DE EF E DE EF∩ = ⊂ DCFE AH ⊥ DCFE EC ⊂ CDEF AH ⊥ EC / /MN EC AH ⊥ MN ⊥AH DCEF AH 2=AH 3 822223 1 3 1 =×××=⋅=− AHSV CDEFCDEFA  : 2l y x= + C O 2 2 ∴ ∴ 又由 ，解得 椭圆方程 （Ⅱ）证明：由椭圆方程得 ， 设 点坐标 ，则 ， 是定值 20. 解：（1） 成等差数列 即 所以 为等差数列，首项 ，公差 ，故 时， 时， 经检验， 亦满足，故 （2） 的等比中项， 21. （1） ，令 ， 定义域 - 0 + 为极小值点，无极大值点。 （2）证明： 令 ，则 。 令 得 当 时， ， 为奇数时， ； 为偶数时， ； 当 时， ， 时， ，故 <0，函数 单调递减； 而 ， ，故 >0，函数 单调递增； ∴ 在 x＝0 处取得最小值 。∴ ，即 （当且仅当 x＝0 时取等号）。 2 2 0 0 2 2 1 1 d b − += = = + 2 2 2 2b a c= − = 3 3 ce a = = 3, 1a c= = 2 2 13 2 x y+ = 1( 3,0)A − 2 ( 3,0)A M ( , )o ox y 2 2 2 221 (3 )3 2 3 o o o o x y y x+ = ⇒ = − 1 3 o MA o yk x = + 2 3 o MA o yk x = − 1 2 2 2 2 2 2 (3 ) 23 3 3 3 o o MA MA o o xyk k x x − ⋅ = = = −− − ∴ 1 2MA MAk k⋅  )0(3,2 )(, ≥xxfx 2( ) 3 ( ) ( 3)f x x f x x∴ = + ∴ = +  )( 1−= nn SfS 2 1( 3)n nS S −∴ = + 1 3n nS S −− = { }nS 1 3S = 3 3 3( 1) 3nS n n= + − = 23nS n= 1n = 1 1 3a S= = 2n ≥ 2 2 1 3 3( 1) 6 3n n na S S n n n−= − = − − = − 1 3a = 6 3na n n N= − ∈ nn n aab 1,1 1+ 是 1 1 1 (6 3)(6 3)n n n b a a n n+ ∴ = = + − 1 1 1 1( )9(2 1)(2 1) 18 2 1 2n 1n n n = = −+ − − + 1 2 1 1 1 1 1 1 1 1 1[( ) ( ) ( )] (1 )18 1 3 3 5 2 1 2 1 18 2 1n nT b b b n n n ∴ = + + = − + − + − = −− + +  3 3 ( ) (1 ) 1f x x= + − 2 3 ( ) 3(1 )f x x′ = + 3 ( ) 0f x′ = 1x = − ( 2, )− +∞ x ( 2, 1)− − 1− ( 1, )− +∞ ( )f x′ 1x∴ = − ( ) (1 ) 1n nf x nx x nx− = + − − ( ) (1 ) 1ng x x nx= + − − ( ) ( ) 11 1ng x n x − ′ = + −  ( ) 0g x′ = 0x = ( 2, 1)x∈ − − 1 1 0x− < + < n (1 ) 0 1nx+ < < n 0 (1 ) 1nx< + < [ 1,0)x∈ − 0 1 1x≤ + < 0 (1 ) 1nx< + < ( 2,0)x∴ ∈ − (1 ) 1nx+ < ( ) ( ) 11 1ng x n x − ′ = + −  ( )g x ( )0,x∈ ∞ (1 ) 1nx+ > ( ) ( ) 11 1ng x n x − ′ = + −  ( )g x ( )g x (0) 0g = ( ) 0g x ≥ ( )nf x nx≥