高考数学总复习
2011年高考数学总复习
一、 函数
1、 若集合A中有n个元素,则集合A的所有不同的子集个数为,所有非空真子集的个数是。
二次函数的图象的对称轴方程是,顶点坐标是。用待定系数法求二次函数的解析式时,解析式的设法有三种形式,即,和 (顶点式)。
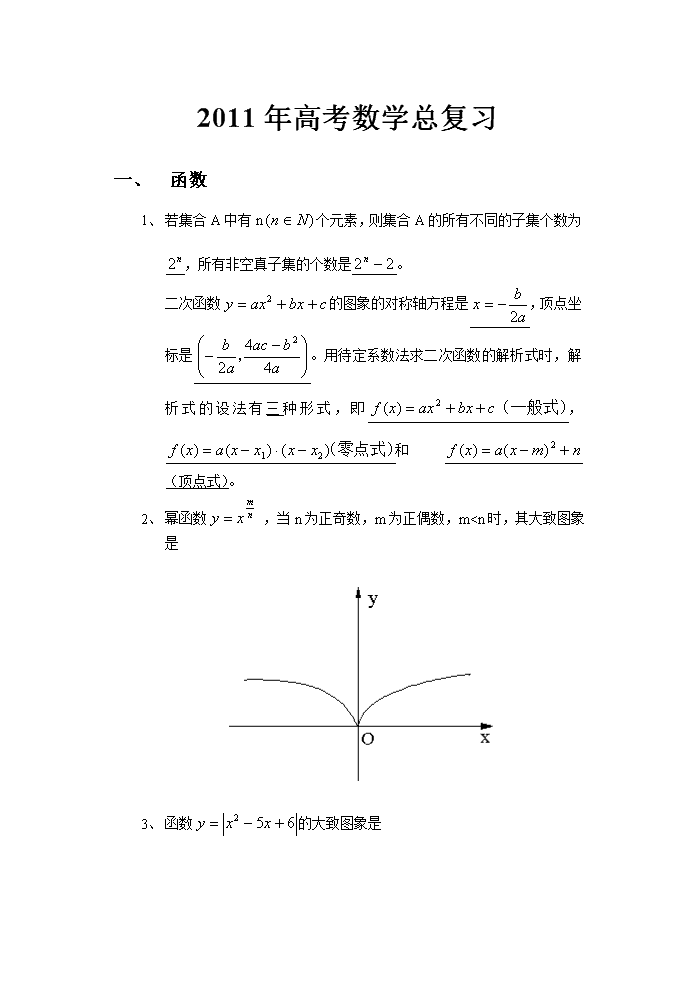
2、 幂函数 ,当n为正奇数,m为正偶数,m
0,=0,<0,等价于直线与圆相交、相切、相离;
②考查圆心到直线的距离与半径的大小关系:距离大于半径、等于半径、小于半径,等价于直线与圆相离、相切、相交。
15、抛物线标准方程的四种形式是:
16、抛物线的焦点坐标是:,准线方程是:。
若点是抛物线上一点,则该点到抛物线的焦点的距离(称为焦半径)是:,过该抛物线的焦点且垂直于抛物线对称轴的弦(称为通径)的长是:。
17、椭圆标准方程的两种形式是:和
。
18、椭圆的焦点坐标是,准线方程是,离心率是,通径的长是。其中。
19、若点是椭圆上一点,是其左、右焦点,则点P的焦半径的长是和
。
20、双曲线标准方程的两种形式是:和
。
21、双曲线的焦点坐标是,准线方程是,离心率是,通径的长是,渐近线方程是。其中。
22、与双曲线共渐近线的双曲线系方程是。与双曲线共焦点的双曲线系方程是。
23、若直线与圆锥曲线交于两点A(x1,y1),B(x2,y2),则弦长为 ;
若直线与圆锥曲线交于两点A(x1,y1),B(x2,y2),则弦长为 。
24、圆锥曲线的焦参数p的几何意义是焦点到准线的距离,对于椭圆和双曲线都有:。
25、平移坐标轴,使新坐标系的原点
在原坐标系下的坐标是(h,k),若点P在原坐标系下的坐标是在新坐标系下的坐标是,则=,=。
一、 极坐标、参数方程
1、 经过点的直线参数方程的一般形式是:。
2、 若直线经过点,则直线参数方程的标准形式是:。其中点P对应的参数t的几何意义是:有向线段的数量。
若点P1、P2、P是直线上的点,它们在上述参数方程中对应的参数分别是则:;当点P分有向线段时,;当点P是线段P1P2的中点时,。
3、圆心在点,半径为的圆的参数方程是:。
3、 若以直角坐标系的原点为极点,x轴正半轴为极轴建立极坐标系,点P的极坐标为直角坐标为,则,,。
1、 经过极点,倾斜角为的直线的极坐标方程是:,
经过点,且垂直于极轴的直线的极坐标方程是:,
经过点且平行于极轴的直线的极坐标方程是:,
经过点且倾斜角为的直线的极坐标方程是:。
2、 圆心在极点,半径为r的圆的极坐标方程是;
圆心在点的圆的极坐标方程是;
圆心在点的圆的极坐标方程是;
圆心在点,半径为的圆的极坐标方程是。
3、 若点M、N,则。
二、 立体几何
1、求二面角的射影公式是,其中各个符号的含义是:是二面角的一个面内图形F的面积,是图形F在二面角的另一个面内的射影,是二面角的大小。
2、若直线在平面内的射影是直线,直线m是平面内经过的斜足的一条直线,与所成的角为,与m所成的角为, 与m所成的角为θ,则这三个角之间的关系是。
3、体积公式:
柱体:,圆柱体:。
斜棱柱体积:(其中,是直截面面积,是侧棱长);
锥体:,圆锥体:。
台体:, 圆台体:
球体:。
3、 侧面积:
直棱柱侧面积:,斜棱柱侧面积:;
正棱锥侧面积:,正棱台侧面积:;
圆柱侧面积:,圆锥侧面积:,
圆台侧面积:,球的表面积:。
5、几个基本公式:
弧长公式:(是圆心角的弧度数,>0);
扇形面积公式:;
圆锥侧面展开图(扇形)的圆心角公式:;
圆台侧面展开图(扇环)的圆心角公式:。
经过圆锥顶点的最大截面的面积为(圆锥的母线长为,轴截面顶角是θ):
十一、比例的几个性质
1、比例基本性质:
2、反比定理:
3、更比定理:
3、 合比定理;
4、 分比定理:
5、 合分比定理:
6、 分合比定理:
7、 等比定理:若,,则。
十二、复合二次根式的化简
当是一个完全平方数时,对形如的根式使用上述公式化简比较方便。