高考理科数学试题及答案

高考理科数学试题及答案

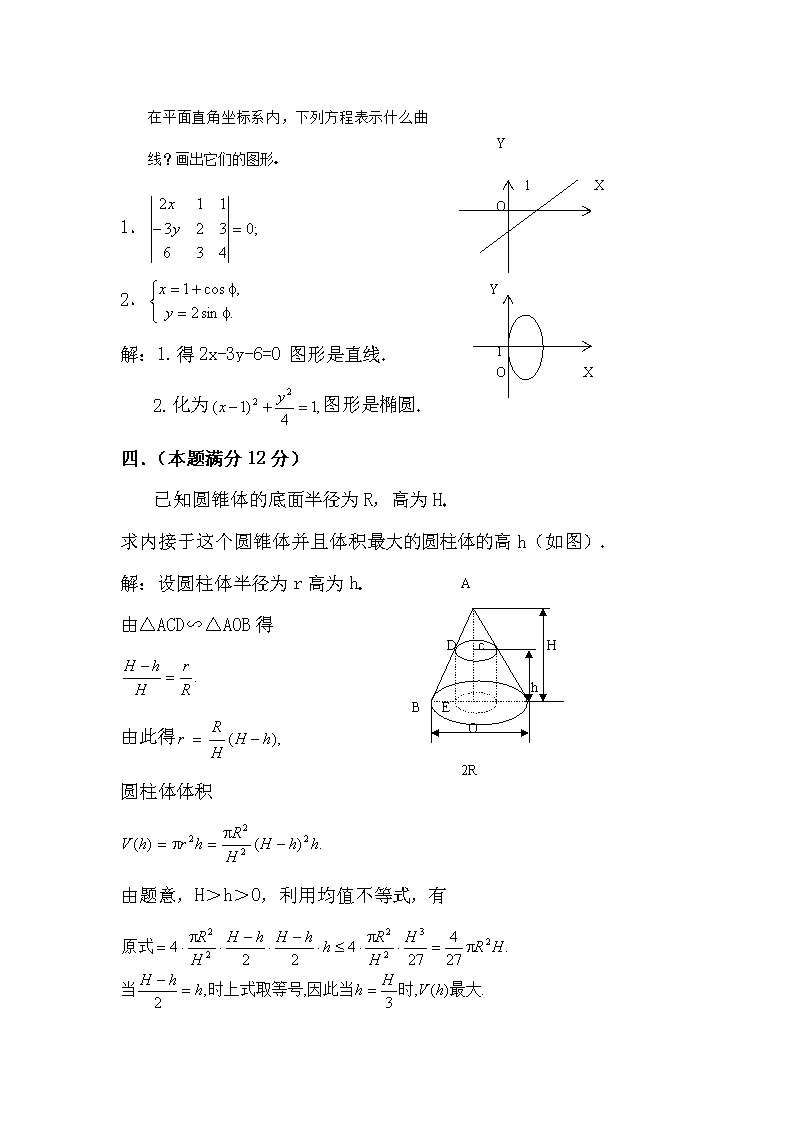
‎1982年普通高等学校招生全国统一考试 数学（理科）‎ 一．（本题满分6分）‎ 填表：‎ 函 数 使函数有意义的x的实数范围 ‎1‎ ‎{0}‎ ‎2‎ R ‎3‎ R ‎4‎ ‎[-1,1]‎ ‎5‎ ‎(0,+∞）‎ ‎6‎ R 解：见上表 二．（本题满分9分）‎ ‎1．求（-1+i)20展开式中第15项的数值;‎ ‎2．求的导数 解：1.第15项T15=‎ ‎2.‎ 三．（本题满分9分）‎ ‎ Y ‎ ‎ ‎ ‎ 1 X ‎ ‎ O ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ Y ‎ ‎ ‎ ‎ ‎ ‎ 1 ‎ ‎ O X ‎ 在平面直角坐标系内，下列方程表示什么曲线？画出它们的图形 ‎1．‎ ‎2．‎ 解：1.得2x-3y-6=0图形是直线 ‎2.化为图形是椭圆 四．（本题满分12分）‎ 已知圆锥体的底面半径为R，高为H 求内接于这个圆锥体并且体积最大的圆柱体的高h（如图）‎ ‎ A ‎ ‎ ‎ ‎ ‎ ‎ D c H ‎ ‎ ‎ ‎ h ‎ B E ‎ ‎ O ‎ ‎ ‎ ‎ 2R ‎ 解：设圆柱体半径为r高为h 由△ACD∽△AOB得 由此得 圆柱体体积 由题意，H＞h＞0，利用均值不等式，有 ‎（注：原“解一”对h求导由驻点解得）‎ 五．（本题满分15分）‎ ‎（要写出比较过程）‎ 解一：当>1时，‎ 解二：‎ 六．（本题满分16分）‎ ‎ A ‎ ‎ ‎ ‎ M P（ρ，θ） ‎ ‎ X ‎ ‎ ‎ ‎ O ‎ ‎ N B ‎ 如图：已知锐角∠AOB=2α内有动点P，PM⊥OA，PN⊥OB，且四边形PMON的面积等于常数c2今以O为极点，∠AOB的角平分线OX为极轴，求动点P的轨迹的极坐标方程，并说明它表示什么曲线 解：设P的极点坐标为（ρ，θ）∴∠POM=α-θ，∠NOM=α+θ，‎ OM=ρcos(α-θ),PM=ρsin(α-θ),‎ ON=ρcos(α+θ),PN=ρsin(α+θ),‎ 四边形PMON的面积 这个方程表示双曲线由题意，‎ 动点P的轨迹是双曲线右面一支在∠AOB内的一部分 七．（本题满分16分）‎ 已知空间四边形ABCD中AB=BC，CD=DA，M，N，P，Q分别是边AB，BC，CD，DA的中点（如图）求证MNPQ是一个矩形 ‎ B ‎ ‎ ‎ ‎ M ‎ ‎ R ‎ ‎ A N ‎ ‎ Q D ‎ ‎ K S ‎ ‎ P ‎ ‎ C ‎ 证：连结AC，在△ABC中，‎ ‎∵AM=MB，CN=NB，∴MN∥AC 在△ADC中，∵AQ=QD，CP=PD，‎ ‎∴QP∥AC∴MN∥QP 同理，连结BD可证MQ∥NP ‎∴MNPQ是平行四边形 取AC的中点K，连BK，DK ‎∵AB=BC，∴BK⊥AC，‎ ‎∵AD=DC，∴DK⊥AC因此平面BKD与AC垂直 ‎∵BD在平面BKD内，∴BD⊥AC∵MQ∥BD，QP∥AC，∴MQ⊥QP，即∠MQP为直角故MNPQ是矩形 八．（本题满分18分）‎ ‎ Y ‎ ‎ x2=2qy ‎ ‎ ‎ ‎ y2=2px ‎ ‎ A1 ‎ ‎ ‎ ‎ O A‎2 A3 X ‎ 抛物线y2=2px的内接三角形有两边与抛物线x2=2qy相切，证明这个三角形的第三边也与x2=2qy相切 解：不失一般性，设p>0,q>0.又设y2=2px的内接三角形顶点为 A1（x1,y1),A2(x2,y2),A3(x3,y3)‎ 因此y12=2px1，y22=2px2 ，y32=2px3‎ 其中y1≠y2 , y2≠y3 , y3≠y1 .‎ 依题意，设A‎1A2，A‎2A3与抛物线x2=2qy相切，要证A‎3A1也与抛物线x2=2qy相切 因为x2=2qy在原点O处的切线是y2=2px的对称轴，所以原点O不能是所设内接三角形的顶点即（x1,y1),(x2,y2),(x3,y3)，都不能是（0，0）;又因A‎1A2与x2=2qy相切，所以A‎1A2不能与Y轴平行，即x1≠x2 , y1≠-y2,直线A‎1A2的方程是 同理由于A‎2A3与抛物线x2=2qy相切，A‎2A3也不能与Y轴平行，即 x2≠x3, y2≠-y3,同样得到 由（1）（2）两方程及y2≠0,y1≠y3,得y1+y2+y3=0.‎ 由上式及y2≠0,得y3≠-y1，也就是A‎3A1也不能与Y轴平行今将y2=-y1-y3代入（1）式得：‎ ‎(3)式说明A‎3A1与抛物线x2=2qy的两个交点重合，即A‎3A1与抛物线x2=2qy相切所以只要A‎1A2，A‎2A3与抛物线x2=2qy相切，则A‎3A1也与抛物线x2=2qy相切 九．（附加题，本题满分20分，计入总分）‎ 已知数列和数列其中 ‎1．用p,q,r,n表示bn，并用数学归纳法加以证明;‎ ‎2．求 解：1.∵1=p, n=pn-1,∴n=pn.‎ 又b1=q,‎ ‎ b2=q1+rb1=q(p+r),‎ ‎ b3=q2+rb2=q(p2+pq+r2),…‎ 设想 用数学归纳法证明：‎ 当n=2时，等式成立; ‎ 设当n=k时，等式成立，即 则bk+1=qk+rbk=‎ 即n=k+1时等式也成立 所以对于一切自然数n≥2，都成立