贵州高考数学试卷全国大纲卷

贵州高考数学试卷全国大纲卷

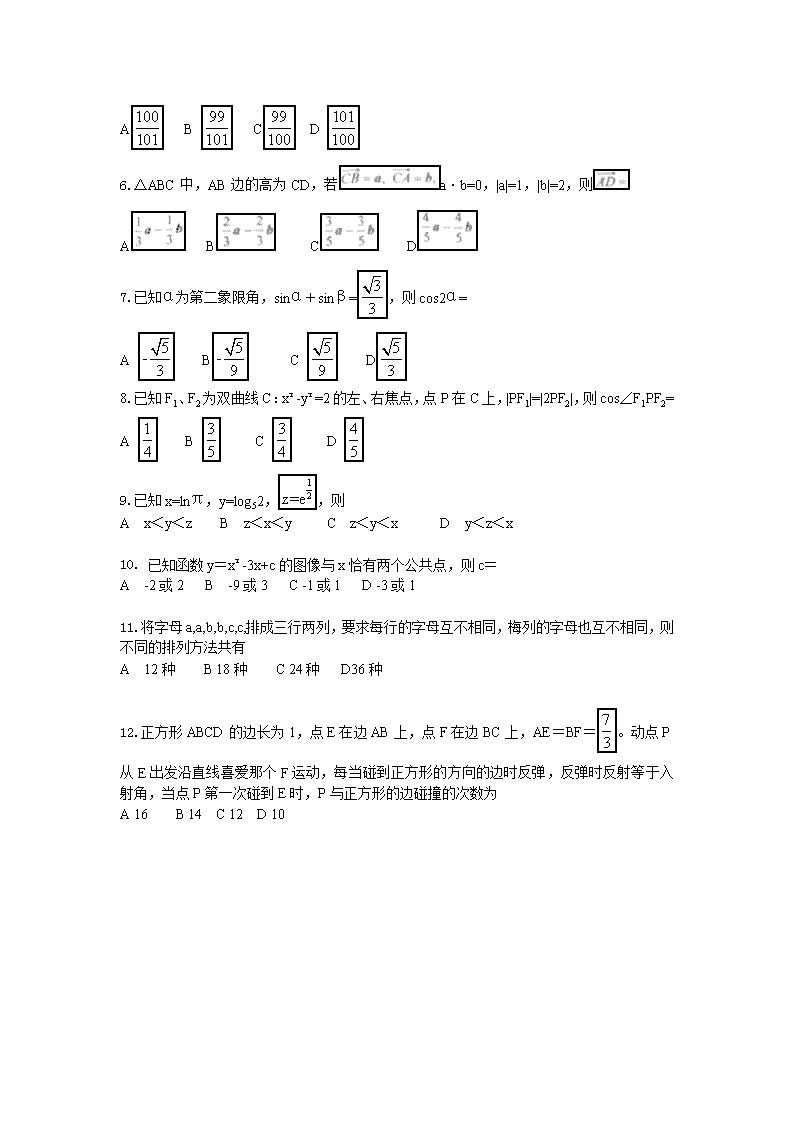
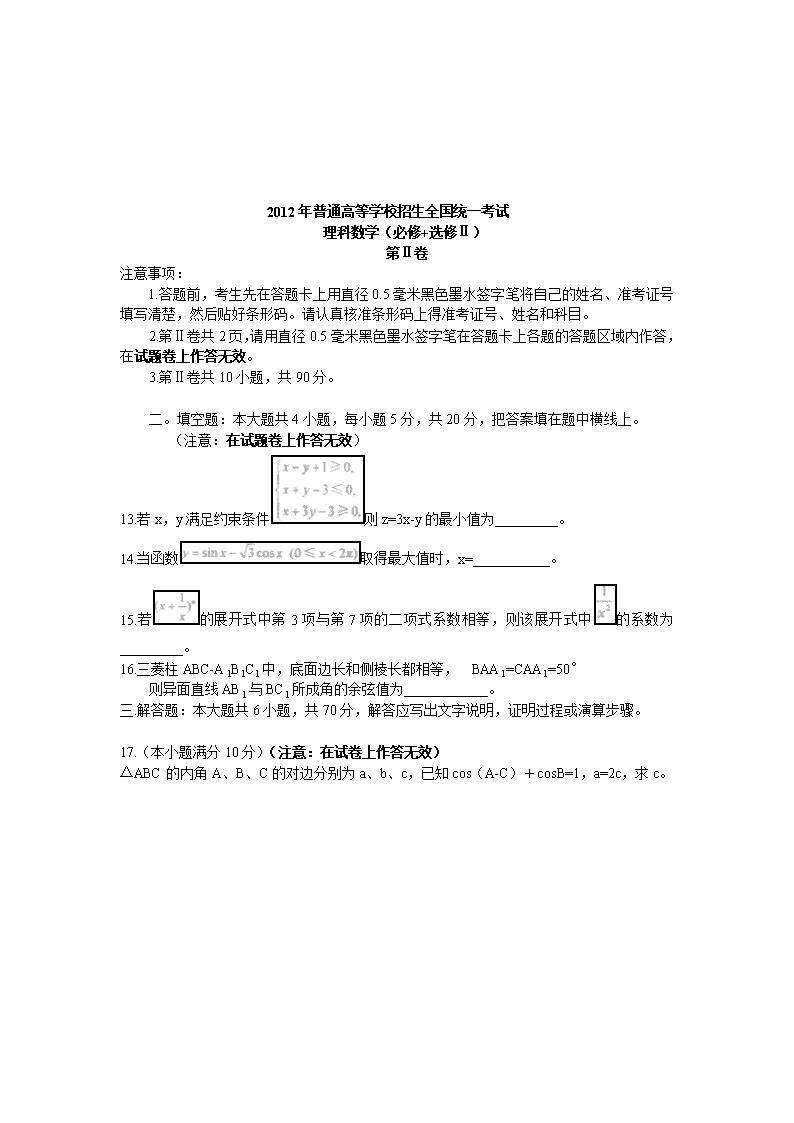
‎2012年普通高等学校招生全国统一考试 理科数学（必修+选修II）‎ 本试卷分第I卷（选择题）和第II卷（非选择题）两部分，第I卷第1至2页，第II卷第3至第4页。考试结束，务必将试卷和答题卡一并上交。‎ 第I卷 注意事项：‎ 全卷满分150分，考试时间120分钟。‎ 考生注意事项：‎ ‎1.答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。请认真核准该条形码上的准考证号、姓名和科目。‎ ‎2.没小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。在试题卷上作答无效。‎ ‎3.第I卷共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ 一、 选择题 1． 复数=‎ A 2+i B 2-i C 1+2i D 1- 2i ‎ ‎2．已知集合A＝{1.3. }，B＝{1，m} ,AB＝A, 则m=‎ A 0或 B 0或‎3 ‎‎ C 1或 D 1或3 ‎ ‎3．椭圆的中心在原点，焦距为4 一条准线为x=-4 ，则该椭圆的方程为 A +=1 B +=1‎ C +=1 D +=1‎ ‎4．已知正四棱柱ABCD- A1B‎1C1D1中 ，AB=2，CC1= E为CC1的中点，则直线AC1与平面BED的距离为 A 2 B C D 1‎ ‎5.已知等差数列{an}的前n项和为Sn，a5=5，S5=15，则数列的前100项和为 A B C D ‎ ‎6.△ABC中，AB边的高为CD，若a·b=0，|a|=1，|b|=2，则 A B C D ‎7.已知α为第二象限角，sinα＋sinβ=，则cos2α=‎ A B C D ‎8.已知F1、F2为双曲线C：x²-y²=2的左、右焦点，点P在C上，|PF1|=|2PF2|，则cos∠F1PF2=‎ A B C D ‎ ‎9.已知x=lnπ，y=log52，，则 A x＜y＜z B z＜x＜y C z＜y＜x D y＜z＜x ‎10. 已知函数y＝x²-3x+c的图像与x恰有两个公共点，则c＝‎ A -2或2 B -9或3 C -1或1 D -3或1‎ ‎11.将字母a,a,b,b,c,c,排成三行两列，要求每行的字母互不相同，梅列的字母也互不相同，则不同的排列方法共有 A 12种 B 18种 C 24种 D36种 ‎12.正方形ABCD的边长为1，点E在边AB上，点F在边BC上，AE＝BF＝。动点P从E出发沿直线喜爱那个F运动，每当碰到正方形的方向的边时反弹，反弹时反射等于入射角，当点P第一次碰到E时，P与正方形的边碰撞的次数为 A 16 B 14 C 12 D 10‎ ‎ ‎ ‎ 2012年普通高等学校招生全国统一考试 ‎ 理科数学（必修+选修Ⅱ）‎ ‎ 第Ⅱ卷 注意事项：‎ ‎ 1.答题前，考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，然后贴好条形码。请认真核准条形码上得准考证号、姓名和科目。‎ ‎2.第Ⅱ卷共2页，请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，在试题卷上作答无效。‎ ‎3.第Ⅱ卷共10小题，共90分。‎ 二。填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上。‎ ‎ （注意：在试题卷上作答无效）‎ ‎13.若x，y满足约束条件则z=3x-y的最小值为_________。‎ ‎14.当函数取得最大值时，x=___________。‎ ‎15.若的展开式中第3项与第7项的二项式系数相等，则该展开式中的系数为_________。‎ ‎16.三菱柱ABC-A1B‎1C1中，底面边长和侧棱长都相等， BAA1=CAA1=50°‎ 则异面直线AB1与BC1所成角的余弦值为____________。‎ 三.解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤。‎ ‎17.（本小题满分10分）（注意：在试卷上作答无效）‎ ‎△ABC的内角A、B、C的对边分别为a、b、c，已知cos（A-C）＋cosB=1，a=‎2c，求c。‎ ‎18.（本小题满分12分）（注意：在试题卷上作答无效）‎ 如图，四棱锥P-ABCD中，底面ABCD为菱形，PA⊥底面ABCD，AC=2，PA=2，E是PC上的一点，PE=2EC.‎ ‎（Ⅰ）证明：PC⊥平面BED；‎ ‎（Ⅱ）设二面角A-PB-C为90°，求PD与平面PBC所成角的大小。‎ ‎19. （本小题满分12分）（注意：在试题卷上作答无效）‎ 乒乓球比赛规则规定：一局比赛，双方比分在10平前，一方连续发球2次后，对方再连续发球2次，依次轮换。每次发球，胜方得1分，负方得0分。设在甲、乙的比赛中，每次发球，发球方得1分的概率为0.6，各次发球的胜负结果相互独立。甲、乙的一局比赛中，甲先发球。‎ ‎（Ⅰ）求开始第4次发球时，甲、乙的比分为1比2的概率；‎ ‎（Ⅱ）表示开始第4次发球时乙的得分，求的期望。‎ ‎20.（本小题满分12分）（注意：在试题卷上作答无效）‎ 设函数f（x）=ax+cosx，x∈[0，π]。‎ ‎（Ⅰ）讨论f（x）的单调性；‎ ‎（Ⅱ）设f（x）≤1+sinx，求a的取值范围。‎ ‎21.（本小题满分12分）（注意：在试卷上作答无效）‎ 已知抛物线C：y=(x+1)2与圆M：（x-1）2+()2=r2(r＞0)有一个公共点，且在A处两曲线的切线为同一直线l.‎ ‎（Ⅰ）求r；‎ ‎（Ⅱ）设m、n是异于l且与C及M都相切的两条直线，m、n的交点为D，求D到l的距离。‎ ‎22.（本小题满分12分）（注意：在试卷上作答无效）‎ 函数f(x)=x2-2x-3，定义数列{xn}如下：x1=2，xn+1是过两点P（4,5）、Qn(xn,f(xn))的直线PQn与x轴交点的横坐标。‎ ‎（Ⅰ）证明：2 xn＜xn+1＜3；‎ ‎（Ⅱ）求数列{xn}的通项公式。‎