高考数学复习导数练习题

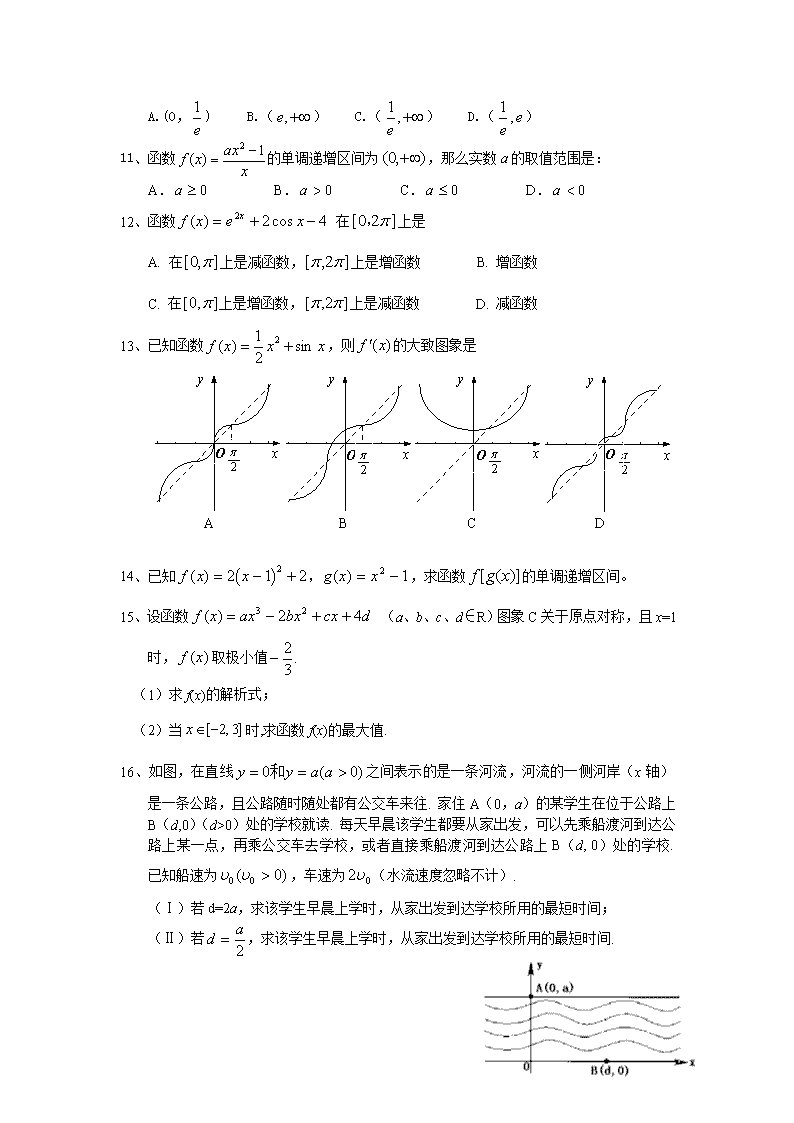
高考数学复习导数练习题

高考数学复习导数练习题 考试要求：1、了解导数概念的某些实际背景（如瞬时速度、加速度、光滑曲线切线的斜率等）；掌握函数一点处的导数的定义和导数的几何意义；理解导函数的概念。2、熟记基本导数公式((m为有理数) 的导数)；掌握两个函数和、差、积、商的求导法则。了解复合函数的求导法则，会求某些简单函数的导数。3、理解可导函数的单调性与其导数的关系；了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号)；会求一些实际问题的最大值和最小值。‎ ‎1、曲线在处的切线的倾斜角是:‎ ‎ A． B． C． D．‎ ‎2、已知物体的运动方程是（表示时间，表示位移），则瞬时速度为 ‎ 0的时刻是：‎ ‎ A．0秒、2秒或4秒 B．0秒、2秒或16秒 ‎ C．2秒、8秒或16秒 D．0秒、4秒或8秒 ‎3、设曲线和曲线在它们交点处的两切线的夹角为θ，则 A．1 B． C． D． ‎4、已知，则等于（ ）‎ ‎ A. 0 B. C. D. 2‎ ‎5、函数，若，则，，的大小关系为：‎ A． B． ‎ C． D． ‎ ‎6、设是可导函数，且 ‎ ‎ A． B．－‎1 ‎C．0 D．－2‎ ‎7、已知直线切于点（1，3），则b的值为：‎ ‎ A．3 B．－‎3 ‎C．5 D．－5‎ ‎8、函数的极值是_________．‎ ‎9、函数的单调减区间是 。‎ ‎10、函数的单调递增区间为：‎ A.(0，) B.（） C.（） D.（）‎ ‎11、函数的单调递增区间为，那么实数a的取值范围是：‎ ‎ A． B． C． D．‎ ‎12、函数 在上是 A. 在上是减函数，上是增函数 B. 增函数 ‎ C. 在上是增函数，上是减函数 D. 减函数 ‎13、已知函数，则的大致图象是 O y x y x y O x O x y O A B C D ‎14、已知，求函数的单调递增区间。‎ ‎15、设函数 （a、b、c、d∈R）图象C关于原点对称，且x=1时，取极小值 ‎（1）求f(x)的解析式；‎ ‎（2）当时,求函数f(x)的最大值.‎ ‎16、如图，在直线之间表示的是一条河流，河流的一侧河岸（x轴）是一条公路，且公路随时随处都有公交车来往. 家住A（0，a）的某学生在位于公路上B（d,0）（d>0）处的学校就读. 每天早晨该学生都要从家出发，可以先乘船渡河到达公路上某一点，再乘公交车去学校，或者直接乘船渡河到达公路上B（d, 0）处的学校. 已知船速为，车速为（水流速度忽略不计）.‎ ‎ （Ⅰ）若d=‎2a，求该学生早晨上学时，从家出发到达学校所用的最短时间；‎ ‎ （Ⅱ）若，求该学生早晨上学时，从家出发到达学校所用的最短时间.‎ ‎17、已知函数在上是增函数，。当时，函数的最大值与最小值的差为，试求的值。‎ ‎18、已知函数 ‎（1）求在函数图象上点A处的切线的方程；‎ ‎（2）若切线与y轴上的纵截距记为，讨论的单调增区间。‎ 十三、导数参考答案 ‎1、B；2、D；3、C；4、B；5、A；6、B；7、A；8、-26；9、；10、C ‎11、A；12、B；13、B.‎ ‎14. 解：设 ‎ 则，令 ‎ ‎ 解得：，或，由于是R上的连续函数，所以函数的单调递增区间为和 ‎15、解． （1）∵函数图象关于原点对称，∴对任意实数，，即恒成立 ‎ ，‎ 时，取极小值，‎ 解得 ‎ ‎(2) 令得 x ‎1‎ ‎+‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ ‎↑‎ 极大值 ‎↓‎ 极小值－‎ ‎↑‎ 又, ，故当时,. ‎ ‎16、解：（I）设该学生从家出发，先乘船渡河到达公路上某一点P(x,0) (0≤x≤d)，再乘公交车去学校，所用的时间为t，则. ‎ ‎ 令 ‎ 且当 ‎ 当 ‎ ‎ 当时，所用的时间最短，最短时间为：‎ ‎. ‎ 答：当d=‎2a时，该学生从家出发到达学校所用的最短时间是.‎ ‎（II）由（I）的讨论可知，当d=上的减函数，所以当时，‎ 即该学生直接乘船渡河到达公路上学校，所用的时间最短 最短的时间为 答：当时，该学生从家出发到达学校所用的最短时间是.‎ ‎17、解： ，在上是增函数 在上恒成立 ，恒成立 ‎ ，‎ 设则 当时， ‎ ‎ ‎ 当时，‎ 不符题意 综上，的取值为 ‎ ‎18、（1），切线的方程：‎ ‎（2）令x=0，‎ ① 当a>0时,由，‎ ②当a=0时,由 ③当a<0时, ‎ 综合①②③当 ‎ 当a=0时, ‎ 当a<0时, ‎