高考数学第九章平面解析几何第9课时抛物线更多资料关注微博高中学习资料库

高考数学第九章平面解析几何第9课时抛物线更多资料关注微博高中学习资料库

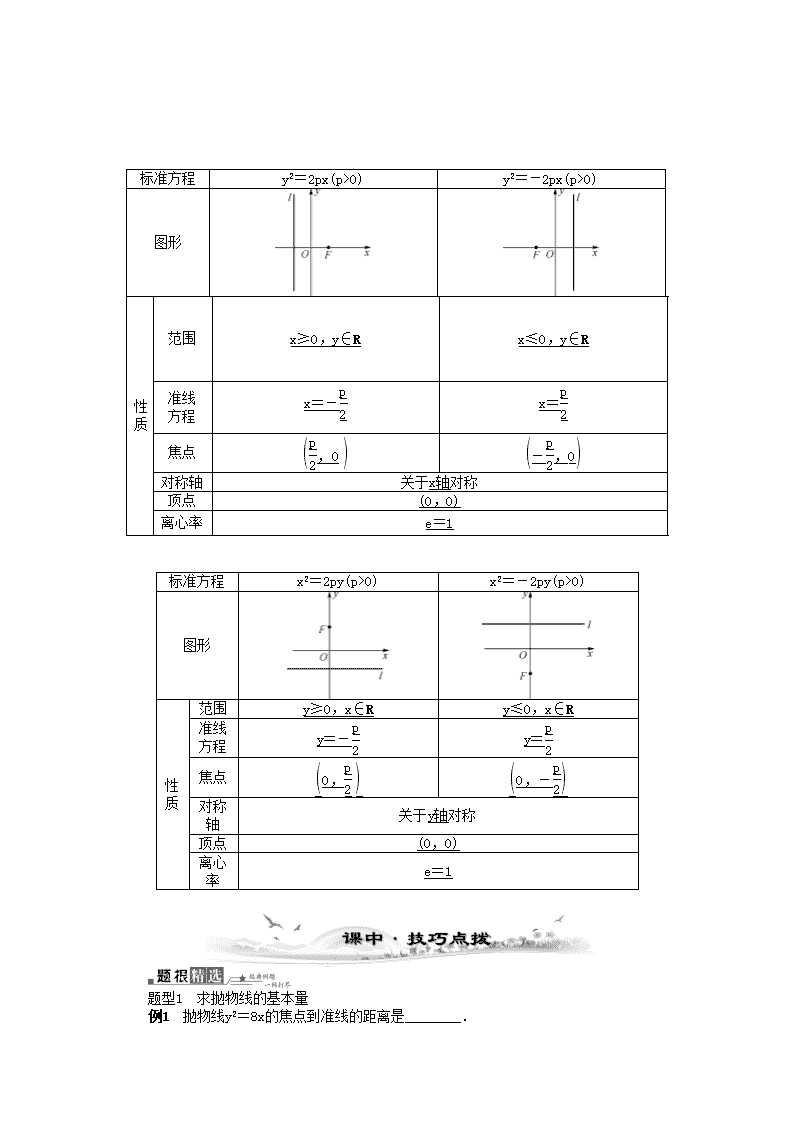
第九章 平面解析几何第9课时　抛 物 线 考情分析 考点新知 建立并掌握抛物线的标准方程，能根据已知条件求抛物线的标准方程；掌握抛物线的简单几何性质，能运用抛物线的几何性质处理一些简单的实际问题．‎ ‎① 了解抛物线的定义、几何图形和标准方程，了解它们的简单几何性质.‎ ‎②掌握抛物线的简单应用.‎ ‎1. 已知抛物线的焦点坐标是(0，－3)，则抛物线的标准方程是________．‎ 答案：x2＝－12y 解析：∵ ＝3，∴ p＝6，∴ x2＝－12y.‎ ‎2. 抛物线y2＝－8x的准线方程是________．‎ 答案：x＝2‎ 解析：∵ 2p＝8，‎ ‎∴ p＝4，故所求准线方程为x＝2.‎ ‎3. 抛物线y＝ax2的准线方程是y＝2，则a的值是________．‎ 答案：－ 解析：抛物线的标准方程为x2＝y.则a＜0且2＝－，得a＝－.‎ ‎4. (选修11P44习题2改编)抛物线y2＝4x上一点M到焦点的距离为3，则点M的横坐标x＝________．‎ 答案：2‎ 解析：∵ 2p＝4，∴ p＝2，准线方程x＝－1.由抛物线定义可知，点M到准线的距离为3，则x＋1＝3，即x＝2.‎ ‎5. 已知斜率为2的直线l过抛物线y2＝ax(a＞0)的焦点F，且与y轴相交于点A，若△OAF(O为坐标原点)的面积为4，则抛物线方程为________．‎ 答案：y2＝8x 解析：依题意得，OF＝，又直线l的斜率为2，可知AO＝2OF＝，△AOF的面积等于·AO·OF＝＝4，则a2＝64.又a＞0，所以a＝8，该抛物线的方程是y2＝8x.‎ ‎1. 抛物线的定义 平面内到一个定点F和一条定直线l(F不在l上)距离相等_的点的轨迹叫做抛物线，点F叫做抛物线的焦点，直线l叫做抛物线的准线．‎ ‎2. 抛物线的标准方程和几何性质(如下表所示)‎ 标准方程 y2＝2px(p>0)‎ y2＝－2px(p>0)‎ 图形 性质 范围 x≥0，y∈R x≤0，y∈R 准线 方程 x＝－ x＝ 焦点 对称轴 关于x轴对称 顶点 ‎(0，0)‎ 离心率 e＝1‎ 标准方程 x2＝2py(p>0)‎ x2＝－2py(p>0)‎ 图形 性质 范围 y≥0，x∈R y≤0，x∈R 准线 方程 y＝－ y＝ 焦点 对称轴 关于y轴对称 顶点 ‎(0，0)‎ 离心率 e＝1‎ 题型1　求抛物线的基本量 例1　抛物线y2＝8x的焦点到准线的距离是________．‎ 答案：4‎ 解析：由y2＝2px＝8x知p＝4，又焦点到准线的距离就是p，所以焦点到准线的距离为4.‎ 抛物线y2＝－8x的准线方程是________．‎ 答案：x＝2‎ 解析：∵2p＝8，∴p＝4，准线方程为x＝2.‎ 题型2　求抛物线的方程 例2　(选修11P44习题5改编)已知抛物线的顶点在原点，对称轴为坐标轴，焦点在直线2x－y－4＝0上，求抛物线的标准方程．‎ 解：直线2x－y－4＝0与x轴的交点是(2，0)，与y轴的交点是(0，－4)．由于抛物线的顶点在原点，对称轴为坐标轴，则①若抛物线焦点在x轴上，则抛物线的标准方程是y2＝8x；②若抛物线焦点在y轴上，则抛物线的标准方程是x2＝－16y；故所求抛物线方程为y2＝8x或x2＝－16y.‎ 已知Rt△AOB的三个顶点都在抛物线y2＝2px上，其中直角顶点O为原点，OA所在直线的方程为y＝x，△AOB的面积为6，求该抛物线的方程．‎ 解：∵ OA⊥OB，且OA所在直线的方程为y＝x，OB所在直线的方程为y＝－x，‎ 由得A点坐标为，‎ 由得B点坐标为(6p，－2p)，‎ ‎∴ OA＝|p|，OB＝4|p|，‎ 又S△OAB＝p2＝6，∴ p＝±.‎ ‎∴该抛物线的方程为y2＝3x或y2＝－3x.‎ 题型3　抛物线的几何性质探究 例3　在平面直角坐标系xOy中，抛物线C的顶点在原点，经过点A(2，2)，其焦点F在x轴上．‎ ‎(1) 求抛物线C的标准方程；‎ ‎(2) 求过点F，且与直线OA垂直的直线的方程；‎ ‎(3) 设过点M(m，0)(m>0)的直线交抛物线C于D、E两点，ME＝2DM，记D和E两点间的距离为f(m)，求f(m)关于m的表达式．‎ 解：(1)由题意，可设抛物线C的标准方程为y2＝2px.因为点A(2，2)在抛物线C上，所以p＝1.因此抛物线C的标准方程为y2＝2x.‎ ‎(2)由(1)可得焦点F的坐标是，又直线OA的斜率为＝1，故与直线OA垂直的直线的斜率为－1，因此所求直线的方程是x＋y－＝0.‎ ‎(3)(解法1)设点D和E的坐标分别为(x1，y1)和(x2，y2)，直线DE的方程是y＝k(x－m)，k≠0.‎ 将x＝＋m代入y2＝2x，有ky2－2y－‎2km＝0，解得y1，2＝.‎ 由ME＝2DM知1＋＝2(－1)，化简得k2＝.‎ 因此DE2＝(x1－x2)2＋(y1－y2)2＝(y1－y2)2＝＝(m2＋‎4m)，所以f(m)＝(m>0)．‎ ‎(解法2)设D，E.‎ 由点M(m，0)及＝2，得t2－m＝2，t－0＝2(0－s)．因此t＝－2s，m＝s2.‎ 所以f(m)＝DE＝＝(m>0)．‎ 抛物线y2＝2px的准线方程为x＝－2，该抛物线上的每个点到准线x＝－2的距离都与到定点N的距离相等，圆N是以N为圆心，同时与直线l1：y＝x和l2：y＝－x 相切的圆，‎ ‎(1) 求定点N的坐标；‎ ‎(2) 是否存在一条直线l同时满足下列条件：‎ ‎① l分别与直线l1和l2交于A、B两点，且AB中点为E(4，1)；‎ ‎② l被圆N截得的弦长为2.‎ 解：(1) 因为抛物线y2＝2px的准线方程为x＝－2.所以p＝4，根据抛物线的定义可知点N是抛物线的焦点，所以定点N的坐标为(2，0)．‎ ‎(2) 假设存在直线l满足两个条件，显然l斜率存在，设l的方程为y－1＝k(x－4)，k≠±1.以N为圆心，同时与直线l1：y＝x和l2：y＝－x 相切的圆N的半径为.因为l被圆N截得的弦长为2，所以圆心到直线的距离等于1, 即d＝＝1，解得k＝0或，当k＝0时，显然不合AB中点为E(4，1)的条件，矛盾，当k＝时，l的方程为4x－3y－13＝0.由，解得点A的坐标为(13，13)；由，解得点B的坐标为.显然AB中点不是E(4，1)，矛盾，所以不存在满足条件的直线l. ‎ ‎1. 抛物线y＝－x2上的点到直线4x＋3y－8＝0的距离的最小值是________．‎ 答案： 解析：设抛物线y＝－x2上一点为(m，－m2)，该点到直线4x＋3y－8＝0的距离为 ，当m＝时，取得最小值.‎ ‎2. 已知双曲线C1：－＝1(a>0，b>0)的离心率为2.若抛物线C2：x2＝2py(p>0)的焦点到双曲线C1的渐近线的距离为2，则抛物线C2的方程为________．‎ 答案：x2＝16y 解析：∵ 双曲线C1：－＝1(a＞0，b＞0)的离心率为2，∴＝＝2，∴ b＝a，∴双曲线的渐近线方程为x±y＝0，∴抛物线C2：x2＝2py(p＞0)的焦点到双曲线的渐近线的距离为＝2，∴ p＝8.∴ 所求的抛物线方程为x2＝16y.‎ ‎3. 已知抛物线关于x轴对称，它的顶点在坐标原点O，并且经过点M(2，y0)．若点M到该抛物线焦点的距离为3，则OM＝________．‎ 答案：2 解析：依题意，设抛物线方程是y2＝2px(p>0)，则有2＋＝3，得p＝2，故抛物线方程是y2＝4x，点M的坐标是(2，±2)，OM＝＝2.‎ ‎4. 已知抛物线D的顶点是椭圆C：＋＝1的中心，焦点与该椭圆的右焦点重合．‎ ‎(1) 求抛物线D的方程；‎ ‎(2) 过椭圆C右顶点A的直线l交抛物线D于M、N两点．‎ ‎①若直线l的斜率为1，求MN的长；‎ ‎②是否存在垂直于x轴的直线m被以MA为直径的圆E所截得的弦长为定值？如果存在，求出m的方程；如果不存在，说明理由．‎ 解：(1) 由题意，可设抛物线方程为y2＝2px(p>0)．由a2－b2＝4－3＝1，得c＝1，∴抛物线的焦点为(1，0)，∴ p＝2.‎ ‎∴抛物线D的方程为y2＝4x.‎ ‎(2) 设M(x1，y1)，N(x2，y2)．‎ ‎①直线l的方程为y＝x－4，联立整理得x2－12x＋16＝0，即M(6－2，2－2)，N(6＋2，2＋2)，‎ ‎∴ MN＝＝4.‎ ‎②设存在直线m：x＝a满足题意，则圆心E，过E作直线x＝a的垂线，垂足为E′，设直线m与圆E的一个交点为G.可得|E′G|2＝|EG|2－|EE′|2，即|E′G|2＝|EA|2－|EE′|2＝－＝y＋＋a(x1＋4)－a2＝x1－4x1＋a(x1＋4)－a2＝(a－3)x1＋‎4a－a2.当a＝3时，|E′G|2＝3，此时直线m被以AM为直径的圆E所截得的弦长恒为定值2，因此存在直线m：x＝3满足题意．‎ ‎5. 如图，等边三角形OAB的边长为8，且其三个顶点均在抛物线E：x2＝2py(p>0)上．‎ ‎(1) 求抛物线E的方程；‎ ‎(2) 设动直线l与抛物线E相切于点P，与直线y＝－1相交于点Q.证明：以PQ为直径的圆恒过y轴上某定点．‎ 解：(1) 依题意，OB＝8，∠BOy＝30°.设B(x，y)，则x＝OBsin30°＝4，y＝OBcos30°＝12.因为点B(4，12)在x2＝2py上，所以(4)2＝2p×12，解得p＝2.故抛物线E的方程为x2＝4y.‎ ‎(2) 由(1)知y＝x2，y′＝x.设P(x0，y0)，‎ 则x0≠0，y0＝x，且l的方程为y－y0＝‎ x0(x－x0)，即y＝x0x－x.‎ 由得 所以Q为.‎ 设M(0，y1)，令·＝0对满足 y0＝x(x0≠0)的x0，y0恒成立．‎ 由于＝(x0，y0－y1)，‎ ＝，‎ 由·＝0，得－y0－y0y1＋y1＋y＝0，‎ 即(y＋y1－2)＋(1－y1)y0＝0.(*)‎ 由于(*)式对满足y0＝x(x0≠0)的y0恒成立，‎ 所以解得y1＝1.‎ 故以PQ为直径的圆恒过y轴上的定点M(0，1)．‎ ‎1. (文)已知抛物线y2＝2px，以过焦点的弦为直径的圆与抛物线准线的位置关系是________．‎ 答案：相切 解析：设抛物线焦点弦为AB，中点为M，准线为l，A1、B1分别为A、B在直线l上的射影，则|AA1|＝|AF|，|BB1|＝|BF|，于是M到l的距离d＝(|AA1|＋|BB1|)＝(|AF|＋|BF|)＝|AB|＝半径，故相切．‎ ‎　(理)下图是抛物线形拱桥，当水面在l时，拱顶离水面‎2 m，水面宽‎4 m．水位下降‎1 m后，水面宽________ m.‎ 答案：2 解析：设抛物线的方程为x2＝－2py，则点(2，－2)在抛物线上，代入可得p＝1，所以x2＝－2y.当y＝－3时，x2＝6，即x＝±，所以水面宽为2.‎ ‎2. (文)已知抛物线y2＝2px(p＞0)的焦点为F，P、Q是抛物线上的两个点，若△PQF是边长为2的正三角形，则p的值是________．‎ 答案：2± 解析：依题意得F，设P，Q(y1≠y2)．由抛物线定义及PF＝QF，得＋＝＋，所以y＝y，所以y1＝－y2.又PQ＝2，因此|y1|＝|y2|＝1，点P.又点P位于该抛物线上，于是由抛物线的定义得PF＝＋＝2，由此解得p＝2±.‎ ‎　(理)拋物线顶点在原点，它的准线过双曲线－＝1(a＞0，b＞0)的一个焦点，并与双曲线实轴垂直，已知拋物线与双曲线的一个交点为，求拋物线与双曲线方程．‎ 解：由题设知，拋物线以双曲线的右焦点为焦点，准线过双曲线的左焦点，∴p＝‎2c，设拋物线方程为y2＝‎4c·x.‎ ‎∵拋物线过点，∴6＝‎4c·.∴c＝1，故拋物线方程为y2＝4x.又双曲线－＝1过点，∴－＝1.又a2＋b2＝c2＝1，∴－＝1.∴a2＝或a2＝9(舍)．∴b2＝，故双曲线方程为4x2－＝1.‎ ‎3. (文)如图，过抛物线y2＝2px(p>0)的焦点F的直线l交抛物线于点A、B，交其准线于点C.若|BC|＝2|BF|，且|AF|＝3，则此抛物线的方程为________．‎ 答案：y2＝3x 解析：由抛物线定义，|BF|等于B到准线的距离．‎ 由|BC|＝2|BF|，得∠BCM＝30°.‎ 又|AF|＝3，从而A.‎ 由A在抛物线上，代入抛物线方程y2＝2px，解得p＝.‎ ‎　(理)如图所示，直线l1和l2相交于点M，l1⊥l2，点N∈l1，‎ 以A、B为端点的曲线段C上任一点到l2的距离与到点N的距离相等．若△AMN为锐角三角形，|AM|＝，|AN|＝3，且|NB|＝6，建立适当的坐标系，求曲线段C的方程．‎ 解：以直线l1为x轴，线段MN的垂直平分线为y轴，建立直角坐标系，由条件可知，曲线段C是以点N为焦点，以l2为准线的抛物线的一段．其中A、B分别为曲线段C的端点．‎ 设曲线段C的方程为y2＝2px(p＞0)(xA≤x≤xB，y＞0)，其中xA、xB为A、B的横坐标，p＝|MN|，∴M、‎ N.由|AM|＝，|AN|＝3，得＋2pxA＝17，①‎ ＋2pxA＝9.②‎ 联立①②，解得xA＝，代入①式，并由p＞0，解得或∵△AMN为锐角三角形，∴＞xA.‎ ‎∴由点B在曲线段C上，得xB＝|BN|－＝4.‎ 综上，曲线C的方程为y2＝8x(1≤x≤4，y>0)．‎ ‎4. (文)求满足下列条件的抛物线的标准方程，并求对应抛物线的准线方程．‎ ‎(1) 过点(－3，2)；‎ ‎(2) 焦点在直线x－2y－4＝0上．‎ 解：(1) 设所求抛物线的方程为y2＝－2px或x2＝2py(p＞0)．‎ ‎∵过点(－3，2)，∴4＝－2p(－3)或9＝2p·2.∴p＝或p＝.∴所求抛物线的方程为y2＝－x或x2＝y，前者的准线方程是x＝，后者的准线方程是y＝－.‎ ‎(2) 令x＝0得y＝－2，令y＝0得x＝4，∴抛物线的焦点为(4，0)或(0，－2)．当焦点为(4，0)时，＝4，∴p＝8，此时抛物线的方程为y2＝16x；焦点为(0，－2)时，＝2，∴p＝4，此时抛物线的方程为x2＝－8y.∴所求抛物线的方程为y2＝16x或x2＝－8y，对应的准线方程分别是x＝－4，y＝2.‎ ‎　(理)已知定点F(0，1)和直线l1：y＝－1，过定点F与直线l1相切的动圆圆心为点C.‎ ‎(1) 求动点C的轨迹方程；‎ ‎(2) 过点F的直线l2交轨迹于两点P、Q，交直线l1于点R，求·的最小值．‎ 解：(1) 由题设点C到点F的距离等于它到l1的距离，‎ ‎∴点C的轨迹是以F为焦点，l1为准线的抛物线．‎ ‎∴所求轨迹的方程为x2＝4y.‎ ‎(2) 由题意直线l2的方程为y＝kx＋1，‎ 与抛物线方程联立消去y，得x2－4kx－4＝0.‎ 记P(x1，y1)，Q(x2，y2)，则x1＋x2＝4k，x1x2＝－4.‎ 由直线PQ的斜率k≠0，易得点R的坐标为，‎ ·＝· ‎＝＋(kx1＋2)(kx2＋2)‎ ‎＝(1＋k2)x1x2＋(x1＋x2)＋＋4‎ ‎＝－4(1＋k2)＋4k＋＋4＝4＋8.‎ ‎∵k2＋≥2，当且仅当k2＝1时取到等号．‎ ‎∴·≥4×2＋8＝16，即·的最小值为16.‎ ‎1. 涉及抛物线上的点到焦点(准线)的距离问题，可优先考虑利用抛物线的定义转化为点到准线(焦点)的距离问题求解．‎ ‎2. 求抛物线的方程一般是利用待定系数法，即求p，但要注意判断标准方程的形式．‎ ‎3. 研究抛物线的几何性质时，一是注意定义转化应用；二是要结合图形分析，同时注意平面几何性质的应用．‎ ‎[备课札记]‎