2020届高考数学大二轮复习 第1部分 专题第1讲 空间几何体的三视图、表面积及体积练习

2020届高考数学大二轮复习 第1部分 专题第1讲 空间几何体的三视图、表面积及体积练习

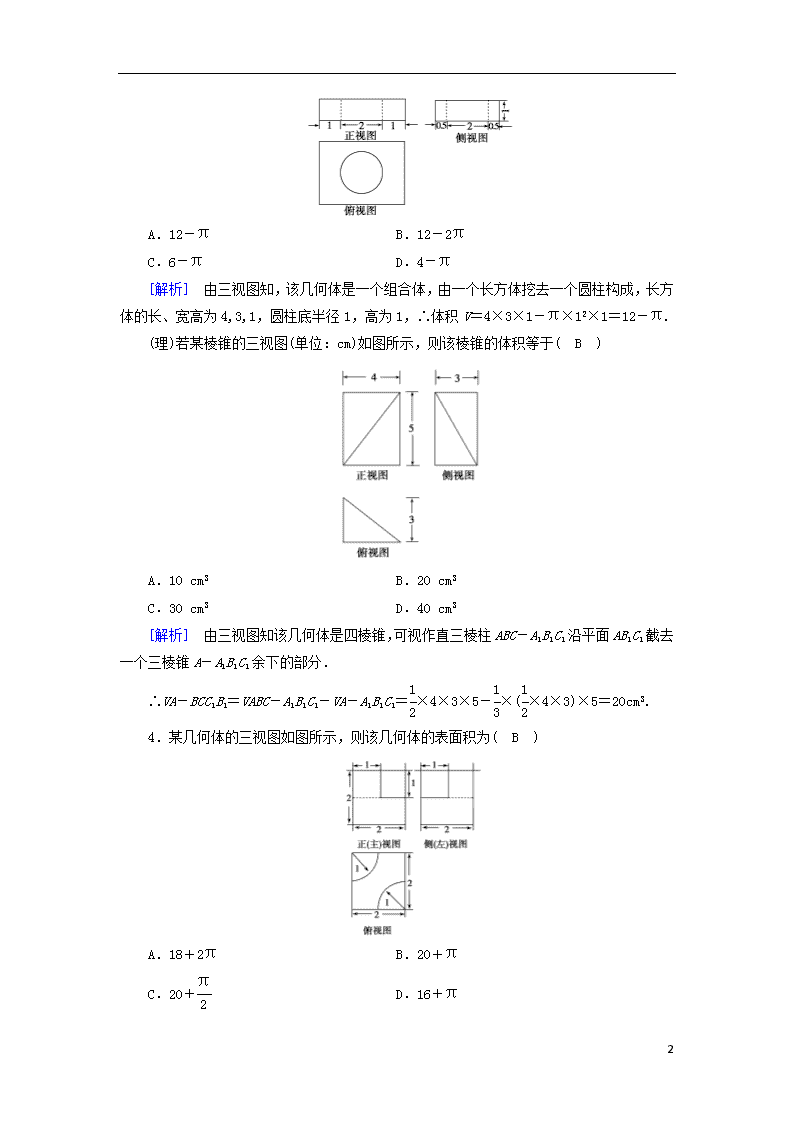
第一部分 专题五 第一讲 空间几何体的三视图、表面积及体积 A组 ‎1．如图1所示，是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图，其中DD1＝1，AB＝BC＝AA1＝2，若此几何体的俯视图如图2所示，则可以作为其正视图的是( C )‎ ‎[解析]　由直观图和俯视图知，正视图中点D1的射影是B1，所以正视图是选项C中的图形，A中少了虚线，故不正确．‎ ‎2．如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( C )‎ A．20π　　　 B．24π　　　　‎ C．28π　　　 D．32π ‎[解析]　该几何体是圆锥与圆柱的组合体，由三视图可知圆柱底面圆的半径r＝2，底面圆的周长c＝2πr＝4π，圆锥的母线长l＝＝4，圆柱的高h＝4，所以该几何体的表面积S表＝πr2＋ch＋cl＝4π＋16π＋8π＝28π，故选C．‎ ‎3．(文)一个几何体的三视图如图所示，则该几何体的体积为( A )‎ 10‎ A．12－π B．12－2π ‎ C．6－π D．4－π ‎[解析]　由三视图知，该几何体是一个组合体，由一个长方体挖去一个圆柱构成，长方体的长、宽高为4,3,1，圆柱底半径1，高为1，∴体积V＝4×3×1－π×12×1＝12－π.‎ ‎(理)若某棱锥的三视图(单位：cm)如图所示，则该棱锥的体积等于( B )‎ A．‎10 cm3 B．‎20 cm3‎ C．‎30 cm3 D．‎40 cm3‎ ‎[解析]　由三视图知该几何体是四棱锥，可视作直三棱柱ABC－A1B‎1C1沿平面AB‎1C1截去一个三棱锥A－A1B‎1C1余下的部分．‎ ‎∴VA－BCC1B1＝VABC－A1B‎1C1－VA－A1B‎1C1＝×4×3×5－×(×4×3)×5＝‎20cm3.‎ ‎4．某几何体的三视图如图所示，则该几何体的表面积为( B )‎ A．18＋2π B．20＋π C．20＋ D．16＋π 10‎ ‎[解析]　由三视图可知，这个几何体是一个边长为2的正方体割去了相对边对应的两个半径为1、高为1的圆柱体，其表面积相当于正方体五个面的面积与两个圆柱的侧面积的和，即该几何体的表面积S＝4×5＋2×2π×1×1×＝20＋π.‎ 故选B．‎ ‎5．(2018·双鸭山一模)一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的外接球的表面积为( A )‎ A． B． C．4 D．2π ‎[解析]　由已知几何体的正视图是一个正三角形，侧视图和俯视图均为三角形，可得该几何体有一个侧面PAC垂直于底面，高为，底面是一个等腰直角三角形的三棱锥，如图．‎ 则这个几何体的外接球的球心O在高线PD上，且是等边三角形PAC的中心，‎ 这个几何体的外接球的半径R＝PD＝.‎ 则这个几何体的外接球的表面积为S＝4πR2＝4π×()2＝.‎ ‎6．如图，正方体ABCD－A1B‎1C1D1的棱长为1，E，F分别为线段AA1，B‎1C上的点，则三棱锥D1－EDF的体积为.‎ 10‎ ‎[解析]　利用三棱锥的体积公式直接求解．‎ VD1－EDF＝VF－DD1E＝SD1DE·AB＝××1×1×1＝.‎ ‎7．已知E，F分别是矩形ABCD的边BC与AD的中点，且BC＝2AB＝2，现沿EF将平面ABEF折起，使平面ABEF⊥平面EFDC，则三棱锥A－FEC外接球的体积为π.‎ ‎[解析]　如图，平面ABEF⊥平面EFDC，AF⊥EF，‎ 所以AF⊥平面ECDF，将三棱锥A－FEC补成正方体ABC′D′－FECD．‎ 依题意，其棱长为1，外接球的半径R＝，‎ 所以外接球的体积V＝πR3＝π·()3＝π.‎ ‎8．(文)如图，三棱柱ABC－A1B‎1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.‎ ‎(1)证明：AB⊥A‎1C；‎ ‎(2)若AB＝CB＝2，A‎1C＝，求三棱柱ABC－A1B‎1C1的体积．‎ ‎[解析]　(1)取AB的中点O，连接OC，OA1，A1B．‎ 因为CA＝CB，所以OC⊥AB．‎ 由于AB＝AA1，∠BAA1＝60°，故△AA1B为等边三角形，所以OA1⊥AB．‎ 因为OC∩OA1＝O，所以AB⊥平面OA‎1C．‎ 又A‎1C⊂平面OA‎1C，故AB⊥A‎1C．‎ 10‎ ‎(2)由题设知△ABC与△AA1B都是边长为2的等边三角形，所以OC＝OA1＝.‎ 又A‎1C＝，则A‎1C2＝OC2＋OA，故OA1⊥OC．‎ 因为OC∩AB＝O，所以OA1⊥平面ABC，OA1为三棱柱ABC－A1B‎1C1的高．‎ 又△ABC的面积S△ABC＝.故三棱柱ABC－A1B‎1C1的体积V＝S△ABC×OA1＝3.‎ ‎(理)如图，四棱锥P－ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB＝BC＝AD，∠BAD＝∠ABC＝90°.‎ ‎(1)证明：直线BC∥平面PAD；‎ ‎(2)若△PCD的面积为2，求四棱锥P－ABCD的体积．‎ ‎[解析]　(1)证明：在平面ABCD内，因为∠BAD＝∠ABC＝90°，所以BC∥AD．‎ 又BC⊄平面PAD，AD⊂平面PAD，‎ 故BC∥平面PAD．‎ ‎(2)如图，取AD的中点M，连接PM，CM.‎ 由AB＝BC＝AD及BC∥AD，∠ABC＝90°得四边形ABCM为正方形，则CM⊥AD．‎ 因为侧面PAD为等边三角形且垂直于底面ABCD，‎ 平面PAD∩平面ABCD＝AD，‎ 所以PM⊥AD，PM⊥底面ABCD．‎ 因为CM⊂底面ABCD，‎ 所以PM⊥CM.‎ 设BC＝x，则CM＝x，CD＝x，PM＝x，PC＝PD＝2x.‎ 如图，取CD的中点N，连接PN，则PN⊥CD，‎ 所以PN＝x.‎ 因为△PCD的面积为2，‎ 所以×x×x＝2，‎ 解得x＝－2(舍去)或x＝2.‎ 于是AB＝BC＝2，AD＝4，PM＝2.‎ 所以四棱锥P－ABCD的体积V＝××2＝4.‎ 10‎ B组 ‎1．(文)某三棱锥的三视图如图所示，则该三棱锥的体积为( D )‎ A．60 B．30 ‎ C．20 D．10‎ ‎[解析]　‎ 由三视图画出如图所示的三棱锥P－ACD，过点P作PB⊥平面ACD于点B，连接BA，BD，BC，根据三视图可知底面ABCD是矩形，AD＝5，CD＝3，PB＝4，所以V三棱锥P－ACD＝××3×5×4＝10.‎ 故选D．‎ ‎(理)某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为( B )‎ A．3 B．2 ‎ C．2 D．2‎ ‎[解析]　在正方体中还原该四棱锥，如图所示，‎ 可知SD为该四棱锥的最长棱．‎ 由三视图可知正方体的棱长为2，‎ 故SD＝＝2.‎ 故选B．‎ 10‎ ‎2．(2018·宜宾一模)三棱锥A－BCD内接于半径为2的球O，BC过球心O，当三棱锥A－BCD体积取得最大值时，三棱锥A－BCD的表面积为( D )‎ A．6＋4 B．8＋2 C．4＋6 D．8＋4 ‎[解析]　由题意，BC为直径，△BCD的最大面积为×4×2＝4，‎ 三棱锥A－BCD体积最大时，AO⊥平面BCD，三棱锥的高为2，‎ 所以三棱锥A－BCD的表面积为4×2＋2××2×＝8＋4.‎ ‎3．三棱锥P－ABC中，PA⊥平面ABC且PA＝2，△ABC是边长为的等边三角形，则该三棱锥外接球的表面积为( C )‎ A． B．4π ‎ C．8π D．20π ‎[解析]　由题意得，此三棱锥外接球即为以△ABC为底面、以PA为高的正三棱柱的外接球，因为△ABC的外接圆半径r＝××＝1，外接球球心到△ABC的外接圆圆心的距离d＝1，所以外接球的半径R＝＝，所以三棱锥外接球的表面积S＝4πR2＝8π，‎ 故选C．‎ ‎4．某四面体的三视图如图所示，正视图、俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大的为( B )‎ A．2 B．2 ‎ C．4 D．2 ‎[解析]　如图，四面体的直观图是棱长为2的正方体ABCD－MNPQ中的三棱锥Q－BCN，且QB＝＝2，NC＝QN＝QC＝2，四面体Q－BCN各面的面积分别为S△QBN＝S△QBC＝×2×2＝2，S△BCN＝×2×2＝2，S△QCN＝×(2)2＝2，‎ 10‎ 面积最大为2.‎ ‎5．三棱锥S－ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为( B )‎ A．2 B．4 ‎ C． D．16 ‎[解析]　由已知中的三视图可得SC⊥平面ABC，且底面△ABC为等腰三角形，‎ 在△ABC中AC＝4，AC边上的高为2，‎ 故BC＝4，‎ 在Rt△SBC中，由SC＝4，‎ 可得SB＝4.‎ ‎6．设甲、乙两个圆柱的底面积分别为S1，S2，体积分别为V1，V2.若它们的侧面积相等且＝，则的值是.‎ ‎[解析]　设甲、乙两个圆柱的底面半径分别为r1，r2，高分别为h1，h2，则有2πr1h1＝2πr2h2，即r1h1＝r2h2，又＝，∴＝，∴＝，则＝()2＝.‎ ‎7．已知在直角梯形ABCD中，AB⊥AD，CD⊥AD，AB＝2AD＝2CD＝2，将直角梯形ABCD沿AC折叠成三棱锥D－ABC，当三棱锥D－ABC的体积取最大值时，其外接球的体积为π.‎ ‎[解析]　当平面DAC⊥平面ABC时，三棱锥D－ABC的体积取最大值．此时易知BC⊥平面DAC，∴BC⊥AD，又AD⊥DC，∴AD⊥平面BCD，∴AD⊥BD，取AB的中点O，易得OA＝OB＝OC＝OD＝1，故O为所求外接球的球心，故半径r＝1，体积V＝πr3＝π.‎ ‎8．(文)如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD．‎ ‎(1)证明：平面AEC⊥平面BED；‎ ‎(2)若∠ABC＝120°，AE⊥EC，三棱锥E____ACD的体积为，求该三棱锥的侧面积．‎ 10‎ ‎[解析]　(1)证明：因为四边形ABCD为菱形，所以AC⊥BD．‎ 因为BE⊥平面ABCD，所以AC⊥BE.‎ 故AC⊥平面BED．又AC⊂平面AEC，‎ 所以平面AEC⊥平面BED．‎ ‎(2)设AB＝x，在菱形ABCD中，‎ 由∠ABC＝120°，可得AG＝GC＝x，‎ GB＝GD＝.‎ 因为AE⊥EC，‎ 所以在Rt△AEC中，可得EG＝x.‎ 由BE⊥平面ABCD，知△EBG为直角三角形，可得BE＝x.‎ 由已知得，三棱锥EACD的体积 VEACD＝×AC·GD·BE＝x3＝.‎ 故x＝2.从而可得AE＝EC＝ED＝.‎ 所以△EAC的面积为3，△EAD的面积与△ECD的面积均为.‎ ‎ 故三棱锥EACD的侧面积为3＋2.‎ ‎(理)如图，在多面体ABCDEF中，底面ABCD是边长为2的正方形，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF＝3，G和H分别是CE和CF的中点．‎ ‎(1)求证：AC⊥平面BDEF；‎ ‎(2)求证：平面BDGH//平面AEF；‎ ‎(3)求多面体ABCDEF的体积．‎ ‎[解析]　(1)证明：因为四边形ABCD是正方形，‎ 10‎ 所以AC⊥BD．‎ 又因为平面BDEF⊥平面ABCD，平面BDEF∩平面ABCD＝BD，‎ 且AC⊂平面ABCD，‎ 所以AC⊥平面BDEF.‎ ‎(2)证明：在△CEF中，因为G、H分别是CE、CF的中点，‎ 所以GH∥EF，‎ 又因为GH⊄平面AEF，EF⊂平面AEF，‎ 所以GH∥平面AEF.‎ 设AC∩BD＝O，连接OH，‎ 在△ACF中，因为OA＝OC，CH＝HF，‎ 所以OH∥AF，‎ 又因为OH⊄平面AEF，AF⊂平面AEF，‎ 所以OH∥平面AEF.‎ 又因为OH∩GH＝H，OH，GH⊂平面BDGH，‎ 所以平面BDGH∥平面AEF.‎ ‎(3)解：由(1)，得AC⊥平面BDEF，‎ 又因为AO＝，四边形BDEF的面积SBDEF＝3×2＝6，‎ 所以四棱锥A－BDEF的体积V1＝×AO×SBDEF＝4.‎ 同理，四棱锥C－BDEF的体积V2＝4.‎ 所以多面体ABCDEF的体积V＝V1＋V2＝8.‎ 10‎