高中新课程数学新课标人教A版必修五 不等式高考真题
第三章 不等式
本章归纳整合
高考真题
1.(2011·陕西卷)设0
0,即>a,故选B.
答案 B
2.(2011·广东卷)不等式2x2-x-1>0的解集是 ( ).
A. B.(1,+∞)
C.(-∞,1)∪(2,+∞) D.∪(1,+∞)
解析 ∵2x2-x-1=(2x+1)(x-1),∴由2x2-x-1>0得(2x+1)(x-1)>0,解得x>1或x<-,∴不等式的解集为∪(1,+∞).
答案 D
3.(2011·福建卷)若关于x的方程x2+mx+1=0有两个不相等的实数根,则实数m的取值范围是 ( ).
A.(-1,1) B.(-2,2)
C.(-∞,-2)∪(2,+∞) D.(-∞,-1)∪(1,+∞)
解析 ∵方程x2+mx+1=0有两个不相等的实数根,
∴Δ=m2-4>0,∴m>2或m<-2.
答案 C
4.(2011·天津卷)设变量x,y满足约束条件则目标函数z=3x-y的最大值为 ( ).
A.-4 B.0 C. D.4
解析 表示的平面区域如图所
示.
z=3x-y在(2,2)取得最大值.
zmax=3×2-2=4.
答案 D
5.(2011·浙江卷)设实数x,y满足不等式组且x,y为整数,则3x+4y的最小值是 ( ).
A.14 B.16
C.17 D.19
解析 作出可行域,如图中阴影部分所示,点
A(3,1)不在可行域内,利用网格易得点(4,1)符
合条件,故3x+4y的最小值是3×4+4×1=
16.
答案 B
6.(2011·重庆卷)已知a>0,b>0,a+b=2,则y=+的最小值是 ( ).
A. B.4 C. D.5
解析 ∵a+b=2,∴=1,
∴+==+≥+2 =当且仅当=,即b=2a时,“=”成立,故y=+的最小值为.
答案 C
7.(2011·北京卷)某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x件,则平均仓储时间为天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品 ( ).
A.60件 B.80件 C.100件 D.120件
解析 设每件产品的平均费用为y元,由题意,得
y=+≥2 =20.
当且仅当=(x>0),即x=80时“=”成立,故选B.
答案 B
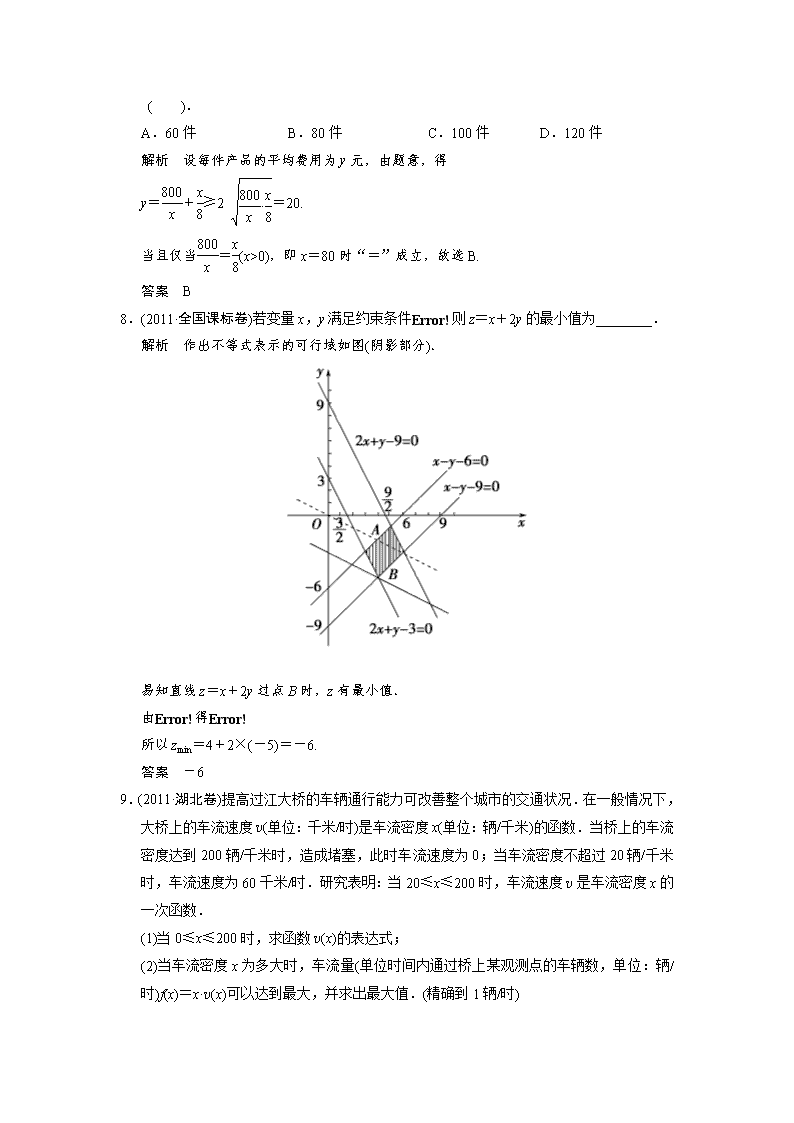
8.(2011·全国课标卷)若变量x,y满足约束条件则z=x+2y的最小值为________.
解析 作出不等式表示的可行域如图(阴影部分).
易知直线z=x+2y过点B时,z有最小值.
由得
所以zmin=4+2×(-5)=-6.
答案 -6
9.(2011·湖北卷)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/时)
解 (1)由题意,当0≤x≤20时,v(x)=60;当20≤x≤200时,设v(x)=ax+b,再由已知,得
解得
故函数v(x)的表达式为v(x)=
(2)依题意并由(1),可得f(x)=
当0≤x≤20时,f(x)为增函数,故当x=20时,其最大值为60×20=1 200;
当20
查看更多