高考数学真题汇编含答案概率与统计

高考数学真题汇编含答案概率与统计

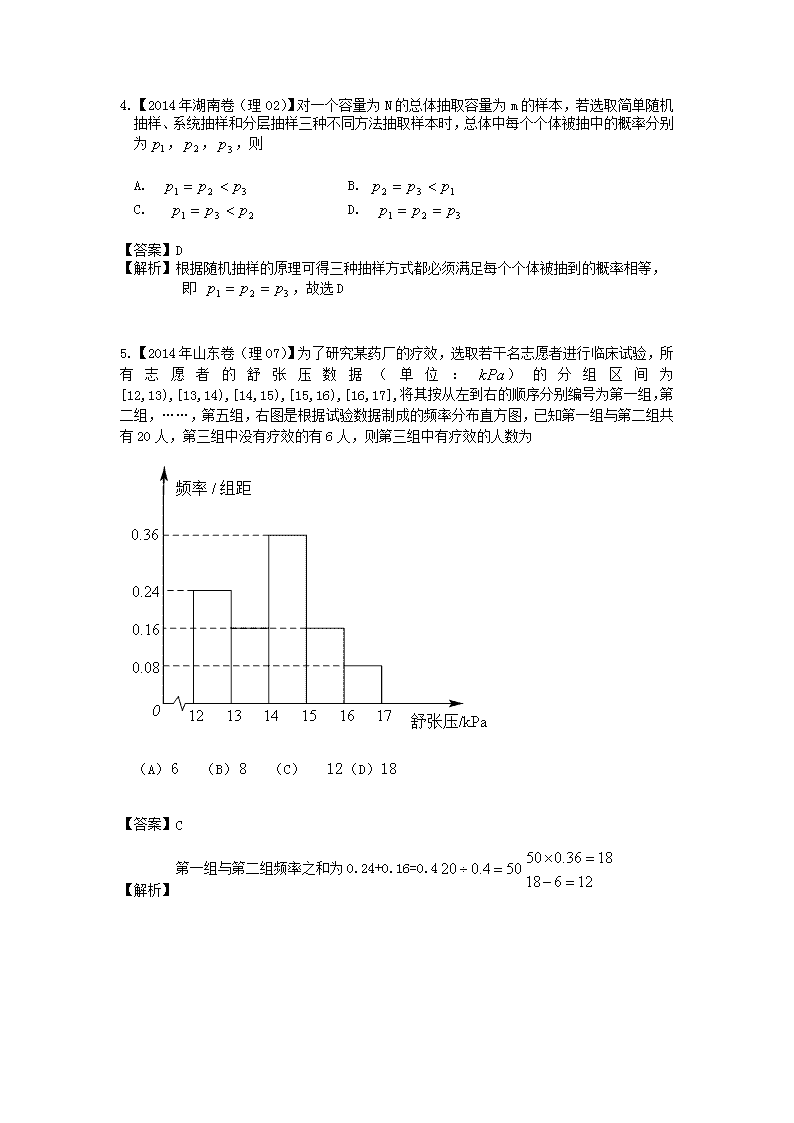
‎2014年全国高考理科数学试题分类汇编(纯word解析版)‎ ‎ 八、概率与统计（逐题详解）‎ ‎ 第I部分 ‎ ‎1.【2014年陕西卷（理06）】从正方形四个顶点及其中心这5个点中，任取2个点，则这2个点的距离不小于该正方形边长的概率为（ ）‎ ‎ ‎ ‎【答案】 C ‎【解析】‎ ‎2.【2014年重庆卷（理03）】已知变量与正相关，且由观测数据算得样本平均数，，则由观测的数据得线性回归方程可能为（ ）‎ ‎ ‎ ‎ ‎ ‎【答案】A ‎【解析】根据正相关知回归直线的斜率为正，排除，回归直线经过点，故选 ‎3.【2014年陕西卷（理09）】设样本数据的均值和方差分别为1和4，若（为非零常数， ），则的均值和方差分别为（ ）‎ （A） ‎ （B） （C） （D） ‎ ‎【答案】 A ‎【解析】‎ ‎4.【2014年湖南卷（理02）】对一个容量为N的总体抽取容量为m的样本，若选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为，，，则 A. B. ‎ ‎ C. D. ‎ ‎ ‎ ‎【答案】D ‎【解析】根据随机抽样的原理可得三种抽样方式都必须满足每个个体被抽到的概率相等，‎ 即 ，故选D ‎5.【2014年山东卷（理07）】为了研究某药厂的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据（单位：）的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组，第二组，……，第五组，右图是根据试验数据制成的频率分布直方图，已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为 ‎ （A） （B） （C） （D）‎ ‎ ‎ ‎【答案】C ‎【解析】第一组与第二组频率之和为0.24+0.16=0.4‎ ‎6.【2014年全国新课标Ⅰ（理05）】4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率 ‎. . . .‎ ‎【答案】：D ‎【解析】：4位同学各自在周六、周日两天中任选一天参加公益活动共有种，‎ 周六、周日都有同学参加公益活动有两种情况：①一天一人一天三人有种；②每天2人有种，则周六、周日都有同学参加公益活动的概率为；或间接解法：4位同学都在周六或周日参加公益活动有2种，则周六、周日都有同学参加公益活动的概率为；选D. ‎ ‎7.【2014年全国新课标Ⅱ（理05）】某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（ ）‎ A. 0.8 B. 0.75 C. 0.6 D. 0.45‎ ‎【答案】 A ‎【解析】‎ ‎8.【2014年广东卷（理06）】已知某地区中小学生人数和近视情况分别如图1和图2所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为 A. 200,20　　　 B. 100,20　　 ‎ C. 200,10　　 D. 100,10‎ ‎【答案】A ‎【解析】由题意知：该地区中小学生总人数为：‎ 人，所以样本容量为，应抽取高中生人数为：，所以抽取的高中生近视人数为人.故选A.‎ ‎9.【2014年湖北卷（理04）】根据如下样本数据 x ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ y ‎4.0‎ ‎2.5‎ ‎-0.5‎ ‎0.5‎ ‎-2.0‎ ‎-3.0‎ 得到的回归方程为，则 A. B. C. D.‎ ‎【答案】 B ‎【解析】画出散点图如图所示，y的值大致随x的增加而减小，‎ 因而两个变量呈负相关，所以，‎ 10. ‎【2014年湖北卷（理07）】由不等式确定的平面区域记为，不等式，确定的平面区域记为，在中随机取一点，则该点恰好在内的概率为（ ）‎ A. ‎ B. C. D.‎ ‎【答案】 D ‎【解析】依题意，不等式组表示的平面区域如图，‎ 由几何概型概率公式知，该点落在内的概率为.‎ ‎11.【2014年江西卷（理06）】某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系，随机抽查52名中学生，得到统计数据如表1至表4，则与性别有关联的可能性最大的变量是 ‎ ‎ ‎ ‎ ‎【答案】D ‎【解析】根据独立性检验相关分析知，阅读量与性别相关数据较大，选D ‎12.【2014年浙江卷（理09）】已知甲盒中仅有1个球且为红球，乙盒中有个红球和个蓝球，，从乙盒中随机抽取，个球放入甲盒中.‎ ‎（）放入个球后，甲盒中含有红球的个数记为，；‎ ‎（）放入个球后，从甲盒中取1个球是红球的概率记为，.则 A.， B.，‎ C.， D.，‎ ‎【答案】A ‎【解析】，，‎ ‎，所以P1＞P2；由已知ξ1的取值为1、2，ξ2的取值为1、2、3，所以 == ，E（ξ1）﹣E（ξ2）=．故选A ‎ 第II部分 ‎ ‎13.【2014年辽宁卷（理14）】正方形的四个顶点分别在抛物线和上，如图所示，若将一个质点随机投入正方形ABCD中，学科网则质点落在阴影区域的概率是 .‎ ‎【答案】‎ ‎【解析】∵A（﹣1，﹣1），B（1，﹣1），C（1，1），D（﹣1，1），‎ ‎∴正方体的ABCD的面积S=2×2=4，‎ 根据积分的几何意义以及抛物线的对称性可知阴影部分的面积 S=2=2=2[（1﹣）﹣（﹣1+）]=2×=，‎ 则由几何槪型的概率公式可得质点落在图中阴影区域的概率是．故答案为：‎ ‎14.【2014年广东卷（理11）】从0,1,2,3,4,5,6,7,8，9中任取七个不同的数，则这七个数的中位数是6的概率为 。‎ ‎【答案】‎ ‎【解析】由题意得：所有的基本事件有个，其中中位数是6的事件有个，所求概率为=‎ ‎15.【2014年江西卷（理12）】10件产品中有7件正品，3件次品，从中任取4件，则恰好取到1件次品的概率是________.‎ ‎【答案】 【解析】‎ ‎16.【2014年天津卷（理09）】某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方法，从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为，则应从一年级本科生中抽取____名学生.‎ ‎【答案】60‎ ‎【解析】由分层抽样的方法可得，从一年级本科生中抽取学生人数为300×＝60‎ ‎17.【2014年江苏卷（理04）】从这个数中一次随机地取2个数，则所取2个数的乘积为的概是 ．‎ ‎【答案】‎ ‎【解析】将随机选取2个数的所有情况“不重不漏”‎ 的列举出来：（1，2），（1，3）（1，6），（2，3），（2，6），（3，6），共6种情况，满足题目乘积为6的要求的是（1，6）和（2，3），则概率为。‎ ‎18.【2014年江苏卷（理06）】在底部周长的树木进行研究，频率分布直方图如图所示，则在抽测的60株树木中，有 株树木的底部周长小于100cm.‎ ‎【答案】24‎ ‎【解析】从图中读出底部周长在的频率为，底部周长在的频率为，样本容量为60株，株是满足题意的。‎ ‎80 90 100 110 120 130 ‎ ‎0.030 ‎ ‎0.025 ‎ ‎0.020 ‎ ‎0.015 ‎ ‎0.010 ‎ 底部周长 cm ‎ 频率/组距 ‎ 第6题图 ‎ ‎19.【2014年上海卷（理10）】为强化安全意识，某商场拟在未来的连续天中随机选择天进行紧急疏散演练，则 选择的天恰好为连续天的概率是 （结果用最简分数表示）.‎ ‎【答案】‎ ‎【解析】：‎ ‎20.【2014年上海卷（理13）】 某游戏的得分为，随机变量 表示小白玩该游戏的得分. 若，则小白得分的概率至少为 .‎ ‎【答案】0.2‎ ‎【解析】：设得分的概率为，∴，‎ 且，∴，与前式相减得：‎ ‎，∵，∴，即 ‎21.【2014年浙江卷（理12）】随机变量的取值为0，1，2，若，，则_____.‎ ‎【答案】‎ ‎【解析】设P（ξ=1）=p，P（ξ=2）=q，则由已知得p+q=，，解得，，‎ 所以．故答案为：‎ 第III部分 ‎22.【2014年陕西卷（理19）】（本小题满分12分）‎ 在一块耕地上种植一种作物，每季种植成本为1000元，此作物的市场价格和这块地上 的产量具有随机性，且互不影响，其具体情况如下表：‎ 作物市场价格（元/kg）‎ ‎6‎ ‎10‎ 概率 ‎0.4‎ ‎0.6‎ 作物产量（kg）‎ ‎300‎ ‎500‎ 概率 ‎0.5‎ ‎0.5‎ ‎ （1）设表示在这块地上种植1季此作物的利润，求的分布列；‎ ‎ （2）若在这块地上连续3季种植此作物，求这3季中至少有2季的利润不少于2000元 ‎ 的概率.‎ ‎ 解（I）设A表示事件“作物产量为300kg”，B表示事件“作物市场价格为6元/kg”，由题设知P(A)=0.5，P(B)=0.4‎ ‎ 利润=产量市场价格 - 成本，‎ ‎ X所有可能地取值为 ‎ 500 X 10 - 1000 = 4000，500 X 6 - 1000 = 2000.‎ ‎ 300 X 10 - 1000 = 2000， 300 X 6 - 1000=800.‎ ‎ P(X = 4000) =P = (1 - 0.5) X (1 - 0.4) = 0.3.‎ ‎ P(X = 2000) =P + P = (1- 0.5) X 0.4 X 0.5 X (1 - 0.4) = 0.5.‎ ‎ P(X = 800) =P = 0.5 X 0.4 = 0.2.‎ ‎ 所以X 的分布列为 ‎ （II）设C1，C2 ，C3相互独立，由（I）知，‎ ‎ P（G）= P(X = 4000) + P(X = 2000) = 0.3+0.5 = 0.8 (= 1,2,3),‎ ‎ 3季的利润均不少于2000元的概率为 ‎ P()+P()+P()=3X0.82X0.2=0.384,‎ ‎ 所以，这3季中至少有2季的利润不少于2000元的概率为 ‎ 0.512+0.384=0.896.‎ ‎23.【2014年重庆卷（理18）】一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1,3张卡片上的数字 ‎ 是2,2张卡片上的数字是3，从盒中任取3张卡片.‎ ‎（1）求所取3张卡片上的数字完全相同的概率;‎ ‎（2）表示所取3张卡片上的数字的中位数，求的分布列（注：若三个数满足 ‎ ，则称为这三个数的中位数）.‎ 解：（1）所求概率 ‎（2）；‎ ‎24.【2014年安徽卷（理17）】（本小题满分12分）‎ 甲乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完局仍未出现连胜，则判定获胜局数多者赢得比赛，假设每局甲获胜的概率为，乙获胜的概率为，各局比赛结果相互独立．‎ ‎（Ⅰ）求甲在局以内（含局）赢得比赛的概率；‎ ‎（Ⅱ）记为比赛决出胜负时的总局数，求的分布列和均值（数学期望）．‎ ‎【解析】（Ⅰ）设事件表示“甲在第局比赛结束时赢得比赛”，根据题意得：‎ ‎ ；；‎ ‎ 因此，甲在局以内（含局）赢得比赛的概率 ‎（Ⅱ）的所有可能取值集合为 ‎ ； ‎ ‎；‎ ‎ ；‎ ‎（或）‎ ‎ 的分布列为 ‎ ‎ ‎ ‎ ‎25.【2014年福建卷（理18）】为回馈顾客，某商场拟通过摸球兑奖的方式对1000位顾客进行奖励，规定：每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球，球上所标的面值之和为该顾客所获的奖励额．‎ ‎（1）若袋中所装的4个球中有1个所标的面值为50元，其余3个均为10元，求：‎ ‎①顾客所获的奖励额为60元的概率；‎ ‎②顾客所获的奖励额的分布列及数学期望；‎ ‎（2）商场对奖励总额的预算是60000元，并规定袋中的4个球只能由标有面值10元和50元的两种球组成，或标有面值20元和40元的两种球组成．为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡，请对袋中的4个球的面值给出一个合适的设计，并说明理由．‎ ‎　‎ 解：（1）设顾客所获取的奖励额为X，‎ ‎①依题意，得P（X=60）=，即顾客所获得奖励额为60元的概率为，‎ ‎②依题意得X得所有可能取值为20，60，P（X=60）=，P（X=20）=，‎ X ‎60‎ ‎20‎ P 即X的分布列为 ‎ 所以这位顾客所获的奖励额的数学期望为E（X）=20×+60×=40‎ ‎（2）根据商场的预算，每个顾客的平均奖励额为60元，所以先寻找期望为60元的可能方案．‎ 对于面值由10元和50元组成的情况，如果选择（10，10，10，50）的方案，因为60元是面值之和的最大值，所以数学期望不可能为60元，‎ 如果选择（50，50，50，10）的方案，因为60元是面值之和的最小值，所以数学期望也不可能为60元，‎ 因此可能的方案是（10，10，50，50）记为方案1，‎ 对于面值由20元和40元的组成的情况，同理可排除（20，20，20，40）和（40，40，40，20）的方案，所以可能的方案是（20，20，40，40），记为方案2，‎ 以下是对这两个方案的分析：‎ 对于方案1，即方案（10，10，50，50）设顾客所获取的奖励额为X1，则X1的分布列为 ‎ X1‎ ‎60‎ ‎20‎ ‎100‎ P X1 的数学期望为E（X1）=．‎ X1 的方差D（X1）==，‎ 对于方案2，即方案（20，20，40，40）设顾客所获取的奖励额为X2，则X2的分布列为 ‎ X2‎ ‎40‎ ‎20‎ ‎80‎ P X2 的数学期望为E（X2）==60，‎ X2 的方差D（X2）=差D（X1）=．‎ 由于两种方案的奖励额的数学期望都符合要求，但方案2奖励额的方差比方案1小，所以应该选择方案2．‎ ‎26.【2014年湖南卷（理17）】 (本小题满分12分)‎ ‎ 某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别是和. 现安排甲组研发新产品A，乙组研发新产品B. 设甲、乙两组的研发相互独立. ‎ ‎（1）求至少有一种新产品研发成功的概率；‎ ‎（2）若新产品A研发成功，预计企业可获利润120万元；若新产品B研发成功，预计企业可获得利润100万元. 求该企业可获利润的分布列和数学期望. ‎ 解： 记E＝{甲组研发新产品成功}，F＝{乙组研发新产品成功}，由题可知 ‎ , ，，.‎ 且事件E与F，E与，与，与都相互独立.‎ ‎(1) 记H＝{至少有一种新产品研发成功}，则，于是 ‎，故所求概率为.‎ ‎（2）设企业可获利润为（万元），则的可能取值为0，100，120，220. 又因 ‎，，‎ ‎，.‎ 故所求分布列为 X ‎0‎ ‎100‎ ‎120‎ ‎220‎ P 数学期望为 .‎ ‎27.【2014年辽宁卷（理18）】（本小题满分12分）‎ 一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图，如图所示：‎ 将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立.‎ ‎（1）求在未来连续3天里，有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率；‎ ‎（2）用X表示在未来3天里日销售量不低于100个的天数，求随机变量X的分布列，期望及方差.‎ ‎（Ⅰ）设表示事件“日销售量不低于100个”，表示事件“日销售量低于50个”，B表示事件“在未来连续3天里有连续2天日销售量不低于100个且另一天的日销售量低于50个”.因此 ‎ .‎ ‎. .‎ ‎（Ⅱ）X的可能取值为0,1,2,3.相应的概率为 ‎,‎ ‎,‎ ‎,‎ ‎,‎ 分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎0.064‎ ‎0.288‎ ‎0.432‎ ‎0.216‎ 因为X~B(3,0.6),所以期望为E(X)=3×0.6=1.8，方差D（X）=3×0.6×（1-0.6）=0.72‎ ‎28.【2014年全国大纲卷（20）】（本小题满分12分）‎ 设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为，各人是否需使用设备相互独立.‎ ‎（1）求同一工作日至少3人需使用设备的概率；‎ ‎（2）X表示同一工作日需使用设备的人数，求X的数学期望.‎ 解：记表示事件：同一工作日乙、丙中恰有人需使用设备，‎ 表示事件：甲需使用设备 表示事件：丁需使用设备 表示事件：同一工作日至少3人需使用设备 ‎（1）‎ 所以 ‎（2）的可能取值为，，，，‎ ‎．‎ ‎，‎ ‎，‎ ‎，‎ 所以的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 数学期望 ．‎ ‎29.【2014年山东卷（理18）】（本小题满分12分）‎ ‎ 乒乓球台面被球网分成甲、乙两部分.如图，甲上有两个不相交的区域，乙被划分为两个不相交的区域.某次测试要求队员接到落点在甲上的来球后向乙回球.规定：回球一次，落点在上的概率为，在上的概率为.假设共有两次来球且落在上各一次，小明的两次回球互不影响.求：‎ ‎（I）小明两次回球的落点中恰有一次的落点在乙上的概率；‎ ‎（II）两次回球结束后，小明得分之和的分布列与数学期望.‎ 解：（I）设恰有一次的落点在乙上这一事件为 ‎（II）‎ ‎ ‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎6‎ ‎30.【2014年四川卷（理17）】一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分（即获得分）。设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立。‎ ‎（1）设每盘游戏获得的分数为，求的分布列；‎ ‎（2）玩三盘游戏，至少有一盘出现音乐的概率是多少？‎ ‎（3）玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了。请运用概率统计的相关知识分析分数减少的原因。‎ 解：（1）可能取值有，10，20，100‎ ‎，，‎ ‎，‎ 故分布列为 ‎10‎ ‎20‎ ‎100‎ P ‎（2）由（1）知：每盘游戏出现音乐的概率是 则玩三盘游戏，至少有一盘出现音乐的概率是 ‎（3）由（1）知，每盘游戏获得的分数为的数学期望是 分 这说明每盘游戏平均得分是负分，由概率统计的相关知识可知：许多人经过若干盘游戏后，与最初的分数相比，分数没有增加反而会减少。‎ ‎31.【2014年天津卷（理16）】（本小题满分13分）‎ 某大学志愿者协会有6名男同学，4名女同学.在这10名同学中，3名同学来自数学学院，其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学，到希望小学进行支教活动（每位同学被选到的可能性相同）.‎ ⑴求选出的3名同学是来自互不相同学院的概率；‎ ⑵设为选出的3名同学中女同学的人数，求随机变量的分布列和数学期望.‎ 解：(1)设“选出的3名同学是来自互不相同的学院”为事件A，则 P(A)＝＝，‎ 所以选出的3名同学是来自互不相同学院的概率为.‎ ‎(2)随机变量X的所有可能值为0，1，2，3.‎ P(X＝k)＝(k＝0，1，2，3)，‎ 所以随机变量X的分布列是 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 随机变量X的数学期望E(X)＝0×＋1×＋2×＋3×＝.‎ ‎32.【2014年全国新课标Ⅰ（理18）】(本小题满分12分)从某企业的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：‎ ‎(Ⅰ)求这500件产品质量指标值的样本平均数和样本方差（同一组数据用该区间的中点值作代表）；‎ ‎（Ⅱ）由频率分布直方图可以认为，这种产品的质量指标值服从正态分布，其中近似为样本平均数，近似为样本方差.‎ ‎(i)利用该正态分布，求；‎ ‎（ii）某用户从该企业购买了100件这种产品，记表示这100件产品中质量指标值为于区间（187.8,212.2）的产品件数，利用（i）的结果，求.‎ 附：≈12.2.‎ 若～，则=0.6826，=0.9544.‎ ‎【解析】：(Ⅰ) 抽取产品质量指标值的样本平均数和样本方差分别为 ‎ …………6分 ‎（Ⅱ）（ⅰ）由(Ⅰ)知～，从而 ‎ ………………9分 ‎（ⅱ）由（ⅰ）知，一件产品中质量指标值为于区间（187.8,212.2）的概率为0.6826‎ 依题意知，所以 ………12分 ‎【2014年北京卷（理16）】（本小题13分）.‎ 李明在10场篮球比赛中的投篮情况如下（假设各场比赛互相独立）：‎ 场次 投篮次数 命中次数 场次 投篮次数 命中次数 主场1‎ ‎22‎ ‎12‎ 客场1‎ ‎18‎ ‎8‎ 主场2‎ ‎15‎ ‎12‎ 客场2‎ ‎13‎ ‎12‎ 主场3‎ ‎12‎ ‎8‎ 客场3‎ ‎21‎ ‎7‎ 主场4‎ ‎23‎ ‎8‎ 客场4‎ ‎18‎ ‎15‎ 主场5‎ ‎24‎ ‎20‎ 客场5‎ ‎25‎ ‎12‎ ‎（1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过的概率.‎ ‎（2）从上述比赛中选择一个主场和一个客场，求李明的投篮命中率一场超过，一 ‎ 场不超过的概率.‎ （3） 记是表中10个命中次数的平均数，从上述比赛中随机选择一场，记为李明 ‎ 在这比赛中的命中次数，比较与的大小学科网（只需写出结论）‎ 解（I）根据投篮计数据可以算出李明投篮命中率超过0.6的场次有5场，‎ ‎ 分别是主场2，主场3，主场5，客场2，客场4.‎ 所以在随机选择的一场比赛中，李明的投篮命中率超过0.6的概率是0.5.‎ ‎（Ⅱ）设事件A为“在随机选择的一场主场比赛中李明的投篮命中率超过0.6”，‎ 事件B为“在随机选择的一场客场比赛中李明的投篮命中率超过0.6”，‎ 事件C为“在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6，一场不超过0.6”。‎ 则C=，A,B独立。‎ 根据投篮统计数据，.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 所以，在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过0.6，一场不超过0.6的概率为.‎ ‎（Ⅲ）‎ ‎33.【2014年湖北卷（理20）】计划在某水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水库年入流量(年入流量：一年内上游来水与库区降水之和.单位：亿立方米）都在40以上.其中，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立.‎ (1) 求未来4年中，至多1年的年入流量超过120的概率；‎ (2) 水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量限制，并有如下关系：‎ 年入流量X 发电机最多可运行台数 ‎1‎ ‎2‎ ‎3‎ 若某台发电机运行，则该台年利润为5000万元；若某台发电机未运行，则该台年亏损800万，欲使水电站年利润的均值达到最大，应安装发电机多少台？‎ ‎ 【解析】（Ⅰ）依题意，，，‎ 由二项分布，在未来4年中至多有一年的年入流量超过120的概率为 ‎（Ⅱ）记水电站年总利润为 （1） 安装1台发电机的情形 由于水库年入流量总大于40，故一台发电机运行的概率为1，对应的年利润， ‎ ‎（2）安装2台发电机的情形 依题意，当时，一台发电机运行，此时，因此；当时，两台发电机运行，此时，因此；由此得的分布列如下 Y ‎4200‎ ‎10000‎ P ‎0.2‎ ‎0.8‎ 所以，。‎ ‎（3）安装3台发电机的情形 依题意，当时，一台发电机运行，此时，因此；当时，两台发电机运行，此时，因此；当时，两台发电机运行，此时，因此由此得的分布列如下 Y ‎3400‎ ‎8200‎ ‎15000‎ P ‎0.2‎ ‎0.7‎ ‎0.1‎ 所以，。‎ 综上，欲使水电站年总利润的均值达到最大，应安装发电机2台。‎ 34. ‎【2014年广东卷（理17）】（本小题满分13分）随机观测生产某种零件的某工厂25名工人的日加工零件数（单位：件），获得数据如下：30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36，根据上述数据得到样本的频率分布表如下：‎ 分组 频数 频率 ‎ ‎[25,30 ] 3 0.12‎ ‎(30,35 ] 5 0.20‎ ‎(35,40 ] 8 0.32‎ ‎(40,45 ] n1 f 1 ‎ ‎(45,50 ] n2 f 2 ‎ ‎（1）确定样本频率分布表中和的值；‎ ‎（2）根据上述频率分布表，画出样本频率分布直方图；‎ ‎（3）根据样本频率分布直方图，求在该厂任取4人，至少有1人的日加工零件数落在区间（30,35］的概率。‎ ‎【解析】（1），；‎ ‎ （2）样本日加工零件数 频率 组距 ‎0.016‎ ‎0.024‎ ‎0.04‎ ‎0.056‎ ‎0.064‎ ‎25‎ ‎30‎ ‎35‎ ‎40‎ ‎45‎ ‎50‎ ‎0‎ 频率分布直方图为 ‎（3）根据样本频率分布直方图，每人的日加工零件数落在区间（30,35］的概率0.2，‎ 设所取的4人中，日加工零件数落在区间（30,35］的人数为，则，‎ ‎，‎ 所以4人中，至少有1人的日加工零件数落在区间（30,50］的概率约为0.5904．‎ ‎35.【2014年江西卷（理21）】（本小题满分13分）随机将这2n个连续正整数分成A,B两组，每组n个数，A组最小数为，最大数为；B组最小数为，最大数为，记 （1） 当时，求的分布列和数学期望；‎ （2） 令C表示事件与的取值恰好相等，求事件C发生的概率；‎ ‎（3）对(2)中的事件C, 表示C的对立事件，判断和的大小关系，并说明理由。‎ ‎ ‎ ‎【解析】（1）随机变量的取值所有可能是：2，3，4，5‎ ‎；‎ 的分布列为：‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 所以，的数学期望为 ‎2）事件与的取值恰好相等的基本事件：‎ 共 时，‎ ‎3）因为，所以要比较与的大小，实际上要比较与的大小， 由可知，‎ 当时，‎ 当时，‎ ‎36.【2014年全国新课标Ⅱ（理19）】（本小题满分12分）‎ 某地区2007年至2013年农村居民家庭纯收入y（单位：千元）的数据如下表：‎ 年份 ‎2007‎ ‎2008‎ ‎2009‎ ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ 年份代号t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 人均纯收入y ‎2.9‎ ‎3.3‎ ‎3.6‎ ‎4.4‎ ‎4.8‎ ‎5.2‎ ‎5.9‎ ‎（Ⅰ）求y关于t的线性回归方程；‎ ‎（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.‎ 附：回归直线的斜率和截距的最小二乘法估计公式分别为：‎ ‎，‎ （1） 由所得数据计算得 ‎=（1+2+3+4+5+6+7）=4，‎ ‎=(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3‎ ‎=9+4+1+0+1+4+9=28‎ ‎=(-3) （-1.4）+（-2）（-1）+（-1）（-0.7）+00.1+10.5+20.9+31.6=14，‎ b===0.5‎ a=-b=4.3-0.54=2.3所求回归方程为=0.5t+2.3‎ ‎(Ⅱ)由（Ⅰ ‎）知，b=0.5>0,故2007年至2013年该地区农村居民家庭人均纯收入逐年增加，平均每年增加0.5千元.‎ ‎ ‎ ‎ 将2015年的年份代号t=9代入（1）中的回归方程，得 y=0.5×9+2.3=6.8‎ 故预测该地区2015年农村居民家庭人均纯收入为6.8千元