2006高考数学试题全国II卷理科试题

2006高考数学试题全国II卷理科试题

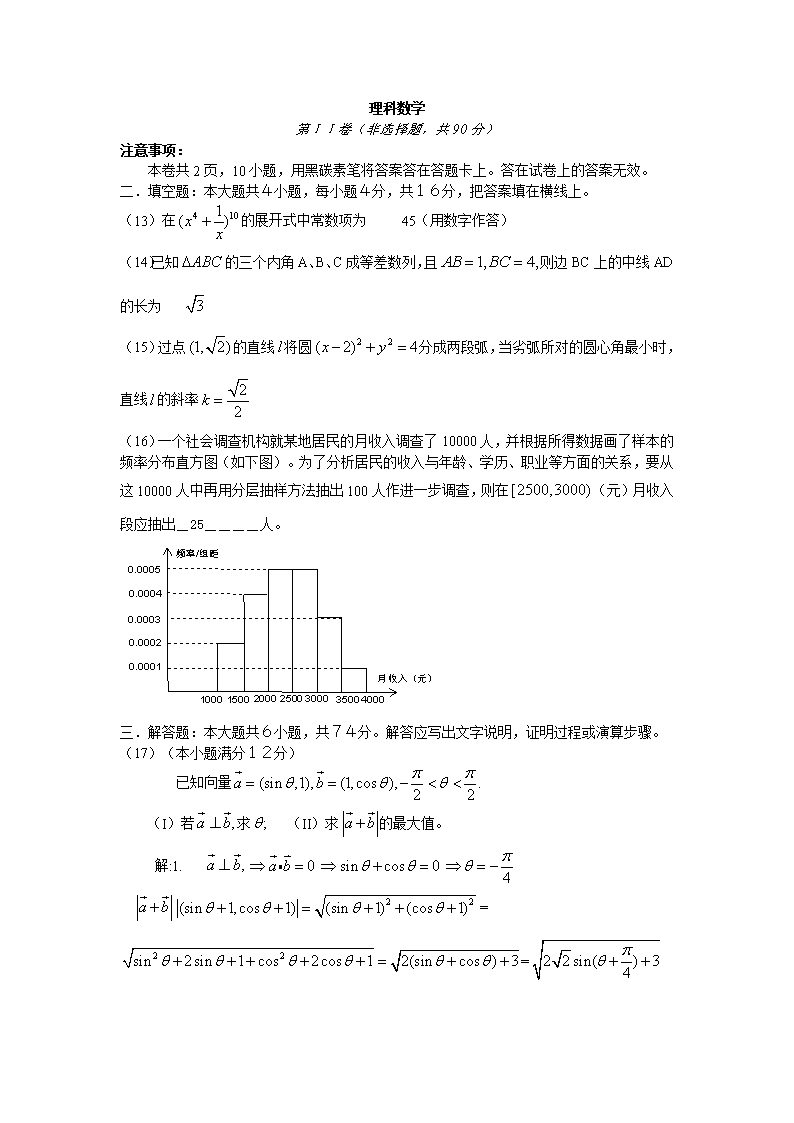
2006高考数学试题全国II卷理科试题 ‎ 本试卷分第Ｉ卷（选择题）和第ＩＩ卷（非选择题）两部分。第Ｉ卷１至２页。第ＩＩ卷３至４页。考试结束后，将本试卷和答题卡一并交回。‎ 第Ｉ卷 注意事项：‎ ‎ １．答题前，考生在答题卡上务必用黑色签字笔将自己的姓名、准考号填写清楚，并贴好条形码。请认真核准条形码上的准考证号、姓名和科目。‎ ‎ ２．每小题选出答案后，用２Ｂ铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效。‎ ‎ 球的表面积公式 ‎ ‎ ‎ 其中Ｒ表示球的半径 ‎ 球的体积公式 ‎ ‎ ‎ 其中Ｒ表示球的半径 ‎ ３．本卷共１２小题，每小题５分，共６０分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ 参考公式 ‎ 如果事件Ａ、Ｂ互斥，那么 ‎ ‎ ‎ 如果事件Ａ、Ｂ相互独立，那么 ‎ ‎ ‎ 如果事件Ａ在一次试验中发生的概率是Ｐ，那么 ‎ 次独立重复试验中恰好发生次的概率是 ‎ ‎ 一．选择题 ‎（1）已知集合，则 (D)‎ ‎ （A）　　　　　　　　　　　　（B）‎ ‎ （C）　　　　　　　（D）‎ ‎（2）函数的最小正周期是(D)‎ ‎ （A）　　　　（B）　　　　（C）　　　　（D）‎ ‎（3）(A)‎ ‎ （A）　　　　（B）　　　　（C）　　　　（D）‎ ‎（4）过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为(A)‎ ‎ （A）　　　　（B）　　　　（C）　　　　（D）‎ ‎（5）已知的顶点B、C在椭圆上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则的周长是 ( C)‎ ‎ （A）　　　　（B）6　　　　（C）　　　　（D）12‎ ‎（6）函数的反函数为(B)‎ ‎ （A）　　　　（B）‎ ‎ （C）　　　　（D）‎ ‎（7）如图，平面平面，与两平面、所成的角分别为和。过A、B分别作两平面交线的垂线，垂足为、则(A)‎ ‎ （A）　　　　（B）‎ ‎ （C）　　　　（D）‎ ‎（8）函数的图像与函数的图像关于原点对称，则的表达式为(D)‎ ‎ （A）　　　　（B）‎ ‎ （C）　　　　（D）‎ ‎（9）已知双曲线的一条渐近线方程为，则双曲线的离心率为(A)‎ ‎ （A）　　　　（B）　　　　（C）　　　　（D）‎ ‎（10）若则(C)‎ ‎ （A）　　　　（B）‎ ‎ （C）　　　　（D）‎ ‎（11）设是等差数列的前项和，若则(A)‎ ‎ （A）　　　　（B）　　　　（C）　　　　（D）‎ ‎（12）函数的最小值为(C)‎ ‎ （A）190　　　　（B）171　　　　（C）90　　　　（D）45‎ 理科数学 第ＩＩ卷（非选择题，共90分）‎ 注意事项：‎ ‎ 本卷共2页，10小题，用黑碳素笔将答案答在答题卡上。答在试卷上的答案无效。‎ 二．填空题：本大题共４小题，每小题４分，共１６分，把答案填在横线上。‎ ‎（13）在的展开式中常数项为 45（用数字作答）‎ ‎（14）已知的三个内角A、B、C成等差数列，且则边BC上的中线AD的长为 ‎ ‎（15）过点的直线将圆分成两段弧，当劣弧所对的圆心角最小时，直线的斜率 ‎（16）一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如下图）。为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在（元）月收入段应抽出＿25＿＿＿＿人。‎ 三．解答题：本大题共６小题，共７４分。解答应写出文字说明，证明过程或演算步骤。‎ ‎（17）（本小题满分１２分）‎ ‎ 已知向量 ‎ （I）若求 （II）求的最大值。‎ 解:1. ‎ ‎==‎ 当=1时有最大值,此时 最大值为 ‎（18）（本小题满分１２分）‎ ‎ 某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意出取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品。‎ ‎ （I）用表示抽检的6件产品中二等品的件数，求的分布列及的数学期望；‎ ‎ （II）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝的概率。‎ 解(1.) ‎ P()= P()=‎ P()= P()=‎ 所以的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 的数学期望E()= ‎ ‎(2)P()=‎ ‎（19）（本小题满分１２分）‎ ‎ 如图，在直三棱柱中，、分别为、的中点。‎ ‎ （I）证明：ED为异面直线与的公垂线；‎ ‎ （II）设求二面角的大小。‎ 提示:1证明与两条异面直线都垂直相交 利用等腰三角形 ‎2 连,由可得为等腰直角三角形,因此在平面内的射影为点所以 ‎（20）（本小题１２分）‎ ‎ 设函数若对所有的都有成立，求实数的取值范围。‎ 提示1 x=0时成立 ‎2 x>0时两边同时除以x ‎（21）（本小题满分为１４分）‎ ‎ 已知抛物线的焦点为F，A、B是热线上的两动点，且过A、B两点分别作抛物线的切线，设其交点为M。‎ ‎ （I）证明为定值；‎ ‎ （II）设的面积为S，写出的表达式，并求S的最小值。‎ 提示1.两向量垂直,定值为0‎ ‎2.三角形面积等于这两个向量模的乘积的一半 ‎（22）（本小题满分１２分）‎ ‎ 设数列的前项和为，且方程 ‎ ‎ ‎ 有一根为 ‎ （I）求 ‎ （II）求的通项公式 提示:1 为方程的根,代入方程可得 将n=1和n=2代入上式可得 ‎ ‎2. ‎