全国高考文科数学试题及解析全国卷
绝密★启用前
2010年普通高等学校招生全国统一考试文科数学(有答案)
本卷分第Ⅰ卷(选择题)和第 Ⅱ卷(非选择题)两部分,第Ⅰ卷第1页至第2页,第 Ⅱ卷第3页至第4页。考试结束后,将本试卷和答题Ⅰ、Ⅱ交回,全卷满分150分,考试时间120分钟。
第Ⅰ卷 (选择题 共50分)
选择题:本大题共10小题,每小题5分,共50分。在,每小题给出的四个选项中,
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4πR2
如果事件A、B相互独立,那么
P(A-B)=P(A)-P(B)
一. 选择题
(1)设全集U={|<6 },集合A={1,3}。B={3,5},则CU()=( )
(A){1,4} (B){1,5}
(C){2,4} (D){2,4}
(2)不等式的解集为( )
(A){X|-2
3} (D){X∣X>3}
(3)已知sina=,则cos(π-2a)=
(A) (B) (C) (D)
(4)函数y=1+ln(x-1)(x>1)的反函数是
(A)y=ex+1-1(x>0) (B) y=ex+1+1(x>0)
(C)y=ex+1-1 (x∈R) (D) y=ex+1+1 (x∈R)
(5) 若变量x,y满足约束条件,则z=2x+y的最大值为
(A) 1 (B) 2 (C) 3 (D)4[
来
(6)如果等差数列{an} 中,a3+a4+a5=12,那么 a1+a2+……+an=
(A) 14 (B) 21 (C) 28 (D)35
(7)若曲线y=在点(0.b)处的切线方程式=0,则
(A), (B),
(C) , (D)
(8)已知三棱锥中,底面ABC为变长等于2的等边三角形,SA垂直于底面ABC,SA=3,那么直线AB与平面SBC所成的角 的正弦值为
(A) (B) (C) (D)
(9)将标号为1,2,3,4,5,6的6张卡放入3个不同的信封中,若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的放法共有
(A) 12种 (B) 18种 (C) 36种 (D)54种
(10)△ABC中,点D在边AB上,CD平分∠ABC,若=a,=b,∣a∣=1,
∣b∣=2,则=
(A)a+b (B)a+b (C)a+b (D)a+b
(11)与正方体ABCD-A1B1C1D1的三条棱AB、CC1D所在直线的距离相等的点
(A)有且只有1个 (B)有且只有2个 (C)有且只有3个 (D)有无数个
(12)已知椭圆C:+=1(a>b>0)的离心率为,过右焦点F且斜率k(k>0)的直线与C相交于A、B亮点,若=3,则k=
(A)1 (B) (C) (D)2
二.填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡上。
(13)已知a是第二象限的角tana=,则cos a=___________。
(14)9的展开式中x3 的系数是__________。
(15)已知抛物线C:y2 =2px(p>0)的准线为l,过M(1,0)且斜率为的直线与l相交于A,与C的一个交点为B,若=则p等于_________.
16 已知球O的半径为4,圆M与圆N为该球的两个小圈,AB为圆M与圆M的公共弦,AB=4,若OM=ON=3,则两圆圆心的距离MN=________________.
三.解答题:本大题共6小题,共70分,解答应写出说明,证明过程或演算步骤。
(17)(本小题满分10分)
三角形ABC中,D为边BC上的一点,BD=33,sinB=,cos∠ADC=.求AD.
(18)(本小题满分12分)
已知{an}是各项均为正数的等比例数列,且
a1+a2=2().a2+a3+a4=64()
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=(an+)2,求数列{bn}的前N项和Tn.[来源:Z§
xx§k.Com]
(19)(本小题满分12分)
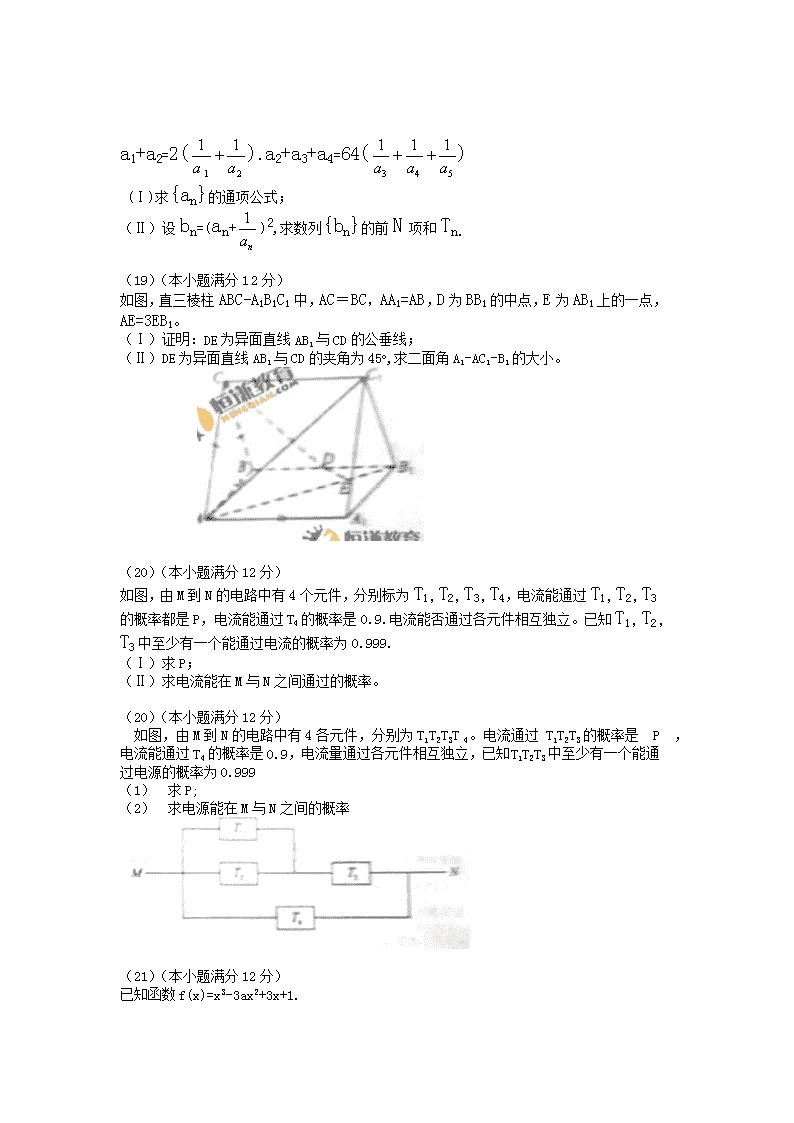
如图,直三棱柱ABC-A1B1C1中,AC=BC,AA1=AB,D为BB1的中点,E为AB1上的一点,AE=3EB1。
(Ⅰ)证明:DE为异面直线AB1与CD的公垂线;
(Ⅱ)DE为异面直线AB1与CD的夹角为45o,求二面角A1-AC1-B1的大小。
[来源:Zxxk.Com]
(20)(本小题满分12分)
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是P,电流能通过T4的概率是0.9.电流能否通过各元件相互独立。已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
(Ⅰ)求P;
(Ⅱ)求电流能在M与N之间通过的概率。
(20)(本小题满分12分)
如图,由M到N的电路中有4各元件,分别为T1T2T3T 4。电流通过 T1T2T3的概率是 P ,电流能通过T 4的概率是0.9,电流量通过各元件相互独立,已知 T1T2T3中至少有一个能通过电源的概率为0.999
(1) 求P;
(2) 求电源能在M与N之间的概率
(21)(本小题满分12分)[来源:学#科#网Z#X#X#K]
已知函数f(x)=x3-3ax2+3x+1.
(1) 设 a=2 ,求f(x)的单调区间;
(2) 设f(x)在区间(2,3)中至少有一个极致点,求 a 的取值范围
(22)(本小题满分12分)
(21)(本小题满分12分)
已知函数
(Ⅰ)设,求的单调区间
(Ⅱ)设在区间(2、3)中至少有一个极值点,求a的取值范围
(22)(本小题满分12分)
已知斜率为1的直线与双曲线相交于B、D两点,且BD的中点为
(Ⅰ)求的离心率;
(Ⅱ)设的右顶点为A,右焦点为F, 证明:过A、B、D三点的圆与轴相切。
2010年高校招生全国统一考试文数(全国2卷)参考答案