- 2021-05-13 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考复习专题圆锥曲线技巧总结
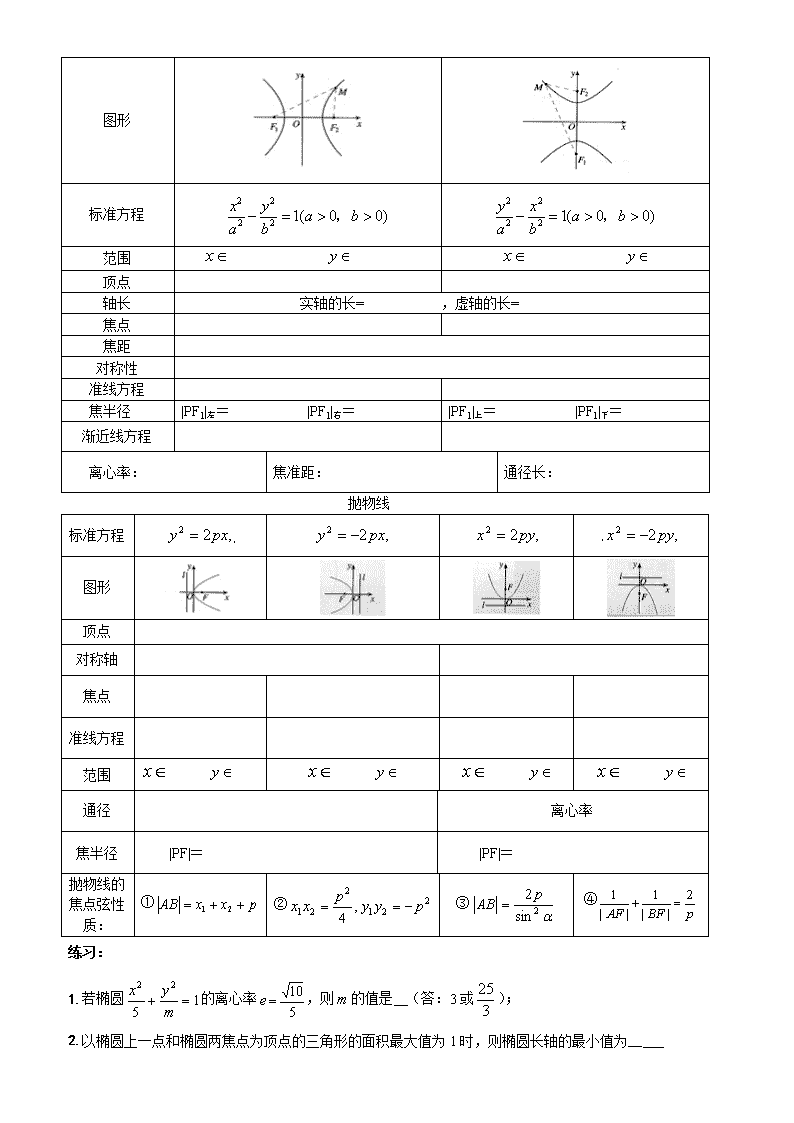
【高考总复习】圆锥曲线概念方法技巧总结 一.圆锥曲线的定义: 定义中要重视“括号”内的限制条件: 椭圆中,与两个定点F,F的距离的和等于常数,且此常数一定要大于,当常数等于时,轨迹是线段FF,当常数小于时,无轨迹; 双曲线中,与两定点F,F的距离的差的绝对值等于常数,且此常数一定要小于|FF|,定义中的“绝对值”与<|FF|不可忽视。若=|FF|,则轨迹是以F,F为端点的两条射线,若﹥|FF|,则轨迹不存在。若去掉定义中的绝对值则轨迹仅表示双曲线的一支。 练习: 1.已知定点,在满足下列条件的平面上动点P的轨迹中是椭圆的是(答:C); A. B. C. D. 2.方程表示的曲线是_____(答:双曲线的左支) 3.已知点及抛物线上一动点P(x,y),则y+|PQ|的最小值是_____(答:2) 二.圆锥曲线的标准方程(标准方程是指中心(顶点)在原点,坐标轴为对称轴时的标准位置的方程): (1)椭圆:焦点在轴上时()(参数方程,其中为参数),焦点在轴上时=1()。方程表示椭圆的充要条件是什么?(ABC≠0,且A,B,C同号,A≠B)。 (2)双曲线:焦点在轴上: =1,焦点在轴上:=1()。方程表示双曲线的充要条件是什么?(ABC≠0,且A,B异号)。 (3)抛物线:开口向右时,开口向左时,开口向上时,开口向下时。 练习: 1.已知方程表示椭圆,则的取值范围为____(答:); 2.若,且,则的最大值是____,的最小值是___(答:) 3.双曲线的离心率等于,且与椭圆有公共焦点,则该双曲线的方程_______ 4.设中心在坐标原点,焦点、在坐标轴上,离心率的双曲线C过点,则C的方程为_______(答:) 5.已知方程表示焦点在y轴上的椭圆,则m的取值范围是__ 三.圆锥曲线焦点位置的判断(首先化成标准方程,然后再判断): (1)椭圆:由,分母的大小决定,焦点在分母大的坐标轴上。 (2)双曲线:由,项系数的正负决定,焦点在系数为正的坐标轴上; (3)抛物线:焦点在一次项的坐标轴上,一次项的符号决定开口方向。 特别提醒:(1)在求解椭圆、双曲线问题时,首先要判断焦点位置,焦点F,F的位置,是椭圆、双曲线的定位条件,它决定椭圆、双曲线标准方程的类型,而方程中的两个参数,确定椭圆、双曲线的形状和大小,是椭圆、双曲线的定形条件;在求解抛物线问题时,首先要判断开口方向;(2)在椭圆中,最大,,在双曲线中,最大,。 四.圆锥曲线的几何性质: 椭圆的图像和性质 焦点的位置 焦点在轴上 焦点在轴上 图形 标准方程 范围 顶点 轴长 长轴的长= , 短轴的长= 焦点 焦距 对称性 准线方程 焦半径 |PF1|左= |PF1|右= |PF1|上= |PF1|下= 离心率: 焦准距: 通径长: 双曲线的图像和性质 焦点的位置 焦点在轴上 焦点在轴上 图形 标准方程 范围 顶点 轴长 实轴的长= ,虚轴的长= 焦点 焦距 对称性 准线方程 焦半径 |PF1|左= |PF1|右= |PF1|上= |PF1|下= 渐近线方程 离心率: 焦准距: 通径长: 抛物线 标准方程 图形 顶点 对称轴 焦点 准线方程 范围 通径 离心率 焦半径 |PF|= |PF|= 抛物线的焦点弦性质: ① ② ③ ④ 练习: 1.若椭圆的离心率,则的值是__(答:3或); 2.以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为__ 3.双曲线的渐近线方程是,则该双曲线的离心率等于______(答:或); 4.双曲线的离心率为,则= (答:4或); 5.设双曲线(a>0,b>0)中,离心率e∈[,2],则两条渐近线夹角θ的取值范围是___(答:); 6.设,则抛物线的焦点坐标为________(答:); 五、点和椭圆()的关系:(1)点在椭圆外;(2)点在椭圆上=1;(3)点在椭圆内 六.直线与圆锥曲线的位置关系: (1)相交:直线与椭圆相交; 直线与双曲线相交,但直线与双曲线相交不一定有,当直线与双曲线的渐近线平行时,直线与双曲线相交且只有一个交点,故是直线与双曲线相交的充分条件,但不是必要条件;直线与抛物线相交,但直线与抛物线相交不一定有,当直线与抛物线的对称轴平行时,直线与抛物线相交且只有一个交点,故也仅是直线与抛物线相交的充分条件,但不是必要条件。如 (2)相切:直线与椭圆相切;直线与双曲线相切;直线与抛物线相切; (3)相离:直线与椭圆相离;直线与双曲线相离;直线与抛物线相离。 特别提醒:(1)直线与双曲线、抛物线只有一个公共点时的位置关系有两种情形:相切和相交。如果直线与双曲线的渐近线平行时,直线与双曲线相交,但只有一个交点;如果直线与抛物线的轴平行时,直线与抛物线相交,也只有一个交点;(2)过双曲线=1外一点的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;(3)过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和一条平行于对称轴的直线. 练习: 1.若直线y=kx+2与双曲线x2-y2=6的右支有两个不同的交点,则k的取值范围是_______ 2.直线y―kx―1=0与椭圆恒有公共点,则m的取值范围是_______ 3.过双曲线的右焦点直线交双曲线于A、B两点,若│AB︱=4,则这样的直线有_____条 4.过点作直线与抛物线只有一个公共点,这样的直线有______(答:2); 5.过点(0,2)与双曲线有且仅有一个公共点的直线的斜率的取值范围为______ 6.过双曲线的右焦点作直线交双曲线于A、B两点,若4,则满足条件的直线有____ 7.对于抛物线C:,我们称满足的点在抛物线的内部,若点在抛物线的内部,则直线:与抛物线C的位置关系是_______(答:相离); 8.过抛物线的焦点作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是、,则_______(答:1); 9.设双曲线的右焦点为,右准线为,设某直线交其左支、右支和右准线分别于,则和的大小关系为___________(填大于、小于或等于) (答:等于); 10.求椭圆上的点到直线的最短距离(答:); 11.直线与双曲线交于、两点。①当为何值时,、分别在双曲线的两支上?②当为何值时,以AB为直径的圆过坐标原点?(答:①;②); 七、焦半径(圆锥曲线上的点P到焦点F的距离)的计算方法:利用圆锥曲线的第二定义,转化到相应准线的距离,即焦半径,其中表示P到与F所对应的准线的距离。 练习: 1.已知椭圆上一点P到椭圆左焦点的距离为3,则点P到右准线的距离为____(答:); 2.已知抛物线方程为,若抛物线上一点到轴的距离等于5,则它到抛物线的焦点的距离等于____; 3.若该抛物线上的点到焦点的距离是4,则点的坐标为_____(答:); 4.点P在椭圆上,它到左焦点的距离是它到右焦点距离的两倍,则点P的横坐标为_______ 5.抛物线上的两点A、B到焦点的距离和是5,则线段AB的中点到轴的距离为______ 6.椭圆内有一点,F为右焦点,在椭圆上有一点M,使 之值最小,则点M的坐标为_______(答:); 八、焦点三角形(椭圆或双曲线上的一点与两焦点所构成的三角形)问题:常利用第一定义和正弦、余弦定理求解。设椭圆或双曲线上的一点到两焦点的距离分别为,焦点的面积为,则在椭圆中, ,当即为短轴端点时,的最大值为bc;对于双曲线的焦点三角形有: 。 练习: 1.短轴长为,离心率的椭圆的两焦点为、,过作直线交椭圆于A、B两点,则的周长为________(答:6); 2.设P是等轴双曲线右支上一点,F1、F2是左右焦点,若,|PF1|=6,则该双曲线的方程为 (答:); 3.椭圆的焦点为F1、F2,点P为椭圆上的动点,当·<0时,点P的横坐标的取值范围是 (答:); 4.双曲线的虚轴长为4,离心率e=,F1、F2是它的左右焦点,若过F1的直线与双曲线的左支交于A、B两点,且是与等差中项,则=__________(答:); 5.已知双曲线的离心率为2,F1、F2是左右焦点,P为双曲线上一点,且,.求该双曲线的标准方程(答:); 九、抛物线中与焦点弦有关的一些几何图形的性质: (1)以过焦点的弦为直径的圆和准线相切;(2)设AB为焦点弦, M为准线与x轴的交点,则∠AMF=∠BMF;(3)设AB为焦点弦,A、B在准线上的射影分别为A,B,若P为AB的中点,则PA⊥PB;(4)若AO的延长线交准线于C,则BC平行于x轴,反之,若过B点平行于x轴的直线交准线于C点,则A,O,C三点共线。 十、弦长公式:若直线与圆锥曲线相交于两点A、B,且分别为A、B的横坐标,则 =,若分别为A、B的纵坐标,则=,若弦AB所在直线方程设为,则=。特别地,焦点弦(过焦点的弦):焦点弦的弦长的计算,一般不用弦长公式计算,而是将焦点弦转化为两条焦半径之和后,利用第二定义求解。 练习: 1.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,若x1+x2=6,那么|AB|等于_______ 2.过抛物线焦点的直线交抛物线于A、B两点,已知|AB|=10,O为坐标原点,则ΔABC重心的横坐标为_______(答:3); 十一、圆锥曲线的中点弦问题:遇到中点弦问题常用“韦达定理”或“点差法”求解。在椭圆中,以为中点的弦所在直线的斜率k=-;在双曲线中,以为中点的弦所在直线的斜率k=;在抛物线中,以为中点的弦所在直线的斜率k=。 练习: 1.如果椭圆弦被点A(4,2)平分,那么这条弦所在的直线方程是 (答:); 2.已知直线y=-x+1与椭圆相交于A、B两点,且线段AB的中点在直线L:x-2y=0上,则此椭圆的离心率为_______(答:); 特别提醒:因为是直线与圆锥曲线相交于两点的必要条件,故在求解有关弦长、对称问题时,务必别忘了检验! 十二.你了解下列结论吗? (1)双曲线的渐近线方程为; (2)以为渐近线(即与双曲线共渐近线)的双曲线方程为为参数,≠0)。 (3)中心在原点,坐标轴为对称轴的椭圆、双曲线方程可设为; (4)椭圆、双曲线的通径(过焦点且垂直于对称轴的弦)为,焦准距(焦点到相应准线的距离)为,抛物线的通径为,焦准距为; (5)通径是所有焦点弦(过焦点的弦)中最短的弦; (6)若抛物线的焦点弦为AB,,则①;② (7)若OA、OB是过抛物线顶点O的两条互相垂直的弦,则直线AB恒经过定点 13.动点轨迹方程: (1)求轨迹方程的步骤:建系、设点、列式、化简、确定点的范围; (2)求轨迹方程的常用方法: ①直接法:直接利用条件建立之间的关系;如已知动点P到定点F(1,0)和直线的距离之和等于4,求P的轨迹方程.(答:或); ②待定系数法:已知所求曲线的类型,求曲线方程――先根据条件设出所求曲线的方程,再由条件确定其待定系数。如线段AB过x轴正半轴上一点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线,则此抛物线方程为 (答:); ③定义法:先根据条件得出动点的轨迹是某种已知曲线,再由曲线的定义直接写出动点的轨迹方程;如(1)由动点P向圆作两条切线PA、PB,切点分别为A、B,∠APB=600,则动点P的轨迹方程为 (答:);(2)点M与点F(4,0)的距离比它到直线的距离小于1,则点M的轨迹方程是_______ (答:);(3) 一动圆与两圆⊙M:和⊙N:都外切,则动圆圆心的轨迹为 (答:双曲线的一支); ④代入转移法:动点依赖于另一动点的变化而变化,并且又在某已知曲线上,则可先用的代数式表示,再将代入已知曲线得要求的轨迹方程;如动点P是抛物线上任一点,定点为,点M分所成的比为2,则M的轨迹方程为__________(答:); ⑤参数法:当动点坐标之间的关系不易直接找到,也没有相关动点可用时,可考虑将均用一中间变量(参数)表示,得参数方程,再消去参数得普通方程)。如(1)AB是圆O的直径,且|AB|=2a,M为圆上一动点,作MN⊥AB,垂足为N,在OM上取点,使,求点的轨迹。(答:);(2)若点在圆上运动,则点的轨迹方程是____(答:);(3)过抛物线的焦点F作直线交抛物线于A、B两点,则弦AB的中点M的轨迹方程是________(答:); ②曲线与曲线方程、轨迹与轨迹方程是两个不同的概念,寻求轨迹或轨迹方程时应注意轨迹上特殊点对轨迹的“完备性与纯粹性”的影响. ③在与圆锥曲线相关的综合题中,常借助于“平面几何性质”数形结合(如角平分线的双重身份――对称性、利用到角公式)、“方程与函数性质”化解析几何问题为代数问题、“分类讨论思想”化整为零分化处理、“求值构造等式、求变量范围构造不等关系”等等. ④如果在一条直线上出现“三个或三个以上的点”,那么可选择应用“斜率或向量”为桥梁转化. 圆锥曲线常见题型及解题思路方法。 1. 求圆锥曲线的标准方程 先判断焦点的位置,设出相应圆锥曲线的方程,再根据已知条件和圆锥曲线的性质列方程(组)(如求椭圆方程,就是根据条件和性质列出关于a、b、c的方程组),求出待定参数。 2. 求椭圆(或双曲线)的离心率或离心率的取值范围 求离心率就是根据条件和圆锥曲线的性质,寻找a、b、c之间的等量关系,求出的值。在椭圆中,有:;在双曲线中,有:。能求出,也就求得了离心率。在双曲线中,还要注意渐近线与离心率的关系。 求离心率的取值范围就是根据条件和圆锥曲线的性质寻找a、b、c之间的不等关系。关于不等式的来源,通常是依据已知不等式,同时还要注意圆锥曲线中 几个常用的不等关系:①圆锥曲线上点的坐标的范围;②在椭圆中,有,(其中B为短轴的端点,P为椭圆上任一点);③在双曲线中,有(其中F为焦点, P为双曲线上任一点,A是同一支双曲线的顶点)。 解这类问题时,要尽可能地结合图形,依据定义,多从几何角度思考问题。如果涉及直线与圆锥曲线位置关系问题,还要联立方程,用坐标法找关系。 3. 在圆锥曲线中判断点与圆的位置关系 除常规方法外(比较点到圆心的距离与半径的大小),通常用向量法。例如,已知直线与圆锥曲线交于A、B两点,要判断点P与以AB为直径的圆的位置关系,只需确定的大小,通过计算,确定其符号。 4. 证明定点,定值,定直线问题 可先取参数的特殊值(或图形的特殊位置),对定点,定值,定直线进行探求,然后证明当参数变化时,结论成立。 证明直线过定点,有两种思路:①求出满足条件的动直线方程(只含一个参数),再根据方程求出定点;② 先探求定点,再设出要证明的定点的坐标(如设动直线与x轴交于点),把坐标表示出来,表示式中,往往会含有(或 ),用所求得的结果代入,就可得出坐标为定值。 证明定点、定值、定直线问题,还可利用圆锥曲线中定点、定值、定直线的性质,将问题进行转化。 5. 直线与圆锥曲线的位置关系问题 这类问题是平面解析几何中的重点问题,常涉及直线和圆锥曲线交点的判断,弦长,面积,对称,共线等问题 处理问题的基本方法有两种: (1)联立方程法:解题步骤是:先设交点 ,再设直线方程,联立直线方程与圆锥曲线方程构成方程组,消元,求,(或 ),令(如果直线经过曲线内的点,可以省去这一步),再根据问题的要求或求距离,或求弦长,或求点的坐标,或求面积等。 (2)点差法:设交点为及AB的中点,将A、B两点的坐标代人圆锥曲线方程,作差变形,可得:,即,再由题设条件,求中点坐标,根据问题的条件和要求列式。 值得注意的是,用联立方程法,设直线方程时,为简化运算,可采用这种的策略,若直线过轴上的定点,则直线方程可设为(此直线不包括轴),联立方程,消去,得到关于的方程,求出备用。有时,还要根据,求出。若直线过轴上的定点,则直线方程可设为(此直线不包括轴),联立方程,消去y。 对于直线,无特殊交代时,通常注意分两种情况:①直线的斜率存在,消元后,注意;②直线的斜率不存在,即直线为。 在涉及到弦的中点及斜率时,求参数(如直线的斜率k)的取值范围,通常采用点差法。 6. 最值问题 这类问题是从动态角度研究解析几何中的有关问题,往往涉及求弦长(或距离)、面积、坐标(或截距)、向量的模(或数量积)、参数等的最大(小)值。 其解法是:设变量,建立目标函数。处理的方法有: (1)利用基本不等式; (2)考察函数的单调性; (3)利用判别式法。 在目标函数的变形上有一定的技巧,关于弦长,面积表达式的变形,常用到移入根号,分离常数,换元等方法,把目标函数转化为双勾函数的形式,或用基本不等式,或利用函数的单调性求最值。求坐标的最值时,可构造一个一元二次方程,利用。 7. 求参数的取值范围问题 这类问题主要是根据条件建立关于参变量的不等式,或者把所求参数转化关于某个变量的函数,通过解不等式或求函数的值域来求参数的取值范围。 具体解法如下: (1)结合定义利用图形中几何量之间的大小关系。 (2)不等式(组)求解法:利用题意结合图形列出所讨论的参数适合的不等式(组),通过解不等式组得出参数的变化范围。不等式的来源常有以下途径:①已知不等式(含基本不等式);②直线与圆锥曲线相交时,有 ;③点与圆锥曲线(以椭圆最为多见)的位置关系;④圆锥曲线(特别是椭圆)上点的坐标的范围。 (3)函数值域求解法:把所讨论的参数作为一个函数,用一个适当的参数作为自变量来表示这个函数,通过讨论函数的值域来求参数的变化范围。 (4)利用基本不等式:基本不等式的应用,往往需要创造条件,并进行巧妙的构思。 (5)结合参数方程,利用三角函数的有界性。圆、椭圆的参数方程,它们的一个共同特点是均含有三角式。因此,它们的应用价值在于:① 通过参数θ简明地表示曲线上点的坐标;② 利用三角函数的有界性及其变形公式来帮助求解诸如最值、范围等问题。 (6)构造一个二次方程,利用判别式D³0。 8. 求动点的轨迹方程 求动点的轨迹方程是解析几何中两类基本问题之一,即根据动点所满足的条件,求动点的坐标之间的关系式。最基本的方法是直接法,步骤是:建系设点条件立式坐标代换化简方程查漏除杂。此外还有定义法(主要是利用圆锥曲线的定义),相关点法,参数法,几何法等。在涉及直线、圆的轨迹问题时,常从几何角度去探求动点满足的关系,选用几何法;如果题目没有直接给出动点所满足的条件,而是给出了与动点相关的点所满足的条件,先设动点坐标为,再把相关点的坐标用动点的坐标来表示,根据相关点的条件列式,此即为相关点法;参数法是求轨迹方程常用的方法,合理引入参数(通常是相关点的坐标)列式,消去参数得到关于的方程,要求所列方程的数目要比引入的参数多一个,才能消去所有参数。 三. 圆锥曲线问题中的条件及要求与韦达定理之间的联系举例: 解决圆锥曲线问题的基本方法是坐标法,这就需要把问题的条件转化为坐标之间的关系,而把问题的条件和要求用坐标表示,特别是用或来表示,往往又是打通问题思路的关键。以下是问题中一些条件的坐标表示: 设斜率为的直线与圆锥曲线交于两点,联立方程,可求出,以及。 (1)弦的中点: 弦AB的中点坐标可表示为 (2)弦的垂直平分线过定点或: 弦的垂直平分线方程为:。 弦的垂直平分线过定点,则有: (3)点与以为直径的圆的位置关系, 判断的符号: ,, 。 其中 (4)垂直问题: 如,则有: (5)A、B两点关于直线对称: ,(其中k为直线AB的斜率) 关于圆锥曲线上两点关于某条直线对称的问题,一般涉及到弦的斜率和中点,所以常采用“点差法”,用点差法处理问题时,对于不同的圆锥曲线,有不同的表示方法:当圆锥曲线分别为椭圆、双曲线、抛物线时,k的表示式有以下三种形式: (椭圆); (双曲线);(抛物线) (6)弦长问题: 当直线 时: 当直线时: (7)三角形的面积: M N A B ①; (d是点到直线AB的距离) ②或, 其中M、N为x轴上两定点,为定长。 (8)三点共线问题: 遇三点共线问题,常利用斜率相等列方程。 设,若共线,则 利用直线方程将换成(或将换成),通分后令分子 为0,可使所得方程中仅含有(或仅含有)。 (9)为正三角形: 点C在的垂直平分线上,且满足,其中M为的中点。由点C在的垂直平分线上可得: 又,, 这样就把问题与韦达定理联系起来了。 (10)A、B与C、D四点共圆: 当A、C、B、D四点共圆时,其圆心是线段AB的垂直平分线与线段CD的垂直平分线的交点G,且满足|GA|=|GC|。线段AB的垂直平分线方程为, 若CD垂直平分AB, 则圆心G是CD的中点,且有.查看更多